Abstract
A correct Network Segmentation (NS) is necessary to perform proper maintenance activities in water distribution networks (WDN). For this, usually, isolation valves are allocating near the ends of pipes, blocking the flow of water. However, the allocation of valves increases costs substantially for the water supply companies. Additionally, other criteria should be taking account to analyze the benefits of the valves allocation. Thus, the problem is to define an alternative of NS which shows a good compromise in these different criteria. Moreover, usually, in this type of decision, there is more than one decision-maker involved, who can have different viewpoints. Therefore, this paper presents a model to support group decision-making, based on a multi-criteria method, in order to support the decision making procedure in the NS problem. As result, the model is able to find a solution that shows the best compromise regarding the benefits, costs, and the decision makers' preferences.
Keywords
Maintenance activities; Network segmentation; Group decision-making; Multi-criteria approach; PROMETHEE GDSS method
1 Introduction
In some countries, there is a deficiency in the management of potable water use by the sanitation companies and it generates undesirable wastage such as physical and economic losses, which are due to, in some cases, the lack of planning of the water system maintenance (Trojan & Morais, 2012aTrojan, F., & Morais, D. C. (2012a). Using Electre TRI to support maintenance of water distribution networks. Pesquisa Operacional, 32(2), 423-442. http://dx.doi.org/10.1590/S0101-74382012005000013.
http://dx.doi.org/10.1590/S0101-74382012...
). In this scenario, the supply of water has become of great concern worldwide because it is a scarce resource in many regions. For this reason, many research studies are being undertaken on ways to tackle and mitigate these problems (Fontana & Morais, 2013Fontana, M. E., & Morais, D. C. (2013). Using PROMETHEE V to select alternatives so as to rehabilitate water supply network with detected leaks. Water Resources Management, 27(11), 4021-4037. http://dx.doi.org/10.1007/s11269-013-0393-1.
http://dx.doi.org/10.1007/s11269-013-039...
).
In this context, to conduct a proper maintenance activity (preventive and corrective) will be necessary to interrupt the water distribution networks (WDN). In other words, it is needed an insulation of pipes (Giustolisi et al., 2008Giustolisi, O., Kapelan, Z., & Savic, D. (2008). Extended period simulation analysis considering valve shutdowns. Journal of Water Resources Planning and Management, 134(6), 527-537. http://dx.doi.org/10.1061/(ASCE)0733-9496(2008)134:6(527).
http://dx.doi.org/10.1061/(ASCE)0733-949...
). For this, WDN segmentation, or sectorization, consists of dividing a water system into sectors (segments) with an independent water supply (Di Nardo et al., 2014Di Nardo, A., Di Natale, M., Santonastaso, G. F., Tzatchkov, V. G., & Alcocer-Yamanaka, V. H. (2014). Water network sectorization based on genetic algorithm and minimum dissipated power paths. Water Science and Technology: Water Supply, 13(4), 951-957. http://dx.doi.org/10.2166/ws.2013.059.
http://dx.doi.org/10.2166/ws.2013.059...
). In this way, WDN usually are made up of a large number of network segments, where a smallest portion from WDN can be isolated by operating the valves (Walski, 1993aWalski, T. M. (1993a). Practical aspects of providing reliability in water distribution systems. Reliability Engineering & System Safety, 42(1), 13-19. http://dx.doi.org/10.1016/0951-8320(93)90050-9.
http://dx.doi.org/10.1016/0951-8320(93)9...
).
In this sense, a valve is defined as a mechanical device by which the flow of fluid may be started, stopped, or regulated by a movable part that opens or obstructs passage (Ozger & Mays, 2004Ozger, S., & Mays, L. W. (2004). Optimal location of isolation valves in water distribution systems: a reliability/optimization approach. In L. W. Mays (Ed.), Water resource systems management tools (chap. 7.1-7.24). New York: McGraw-Hill Education.). Recent concerns regarding protecting, identifying and isolating of subsystems of WDN have led to the realization of the importance of valves in these systems (Jun & Loganathan, 2007Jun, H., & Loganathan, G. V. (2007). Valve-controlled segments in water distribution systems. Journal of Water Resources Planning and Management, 133(2), 145-155. http://dx.doi.org/10.1061/(ASCE)0733-9496(2007)133:2(145).
http://dx.doi.org/10.1061/(ASCE)0733-949...
). Thus, valves are the key for a reliable water distribution system (Walski, 1993bWalski, T. M. (1993b). Water Distribution Valve Topology for reliability analysis. Reliability Engineering & System Safety, 42(1), 1-21. http://dx.doi.org/10.1016/0951-8320(93)90051-Y.
http://dx.doi.org/10.1016/0951-8320(93)9...
). They determine the extent of isolation when a portion of the network need repair, inspection, or maintenance (Ozger & Mays, 2004Ozger, S., & Mays, L. W. (2004). Optimal location of isolation valves in water distribution systems: a reliability/optimization approach. In L. W. Mays (Ed.), Water resource systems management tools (chap. 7.1-7.24). New York: McGraw-Hill Education.), and, consequently, the consequences associated due to the reduction of the available water in the system or the total interruption of water supply.
Valves are typically located around junctions in a WDN. In Brazil, there is a standard, NBR 12218, which says it is necessary to provide a valve in the secondary pipes (that directly supply units) near the point of attachment to the main pipes (pipes that supply the secondary) (Associação Brasileira de Normas Técnicas, 1994Associação Brasileira de Normas Técnicas. (1994). NBR 12218/1994: project of water distribution network for public supply. Rio de Janeiro: ABNT. Retrieved in 5 April 2012, from http://www.abnt.org.br/
http://www.abnt.org.br/...
). Moreover, it is usual to install one less valve than the number of pipes at a junction, i.e., the rule “N-1” valves. However, an ideal system will require two valves for each pipe located at its ends, ie., the rule “N” valves (Jun & Loganathan, 2007Jun, H., & Loganathan, G. V. (2007). Valve-controlled segments in water distribution systems. Journal of Water Resources Planning and Management, 133(2), 145-155. http://dx.doi.org/10.1061/(ASCE)0733-9496(2007)133:2(145).
http://dx.doi.org/10.1061/(ASCE)0733-949...
).
However, the allocation of valves substantially increases the costs to water supply companies, both the cost of deployment of the valves and the cost for their maintenance (Heller & Pádua 2006Heller, L., & Pádua, V. L. (2006). Water supply for human consumption. Belo Horizonte: UFMG.). Thus, the optimal segmentation for WDNs needs to be performed versus the minimization of the cost of installed devices (Giustolisi & Ridolfi, 2014Giustolisi, O., & Ridolfi, L. (2014). New modularity-based approach to segmentation of water distribution networks. Journal of Hydraulic Engineering, 140(10), 04014049. http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000916.
http://dx.doi.org/10.1061/(ASCE)HY.1943-...
). Moreover, the valves that remain in the same position for long periods make their operation difficult unless they are “handled” on occasion (Mays, 2000Mays, L. W. (Org.). (2000). Water distribution systems handbook. New York: McGraw-Hill.). Nevertheless, it requires an extraordinary effort of the operators to close and (later) open valves. This if all the valves are found, since the omission of their location, in the register of the network, is common, as well as, there is a difficulty to accessing the valves due to the size of the protective box. To avoid these problems, Water Companies should make rational use of the valves in the network (Heller & Pádua, 2006Heller, L., & Pádua, V. L. (2006). Water supply for human consumption. Belo Horizonte: UFMG.). Therefore, the WDN segmentation presents a difficult trade-off between the costs involved, especially the implementation and maintenance of valves, and the benefits generated to users (Fontana & Morais, 2015Fontana, M. E., & Morais, D. C. (2015). Segmentation model for water distribution networks based on the characteristics of consumer units. Production, 25(1), 143-156. http://dx.doi.org/10.1590/S0103-65132013005000071.
http://dx.doi.org/10.1590/S0103-65132013...
).
Some models to optimize the location of isolation valves in WDN can be found in the literature. Due to the complex nature of the problem, many authors use heuristic optimization techniques to solve this type of problem, such as Creaco et al. (2010)Creaco, E., Franchini, M., & Alvisi, S. (2010). Optimal placement of isolation valves in water distribution systems based on valve cost and weighted average demand shortfall. Water Resources Management, 24(15), 4317-4338. http://dx.doi.org/10.1007/s11269-010-9661-5.
http://dx.doi.org/10.1007/s11269-010-966...
, Giustolisi & Savic (2010)Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530.
http://dx.doi.org/10.1080/15730620903287...
and Ozger & Mays (2004)Ozger, S., & Mays, L. W. (2004). Optimal location of isolation valves in water distribution systems: a reliability/optimization approach. In L. W. Mays (Ed.), Water resource systems management tools (chap. 7.1-7.24). New York: McGraw-Hill Education.. Ozger & Mays (2004)Ozger, S., & Mays, L. W. (2004). Optimal location of isolation valves in water distribution systems: a reliability/optimization approach. In L. W. Mays (Ed.), Water resource systems management tools (chap. 7.1-7.24). New York: McGraw-Hill Education. showed a Simulated Annealing algorithm to solve the WDN segmentation problem, where the objective function can be either the reliability or the availability of the given network. Authors such as Cattafi et al. (2011)Cattafi, M., Gavanelli, M., Nonato, M., Alvisi, S., & Franchini, M. (2011). Optimal placement of valves in a water distribution network with CLP(FD). Theory and Practice of Logic Programming, 11(4-5), 731-747. http://dx.doi.org/10.1017/S1471068411000275.
http://dx.doi.org/10.1017/S1471068411000...
, Creaco et al. (2010)Creaco, E., Franchini, M., & Alvisi, S. (2010). Optimal placement of isolation valves in water distribution systems based on valve cost and weighted average demand shortfall. Water Resources Management, 24(15), 4317-4338. http://dx.doi.org/10.1007/s11269-010-9661-5.
http://dx.doi.org/10.1007/s11269-010-966...
and Giustolisi & Savic (2010)Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530.
http://dx.doi.org/10.1080/15730620903287...
studied the consequences of the lack of water, during a supply interruption in a WDN to determine the optimal location of isolation valves. Giustolisi & Savic (2010)Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530.
http://dx.doi.org/10.1080/15730620903287...
used a Genetic Algorithm to optimize the multi-objective. They proposed two objective functions that are: the minimization of the number of valves and the minimization of the maximum total undeliverable demand. The authors’ goal is to minimize the costs associated with the deployment of the valve and simultaneously ensure system reliability. In turn, Creaco et al. (2010)Creaco, E., Franchini, M., & Alvisi, S. (2010). Optimal placement of isolation valves in water distribution systems based on valve cost and weighted average demand shortfall. Water Resources Management, 24(15), 4317-4338. http://dx.doi.org/10.1007/s11269-010-9661-5.
http://dx.doi.org/10.1007/s11269-010-966...
presented a similar model. However, instead of minimizing the number of valves allocated, they seek to minimize the total cost of the valves; they relate this cost to the diameter of the valves implanted. However, heuristic algorithms do not guarantee finding the true Pareto front. Therefore, Cattafi et al. (2011)Cattafi, M., Gavanelli, M., Nonato, M., Alvisi, S., & Franchini, M. (2011). Optimal placement of valves in a water distribution network with CLP(FD). Theory and Practice of Logic Programming, 11(4-5), 731-747. http://dx.doi.org/10.1017/S1471068411000275.
http://dx.doi.org/10.1017/S1471068411000...
solved the same problem as Giustolisi & Savic (2010)Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530.
http://dx.doi.org/10.1080/15730620903287...
using Constraint Logic Programming algorithm and found better solutions.
To sum up, there are algorithms that can solve the problem of optimal allocation of valves in a WDN. However, they are usually made based on “simple rules of thumb” using only hydraulic analysis. However, it is important to include the expertise of the decision makers involved as well as the characteristics of the users along the WDN.
Therefore, there is a need to improve the design of the isolation valve system in order to increase network reliability (Giustolisi & Savic, 2010Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530.
http://dx.doi.org/10.1080/15730620903287...
), minimize the costs associated, and, at the same time, minimize the impacts caused by lack of water to consumer units. In this sense, Jun et al. (2007)Jun, H., Loganathan, G. V., Deb, A. K., Grayman, W., & Snyder, J. (2007). Valve distribution and impact analysis in water distribution systems. Journal of Environmental Engineering, 133(8), 790-799. http://dx.doi.org/10.1061/(ASCE)0733-9372(2007)133:8(790).
http://dx.doi.org/10.1061/(ASCE)0733-937...
reported that the total effect of the failures in WDN can be evaluated by the following measures: (1) total number of customers out of service, (2) total length of pipes due to network segment expansion, and (3) total water loss in circulation. In addition to these factors, Fontana & Morais (2015)Fontana, M. E., & Morais, D. C. (2015). Segmentation model for water distribution networks based on the characteristics of consumer units. Production, 25(1), 143-156. http://dx.doi.org/10.1590/S0103-65132013005000071.
http://dx.doi.org/10.1590/S0103-65132013...
noted that there are others factors that can measure the social impact of lack of water during a supply disruption, such as the type of economic sector of the consumer unit. According to these authors, the lack of water to two or three residences may not have the same impact as the lack of water in a hospital, even if the amount of water consumed is equivalent. Thus, they proposed a model that combines the characteristics of consumer units, by means of a multi-criteria approach, in an index that can measure the impact of the lack of water in the network segments. Thus, the investment with the valves is performed not only on technical issues, but also on the real social needs in the WDN under consideration.
However, this model did not take into account the technical aspects of the difficulties in the implementation of the alternatives. Moreover, it considered only one decision maker. However, water supply issues involve society as a whole and, therefore, they involve multiple decision makers (Morais et al., 2013Morais, D. C., Almeida, A. T., & Figueira, J. R. (2013). A sorting model for group decision making: a case study of water losses in Brazil. Group Decision and Negotiation, 23(5), 937-960. http://dx.doi.org/10.1007/s10726-012-9321-7.
http://dx.doi.org/10.1007/s10726-012-932...
). In these cases the complexity of decision-making is enlarged. According to Fontana & Morais (2016)Fontana, M. E., & Morais, D. C. (2016). Decision model to control water losses in distribution networks. Production, 26(4), 688-697. http://dx.doi.org/10.1590/0103-6513.201815.
http://dx.doi.org/10.1590/0103-6513.2018...
the “decision makers are prone to commit errors when the problem under analysis becomes more complex”. Therefore, this increases the need for a study of group decision methods to aid in this process.
Group decision making can play a vital role in situations where multiple actors are involved, each having their own private perceptions of the context and the decision making problem to be tackled (Morais & Almeida, 2010Morais, D., & Almeida, A. (2010). Water network rehabilitation: a group decision-making approach. Water S.A., 36(4), 487-493. http://dx.doi.org/10.4314/wsa.v36i4.58425.
http://dx.doi.org/10.4314/wsa.v36i4.5842...
). Difficulties related to the group decision-making process in the water supply sector, such as physical and economic losses, irrational use of water, and maintenance costs, highlight the need to develop procedures to support decisions, reducing unnecessary water use and wastage (Trojan & Morais, 2012bTrojan, F., & Morais, D. C. (2012b). Prioritizing alternatives for maintenance of water distribution networks: a group decision approach. Water S.A., 38(4), 555-514. http://dx.doi.org/10.4314/wsa.v38i4.11.
http://dx.doi.org/10.4314/wsa.v38i4.11...
). In the literature, we found some works that use multi-criteria group decision-making methods to solve different maintenance problems in WDN, such as Morais & Almeida (2010)Morais, D., & Almeida, A. (2010). Water network rehabilitation: a group decision-making approach. Water S.A., 36(4), 487-493. http://dx.doi.org/10.4314/wsa.v36i4.58425.
http://dx.doi.org/10.4314/wsa.v36i4.5842...
, Morais et al. (2010)Morais, D. C., Cavalcante, C. A. V., & Almeida, A. T. (2010). Prioritization of areas of loss control in water distribution networks. Pesquisa Operacional, 30(1), 15-32. http://dx.doi.org/10.1590/S0101-74382010000100002.
http://dx.doi.org/10.1590/S0101-74382010...
, Trojan & Morais (2012aTrojan, F., & Morais, D. C. (2012a). Using Electre TRI to support maintenance of water distribution networks. Pesquisa Operacional, 32(2), 423-442. http://dx.doi.org/10.1590/S0101-74382012005000013.
http://dx.doi.org/10.1590/S0101-74382012...
, bTrojan, F., & Morais, D. C. (2012b). Prioritizing alternatives for maintenance of water distribution networks: a group decision approach. Water S.A., 38(4), 555-514. http://dx.doi.org/10.4314/wsa.v38i4.11.
http://dx.doi.org/10.4314/wsa.v38i4.11...
).
In the WDN segmentation problem, Silva Filho et al. (2014)Silva Filho, J. L., Fontana, M. E., & Morais, D. C. (2014, October). Strategic Options Development and Analysis to identify criteria to evaluate segmentation problems of a water distribution network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego. http://dx.doi.org/10.1109/SMC.2014.6973921.
http://dx.doi.org/10.1109/SMC.2014.69739...
proposed a Problem Structuring Method to survey the evaluation criteria of this type of problem. In this sense, they considered a scenario where decision makers come into consensus on the relative importance of the criteria and the evaluation of these alternatives. However, in these types of problems, the decision makers involved may be very divergent, because each one can be from different sectors of water companies, such as the operational, environmental and financial. Thus, an ideal alternative to a DM, in a given time interval, it cannot be an attractive option to another.
Therefore, since previously reported algorithm can result in a different optimal alternative, this paper presents a group decision-making model to assess which of these alternatives is the most appropriate taking into account the technical aspect of the WDN, such as hydraulic issues, and the preferences of the decision makers. We hope that this model will be able to yield an alternative that presents the best compromise regarding the isolation valve allocation in order to maximize the benefits, minimize costs, analyze consumers’ characteristics, and meet the preferences of the decision makers (DMs). For this model, we propose the use of the PROMETHEE Group Decision Support System (GDSS) method. The PROMETHEE GDSS method is used to examine the preferences of group decision-makers and it ranks the alternatives in a descending order of preference according to the value of the net dominance flow associated with each alternative and each decision-maker.
Besides this introduction, this paper is organized as follows: Section 2 presents some considerations about the method used. Section 3 shows the group decision-making model proposed to evaluate the alternatives to WDN segmentation. An application of proposed model and discussions of the results are made in Section 4. Finally, in Section 5 presents some concluding remarks.
2 Materials and methods
There are several methods developed to aid a group of decision-makers. The methods should be chosen according to the rationality of the decision makers. For the proposed model, some aspects need be raised to determine which method is suitable for the case analyzed. This paper assumes that the decision-makers do not want perform trade-off, i.e., they prefer alternatives more balanced. In other words, a “negative” performance of an alternative on a criterion should not be compensated by a “positive” performance on another criterion.
For example, let us consider an alternative with the highest payoff features on the generation of network segments, but, on the other hand, it is that with the largest cost. These are the extreme point in the decision making. In social decisions, the basic principle is to seek by an alternative with lower index of dissatisfaction. Therefore, the maximum benefit must not compensate the highest cost. In this case, an alternative with intermediates benefit and cost will be a better alternative as it will not sacrifice one criterion (cost) for another (benefit). The outranking methods perform a paired comparison of the alternatives and, thus, they are able to evaluate the alternatives for each criterion without making such compensation.
In that perspective, this paper proposes the use of the PROMETHEE method, which consists in a multi-criteria outranking method wherein a set of alternatives will be selected or ranked through the criteria often-conflicting (Brans et al., 1986Brans, J. P., Vincke, P., & Mareschal, B. (1986). How to select and how to rank projects: the PROMETHEE method for MCDM. European Journal of Operational Research, 24(2), 228-238. http://dx.doi.org/10.1016/0377-2217(86)90044-5.
http://dx.doi.org/10.1016/0377-2217(86)9...
). This method adequately fits the problem since examines the preferences of decision-makers and ranks the alternatives according to their compromise with the criteria evaluated. Therefore, PROMETHEE GDSS (Group Decision Support System) method is appropriate for this problem since it allows an analysis of individual opinions and, then, aggregates it to have a collective solution. It allows decision makers to visualize the differences between their preferences to the whole group. Thus, Brans & Vincke (1985)Brans, J. P., & Vincke, P. H. (1985). A preference ranking organization method: the PROMETHEE method. Management Science, 31, 647-656. http://dx.doi.org/10.1287/mnsc.31.6.647.
http://dx.doi.org/10.1287/mnsc.31.6.647...
reported that the procedure of PROMETHEE GDSS consists of three stages, described by Brans & Mareschal (2009)Brans, J. P., & Mareschal, B. (2009). PROMETHEE methods. In J. R. Figueira, S. Greco & M. Ehrgott (Eds.), Multiple criteria decision analysis: state of the art surveys (pp. 163-195). New York: Springer-Verlag. Retrieved in 23 November 2013, from http://www.springer.com/it/book/9780387230672
http://www.springer.com/it/book/97803872...
and Macharis et al. (1998)Macharis, C., Brans, J. P., & Mareschal, B. (1998). The GDSS PROMETHEE procedure – a PROMETHEE-GAIA based procedure for group decision support. Journal of Decision Systems, 7, 283-307.: preliminary, individual evaluation, and global evaluation.
The preliminary stage is useful for generating alternatives and criteria, namely, it will structure the decision problem in a multi-criteria format. The individual evaluation stage allows the decision maker to express his/her preferences and evaluates the result using the PROMETHEE method. The global stage of assessment seeks consensus and minimizes conflicts among decision makers.
3 Group multi-criteria decision making approach for water distribution network segmentation
The proposed model is based in the three phases from PROMETHEE GDSS, but it is adapted to the problem of this study. Figure 1 summarizes the steps of this model.
3.1 STEP 1: Initial group interaction
The facilitator meets the decision makers (DMs) together or individually in order to enrich his knowledge of problem. In Brazil, there are maintenance companies with wide knowledge about WDN segmentation. Some water companies are outsourcing this type of activity. Thus, the ideal strategy is that the facilitator is a consultant from this maintenance company, i.e., a person who has knowledge about the problem of allocation of isolation valves. Thus, he can contribute substantially at all stages proposed here. When this external agent is not possible, a Supra decision maker should be chosen, i.e., a member of the team who has more experience and knowledge about the problem and, in conflict cases, he may have greater weight in the final decision.
Thus, the facilitator describes the tasks to the DMs and introduces the problem. It is important to notice that normally, all DMs in the analysis of the WDN segmentation are from the same Water Company. The existence of an analyst is interesting, but the interaction between DMs already exists to a high degree. This allows waiving some formalities.
3.2 STEP 2: Stable set of evaluation criteria
Alternatives are usually generated by computer programs, which offer an optimal or quasi-optimal alternative. However, in most algorithms used, the evaluation is based on the cost of the valve, and/or hydraulic issue, and/or unmet demands by water. But, does this alternative meet the needs of consumers? Is the water network’s performance more important than the costs involved or not? Nevertheless, several questions lead us to realize the need to consider other aspects as well as to consider the opinions of the DMs involved. Therefore, it is important to consider other criteria that will be used to assess which of these alternatives is the most appropriate.
Therefore, during the meeting, the decision makers will define a stable set of k evaluation criteria (g1(.), g2(.),…, gj(.),…, gk(.)). We suggest two steps for this, namely: (1) each decision maker separately, or with the help of the facilitator, surveys the criteria that he/she considers important; (2) all criteria surveyed are then taken to a collective DMs meeting where they discuss which of these criteria will be accepted or discarded. All DMs need to agree on the elimination of a given criterion. If at least one decision maker disagrees it is not eliminated, and the others DMs can assign “0” weight to that criterion. The criteria selected in that process will make it possible to compare the evaluations of the resulting alternative to the different available algorithms, for instance.
3.3 STEP 3: Generation and stable set of alternatives
The alternatives represent a set of isolation valves and their location in the WDN. In this proposal, a representative of the technical team will be responsible for the generation of alternatives, making use or not an optimization software, and it is up to decision makers to accept, change, or remove them. Thus, for that, it should first conduct a survey of some required data (Data collection from WDN).
Based on the criteria identified in the previous step, it observes that decision-makers and/or technical team should evaluate alternatives. Nevertheless, the number of potential alternatives can be approximately 22n, since n is the number of pipes. For this reason, in this case, we suggest that all dominated alternatives should be eliminated before be evaluated by decision makers. Thus, we can include a step of comparison between the alternatives where all those dominated must be eliminated. This comparison will occur in one or more criteria considered technical, i.e., in that the alternatives are easily evaluated by the use of software, for example, and there is no inherent subjectivity that requires evaluation by decision makers.
This process eliminates a considerate number of alternatives and it makes the evaluate process easier. Thus, the facilitator presents the non-dominated alternatives in a meeting with all the DMs and, afterwards, they begin a stage of discussions. From this, an open discussion takes place, alternatives can be canceled, new ones can be proposed or combined ones can be merged, until a stable set of s alternatives (a1, a2, a3, …, as) is reached. This brainstorming procedure is extremely useful, because it often generates alternatives that were eliminated at the beginning. It is important observed that if at least one decision maker disagrees with the elimination of an alternative, the others can evaluate this alternative as “0” (worst evaluation).
3.4 STEP 4: Individual evaluation tables
In this step, where s is the number of alternatives defined in step 3, and k is the number of criteria defined in step 2, the evaluation table (s x k) has to be completed by each decision maker. Some values are introduced in advance by the facilitator if there is an objective agreement on them (prices, volumes, budgets,…). If not, each DM is allowed to introduce his own values. All the DMs implement the same (s x k) matrix.
3.5 STEP 5: Additional PROMETHEE information
Each decision maker develops his own PROMETHEE analysis. The methods from PROMETHEE family assume that DMs are able to evaluate the criteria and weigh them consistently. Thus, the DM gives to each criterion j, such that j = {1, 2, …, k}, a weight wj according to his preferences, such as in Equation 1.
After that, it is necessary to define a preference function P(d) for each criterion j, which describes the preference intensity for an alternative a over another alternative b. This preference is expressed by a number in the interval [0, 1], where 0 indicates no preference or indifference and 1 for strict preference. It represents the behavior or attitude of the decision maker across the differences from pairwise comparison between alternatives in a given criterion {gj (a) - gj (b)} (Brans et al., 1986Brans, J. P., Vincke, P., & Mareschal, B. (1986). How to select and how to rank projects: the PROMETHEE method for MCDM. European Journal of Operational Research, 24(2), 228-238. http://dx.doi.org/10.1016/0377-2217(86)90044-5.
http://dx.doi.org/10.1016/0377-2217(86)9...
; Macharis et al., 2004Macharis, C., Springael, J., Brucker, K., & Verbeke, A. (2004). PROMETHEE and AHP: the design of operational synergies in multicriteria analysis: Strengthening PROMETHEE with ideas of AHP. European Journal of Operational Research, 153(2), 307-317. http://dx.doi.org/10.1016/S0377-2217(03)00153-X.
http://dx.doi.org/10.1016/S0377-2217(03)...
). Six basic types of preference function are possible, that are: Usual criterion, U-shape Criterion, V-shape criterion, Level Criterion, V-shape with Indifference Criterion, and Gaussian Criterion (for more information see: Brans & Mareschal, 2009Brans, J. P., & Mareschal, B. (2009). PROMETHEE methods. In J. R. Figueira, S. Greco & M. Ehrgott (Eds.), Multiple criteria decision analysis: state of the art surveys (pp. 163-195). New York: Springer-Verlag. Retrieved in 23 November 2013, from http://www.springer.com/it/book/9780387230672
http://www.springer.com/it/book/97803872...
).
3.6 STEP 6: Individual PROMETHEE analysis
After applying the method, a ranking of the alternatives is obtained for each decision maker. This can be obtained by “Visual PROMETHEE software”. This software was developed under the supervision and backed by the authors Brans & Mareschal (2009)Brans, J. P., & Mareschal, B. (2009). PROMETHEE methods. In J. R. Figueira, S. Greco & M. Ehrgott (Eds.), Multiple criteria decision analysis: state of the art surveys (pp. 163-195). New York: Springer-Verlag. Retrieved in 23 November 2013, from http://www.springer.com/it/book/9780387230672
http://www.springer.com/it/book/97803872...
.
3.7 STEP 7: Display of the individual investigations
The rankings of each DM are collected and displayed by the facilitator so that the group of all DMs is informed of the potential conflicts.
3.8 STEP 8: Global evaluation
Given R decision makers, the net flow vectors {ϕr (.), r=1, 2, …, R} of all the DMs are collected by the facilitator and put in a (n x R) matrix. Now, each criterion of this matrix expresses the point of view of a particular DM. Here, it is required the similar information that appears in step 5. According to Macharis et al. (1998)Macharis, C., Brans, J. P., & Mareschal, B. (1998). The GDSS PROMETHEE procedure – a PROMETHEE-GAIA based procedure for group decision support. Journal of Decision Systems, 7, 283-307. if a consensus is not reached, after this final solution, the following feedback could be considered: (a) back to the weighting of the DMs; (b) back to the individual evaluations; (c) back to the set of criteria; (d) back to the set of alternatives; and (e) back to the starting phase and to include an additional stakeholder (“DM”) such as a social negotiator or a government mediator. In the sequence a simulation is presented to demonstrate the applicability of the proposed model.
4 Application of the proposed model
The sequence of steps described in the Section 3 will be followed in order to demonstrate its applicability. In this way, the first step is to define the decision makers. Here, the DMs represent strategic areas of Water Company, such as maintenance department (DM1), finance department (DM2) and the infrastructure department (DM3).
After that, it is important to raise a stable set of evaluation criteria. Therefore, based on Silva Filho et al. (2014)Silva Filho, J. L., Fontana, M. E., & Morais, D. C. (2014, October). Strategic Options Development and Analysis to identify criteria to evaluate segmentation problems of a water distribution network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego. http://dx.doi.org/10.1109/SMC.2014.6973921.
http://dx.doi.org/10.1109/SMC.2014.69739...
, seven criteria were surveyed in this paper, which are:
-
•
Cr1 - Cost of the deployment of the isolation valves: the cost is directly proportional to the number of allocated valves and pipe diameter, where they will be allocated. For simplification purposes, we assumed that the valves can only be allocated on secondary pipes, as suggested by NBR 12218/94, and all secondary pipes are of the same diameter. Thus, we take into consideration here the number of valves (in units) because the higher the number of valves, the higher the cost of implementation. Thus, for this individual criterion the water company wants minimization.
-
•
Cr2 - Number of segments generated: we can determine the number of segments generated observed the location of isolation valves given by each alternative (in units). Thus, the higher the number of segments generated, the larger the benefits to society tend to be. Therefore, for this particular criterion, the water company wants maximization.
-
•
Cr3 - Water consumed: regions with high water consumption tend to suffer water shortages more quickly during a supply interruption. Thus, the water company searches for alternatives that allocate a greater number of valves in these regions. Since the water consumed from each pipe is xi, where i={1, 2,..., n}, we can measure the total water consumed in a segment Mj, where j={1, 2, ...., m}, as in Equation 2.
Thus, in order to verify the efficiency of WDN segmentation, we evaluate the variance of water consumption between segments generated, according to Equation 3. This calculation must be done for each feasible solution. In this criterion, the water company wants minimization.
Where:
-
•
Cr4 – Difficulty level in implementing and maintaining the isolation valves: this is a subjective criterion and a technical team will evaluate it. The team needs to measure the level of the difficulty in implementing the isolation valves suggested by each alternative as well as the difficulties that will be involved when performing future maintenance. First, the technical team can establish an evaluation scale. In this paper, we suggest the scale shown in Table 1. Based on this scale, for this particular criterion, the water company wants maximization.
-
•
Cr5 – Change in network pressure and/or water flow: DMs will evaluate whether the locations of the valves will result in changes in the network’s pressure and/or water flow, which in turn creates the need for additional devices, such as pressure reducing valves. This type of need leads to an implementation cost increase and hinders the execution of the alternative. The technical team can also establish the evaluation scale for this criterion. In this study, we suggest the scale shown in Table 2. Based on this scale, for this particular criterion, the water company wants maximization.
-
•
Cr6 - Type of economies: This criterion checks whether the alternative prioritizes some specific types of consumers, such as hospitals. It is important that this type of consumer be minimally impacted by lack of water during maintenance periods. Therefore, more isolation valves are necessary around these consumers. In order to analyze this criterion, DMs should first classify the types of consumers by areas or economic sectors. In this study, we suggest the classification shown in Table 3. In this table, the classes are ordered from high-priority to less high-priority consumers. After that, they will observe the types of customers located in the district-metered areas (DMA) analyzed and, then, they will evaluate if the alternative allocation of valves is suitable to the needs of that class. For example: Let us consider that there is a hospital in the DMA analyzed. This type of consumer unit has a high need for valves placed close to it; so, that it is possible to minimize water stoppages events during maintenance activities. After that, the DMs will check the degree of suitability of the alternative for the requirements of that class, as a similar scale presented in Table 4. This degree of suitability is somewhat subjective and DMs have different points of view. Consequently, each one of the DMs will individually evaluate the alternatives in this criterion. Based on the scale shown in Table 4, for this individual criterion, the water company wants maximization.
-
•
Cr7 – Infrastructure impact: This criterion measures possible infrastructure problems in the region due to the required conditions for water network’s adequacy. Since DMs are from different areas, we suggest an individual evaluation be done here, where each decision-maker will assess the impacts of each alternative based on their responsibilities. Hence, the scale shown in the Table 5 can express the level of impact generated by each alternative. Based on this scale, for this particular criterion, the water company wants maximization.
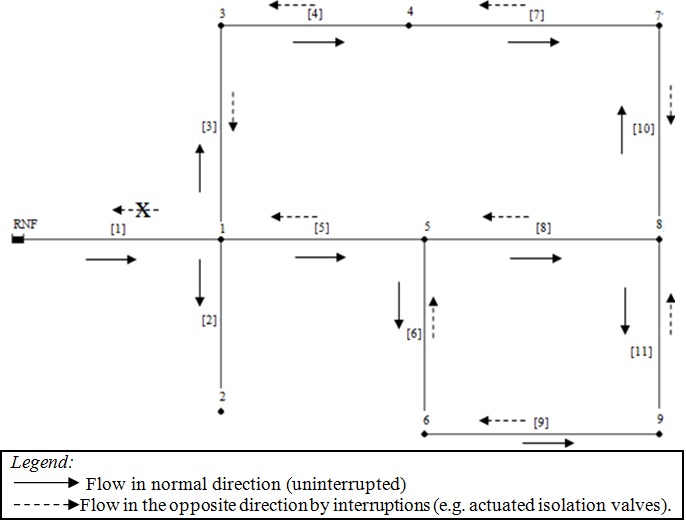
Note that, the values in the criteria Cr3, Cr5 and Cr6 can change as new connections are made in the network. Because of that fact, WDN segmentation problems are dynamic. Consequently, they are usually revised. Thus, an applicable method in existing networks is advised as has been proposed here. Moreover, other criteria are possible, depending on the characteristics of each WDN and the preferences of decision makers. In sequence, after the survey of criteria, it is need to survey the set of alternatives. Thus, a smaller district metered areas (DMA), shown in Figure 2, is used to simulate this. In real cases are common to use DMA to solve WDN segmentation problems.
In Figure 2, the pipe [1] is primary, i.e., it supplies the other pipes that are secondary. Note that in meshed networks when there is an interruption in the normal water flow, water can overcome these obstacles. To improve understanding, let us imagine a single isolation valve next to the node 1 in the pipe [3] (address = [3]/1). In this case, the water flow does not come directly out of the pipe [1] to [3], but will make a turn, through pipe [4] before reaching pipe [3].
It is clear that, in these cases, shutdown of isolation valves generates abnormal working conditions because of the induced topological modification of the network, which may reduce the hydraulic capacity of the water system with respect to the portions still connected (Giustolisi et al., 2014Giustolisi, O., Berardi, L., & Laucelli, D. (2014). Optimal water distribution network design accounting for valve shutdowns. Journal of Water Resources Planning and Management, 140(3), 277-287. http://dx.doi.org/10.1061/(ASCE)WR.1943-5452.0000327.
http://dx.doi.org/10.1061/(ASCE)WR.1943-...
). However, the most important point is to note that the allocation of just this valve [3]/1 would not prevent water flow to any pipe in the WDN. Due to this fact, among others, not all possible allocations valves are admissible.
Therefore, the ideal strategy is to use some method to generate these alternatives. It is important to highlight the procedure described here can be applied to any set of alternatives, without necessarily considering a specific method in their generation. In Brazil, for example, is common generates the alternatives through network analysis by EPANET software. In this work, the alternatives were generated through deterministic method based on combinatory step, where it is ranging the number of valves and their location in the network. Moreover, in this simulation, in compliance with NBR 12218/94 (Associação Brasileira de Normas Técnicas, 1994Associação Brasileira de Normas Técnicas. (1994). NBR 12218/1994: project of water distribution network for public supply. Rio de Janeiro: ABNT. Retrieved in 5 April 2012, from http://www.abnt.org.br/
http://www.abnt.org.br/...
), all the alternatives will contain at least 03 valves located in [2]/1, [5]/1 and [3]/1, i.e., valves placed in the secondary pipes near the point of attachment to the main pipes. When the analysis is done on an existing network, all existing valves should be considered in the solutions. However, due to the high number of possibilities in real cases, heuristics methods are more appropriate.
In sequence, only the non-dominated alternatives will be considered. Any criterion can be considered in this dominated relationship. However, we consider the performance of the alternatives in three criteria, which are: Cr1, Cr2 and Cr3. This is because the evaluation of the alternatives on these criteria is made by computation program. Therefore, only the non-dominated alternatives will be evaluate on other criteria by decision makers.
Therefore, the evaluation of alternatives on the criteria Cr1 to Cr5 is the same for all decision makers. In the criteria Cr6 and Cr7, the evaluation of alternatives depends of the each decision maker. For example, the location of a valve in a pipe located in a path with large movement of vehicles should be deprecated when it is compared to a path with less movement (criterion Cr7). However, not all DMs have the same perception over this point. Therefore, the DMs will evaluate the alternatives by means of a set of intrinsic aspects of their experience, i.e., each DM will evaluate the alternatives according to their responsibility in the company. Table 6 presents the subset of established alternatives as well as the individual evaluation from the three decision makers.
The weights, preference function and thresholds given by each decision maker can be seen in Table 7. Note that the facilitator, especially in cases where the DMs do not have much familiarity with the PROMETHEE method, should support this process.
Table 8 shows the individual PROMETHEE II rankings. Finally, these ranks form the new matrix. Thus, it is interesting to use the same preference function for all DMs. In this case is the Usual. Moreover, as all decision makers occupy the same place in the hierarchy of the supply company, although in different sectors, all of them have the same weight in the final decision. When the decision making involves external decision makers, such as government representatives, it should consider the need to assign different weights for their opinions. Table 8 shows the global PROMETHEE II ranking.
4.1 Sensitivity analysis
Observing the results, in Table 8, we can see that DM2 shows the greatest divergence in relation to the result. This demonstrates the importance of well-defined weights, when in scenarios of divergence between the decision makers. For that, we performed a sensitivity analysis to verify the robustness of the model. Here, we simulate the existence of DMs with greater weight in the final decision, such as a Supra decision maker. For this, we oscillate the weight of each decision maker in ± 10%, redistributing the difference in the sum of the weight to the other DMs equally. In all cases there were no changes in the chosen alternative (A6), reinforcing the adoption of this.
Continuing the sensitivity analysis, we simulated the consequences when the weight of each criterion oscillated in ±5%, increasing or decreasing the weight of the other criteria proportionally, such that the sum of the weights of the criteria must be equal to 1 (see Equation 1). In addition, for each change of the weights of the criteria were simulated three new situations: (1) decision makers with equal weight (standard situation); (2) each decision maker with -10% of his weight; (3) each decision maker with +10% of his weight. In cases (2) and (3) the difference in the sum of the weights is redistributed to other DMs equally. Thus, for each oscillation of a weight of the criterion seven cases are simulated, i.e., ninety-eight cases in total. Only in the case of oscillation of + 5% in the weight of criterion Cr3 occurs change in the ranking, when the winning alternative is A9 and A6 is the second placed. However, in this case, when it changed the weight of decision makers at -10% for DM1 and DM3 these alternatives appear tied. The best performance of the alternative A9 in this criterion made the difference when the criterion received greater weight.
4.2 Discussion of the results
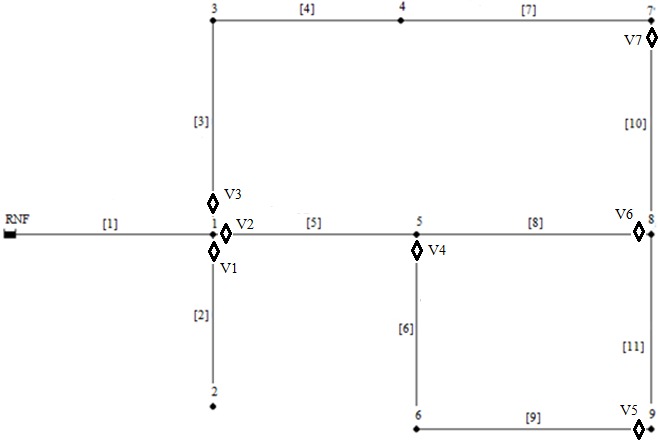
The results showed that the PROMETHEE GDSS method is able to minimize conflicts between decision makers. This is because, although there are divergences in the opinions from DMs, this method result in an intermediate alternative, since the winning alternative (A6) is among the best in every individual ranks. Figure 3 shows the location of the valves in the chosen alternative (A6 = [2]/1, [3]/1, [5]/1, [6]/5, [8]/8, [9]/9 and [10]/7), with 07 valves (Vi) and 05 network segments are formed.
It is important to note that if we used the N-1 rule (A12), the WDN would have 12 isolation valves. This will be more significant the larger the network under consideration. The alternative A12 is an “extreme” alternative, i.e., it presents the greatest benefits (Cr2, Cr3 and Cr6), but also the worst performances (Cr1, Cr4 and Cr7). While the alternative A6 shows a balanced performance in all criteria. Thus, it is possible to find an alternative with lower index of dissatisfaction among decision makers.
Another important point is that the best alternative (A6) does not appear in last place in individuals’ ranks for all scenarios simulated in the sensitivity analysis. Thus, the proposed model prevents the adoption of the worst alternatives for a decision maker. Therefore, this result shows that the proposal methodology is robust and achieve its objective, that is choice an equilibrate alternative to all decision makers.
In real cases, the result, after the sensitivity analysis, may not converge to only one alternative. However, with the help of this proposed model, it is possible to reach a subset of the best alternatives and, then, it can take a step with discussion based only on these alternatives, facilitating the individual analyses. We can even reapply the proposed method.
5 Concluding remarks
As discussed before, decisions about WDN segmentation involve society as a whole, since it suffers the impact of the lack of water during the maintenance activities. Thus, it is important that the Water Company make decisions that are technically and economically viable while benefiting consumers. Moreover, this decision can involve more than one decision maker. Therefore, we believe that the main contribution of this work was to propose a model that is able to aid the decision makers in group decision-making procedure to WDN segmentation, and at same time consider factors that are relevant to the consumers. Its relevance is further enhanced by the complex decision-making environment. The proposed model used the PROMETHEE GDSS method to support the phases of the decision-making on which alternative of network segmentation adopt.
One of the advantages of applying this model is that it ensures that the worst alternative in the all opinion does not appear in the top positions in the global rank. This minimizes the adoption of alternatives that can raise the level of dissatisfaction and disagreement between decision makers. Additionally allows further reduce the set of alternatives, facilitating discussions among DMs.
Moreover, the proposal method allows to work with subjective criteria and not just with technical data. After all, on issues that affect society, like this, taking purely technical decisions (hydraulic, for example) may not represent the actual needs. Thus, we must consider other factors, as demonstrated in this work.
Importantly, in existing WDNs, the analysis over allocation valves is commonly made into district metered areas (DMA), i.e., in small portions of the network, which reinforces the applicability of this proposed model without increase in complexity.
One limitation of this model is the need of an analyst, especially when there is no leveling of knowledge about the application of the method among DMs. In conflicting environments, such as the case presented, the analyst emerges as an interesting intermediary figure.
Although in practice most water supply companies do not take these decisions with multiple decision-makers from different departments, this work emphasizes the importance of doing this. It is because this decision affects other departments and they can evaluate the problem watching others relevant issues such as those raised in this paper. In this way, as future work, we recommend an application of the proposed model in a real case, although the simulation has already shown satisfactory results, it is necessary to discuss the real difficult from decision makers in establishing the required parameters.
-
How to cite this article: Fontana, M. E., & Morais, D. C. (2017). Water distribution network segmentation based on group multi-criteria decision approach. Production, v. 27, e20162083. http://dx.doi.org/10.1590/0103-6513.208316
References
- Associação Brasileira de Normas Técnicas. (1994). NBR 12218/1994: project of water distribution network for public supply. Rio de Janeiro: ABNT. Retrieved in 5 April 2012, from http://www.abnt.org.br/
» http://www.abnt.org.br/ - Brans, J. P., & Mareschal, B. (2009). PROMETHEE methods. In J. R. Figueira, S. Greco & M. Ehrgott (Eds.), Multiple criteria decision analysis: state of the art surveys (pp. 163-195). New York: Springer-Verlag. Retrieved in 23 November 2013, from http://www.springer.com/it/book/9780387230672
» http://www.springer.com/it/book/9780387230672 - Brans, J. P., & Vincke, P. H. (1985). A preference ranking organization method: the PROMETHEE method. Management Science, 31, 647-656. http://dx.doi.org/10.1287/mnsc.31.6.647
» http://dx.doi.org/10.1287/mnsc.31.6.647 - Brans, J. P., Vincke, P., & Mareschal, B. (1986). How to select and how to rank projects: the PROMETHEE method for MCDM. European Journal of Operational Research, 24(2), 228-238. http://dx.doi.org/10.1016/0377-2217(86)90044-5
» http://dx.doi.org/10.1016/0377-2217(86)90044-5 - Cattafi, M., Gavanelli, M., Nonato, M., Alvisi, S., & Franchini, M. (2011). Optimal placement of valves in a water distribution network with CLP(FD). Theory and Practice of Logic Programming, 11(4-5), 731-747. http://dx.doi.org/10.1017/S1471068411000275
» http://dx.doi.org/10.1017/S1471068411000275 - Creaco, E., Franchini, M., & Alvisi, S. (2010). Optimal placement of isolation valves in water distribution systems based on valve cost and weighted average demand shortfall. Water Resources Management, 24(15), 4317-4338. http://dx.doi.org/10.1007/s11269-010-9661-5
» http://dx.doi.org/10.1007/s11269-010-9661-5 - Di Nardo, A., Di Natale, M., Santonastaso, G. F., Tzatchkov, V. G., & Alcocer-Yamanaka, V. H. (2014). Water network sectorization based on genetic algorithm and minimum dissipated power paths. Water Science and Technology: Water Supply, 13(4), 951-957. http://dx.doi.org/10.2166/ws.2013.059
» http://dx.doi.org/10.2166/ws.2013.059 - Fontana, M. E., & Morais, D. C. (2013). Using PROMETHEE V to select alternatives so as to rehabilitate water supply network with detected leaks. Water Resources Management, 27(11), 4021-4037. http://dx.doi.org/10.1007/s11269-013-0393-1
» http://dx.doi.org/10.1007/s11269-013-0393-1 - Fontana, M. E., & Morais, D. C. (2015). Segmentation model for water distribution networks based on the characteristics of consumer units. Production, 25(1), 143-156. http://dx.doi.org/10.1590/S0103-65132013005000071
» http://dx.doi.org/10.1590/S0103-65132013005000071 - Fontana, M. E., & Morais, D. C. (2016). Decision model to control water losses in distribution networks. Production, 26(4), 688-697. http://dx.doi.org/10.1590/0103-6513.201815
» http://dx.doi.org/10.1590/0103-6513.201815 - Giustolisi, O., & Ridolfi, L. (2014). New modularity-based approach to segmentation of water distribution networks. Journal of Hydraulic Engineering, 140(10), 04014049. http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000916
» http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000916 - Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water Journal, 7(1), 1-15. http://dx.doi.org/10.1080/15730620903287530
» http://dx.doi.org/10.1080/15730620903287530 - Giustolisi, O., Berardi, L., & Laucelli, D. (2014). Optimal water distribution network design accounting for valve shutdowns. Journal of Water Resources Planning and Management, 140(3), 277-287. http://dx.doi.org/10.1061/(ASCE)WR.1943-5452.0000327
» http://dx.doi.org/10.1061/(ASCE)WR.1943-5452.0000327 - Giustolisi, O., Kapelan, Z., & Savic, D. (2008). Extended period simulation analysis considering valve shutdowns. Journal of Water Resources Planning and Management, 134(6), 527-537. http://dx.doi.org/10.1061/(ASCE)0733-9496(2008)134:6(527)
» http://dx.doi.org/10.1061/(ASCE)0733-9496(2008)134:6(527) - Heller, L., & Pádua, V. L. (2006). Water supply for human consumption. Belo Horizonte: UFMG.
- Jun, H., & Loganathan, G. V. (2007). Valve-controlled segments in water distribution systems. Journal of Water Resources Planning and Management, 133(2), 145-155. http://dx.doi.org/10.1061/(ASCE)0733-9496(2007)133:2(145)
» http://dx.doi.org/10.1061/(ASCE)0733-9496(2007)133:2(145) - Jun, H., Loganathan, G. V., Deb, A. K., Grayman, W., & Snyder, J. (2007). Valve distribution and impact analysis in water distribution systems. Journal of Environmental Engineering, 133(8), 790-799. http://dx.doi.org/10.1061/(ASCE)0733-9372(2007)133:8(790)
» http://dx.doi.org/10.1061/(ASCE)0733-9372(2007)133:8(790) - Macharis, C., Brans, J. P., & Mareschal, B. (1998). The GDSS PROMETHEE procedure – a PROMETHEE-GAIA based procedure for group decision support. Journal of Decision Systems, 7, 283-307.
- Macharis, C., Springael, J., Brucker, K., & Verbeke, A. (2004). PROMETHEE and AHP: the design of operational synergies in multicriteria analysis: Strengthening PROMETHEE with ideas of AHP. European Journal of Operational Research, 153(2), 307-317. http://dx.doi.org/10.1016/S0377-2217(03)00153-X
» http://dx.doi.org/10.1016/S0377-2217(03)00153-X - Mays, L. W. (Org.). (2000). Water distribution systems handbook. New York: McGraw-Hill.
- Morais, D. C., Almeida, A. T., & Figueira, J. R. (2013). A sorting model for group decision making: a case study of water losses in Brazil. Group Decision and Negotiation, 23(5), 937-960. http://dx.doi.org/10.1007/s10726-012-9321-7
» http://dx.doi.org/10.1007/s10726-012-9321-7 - Morais, D. C., Cavalcante, C. A. V., & Almeida, A. T. (2010). Prioritization of areas of loss control in water distribution networks. Pesquisa Operacional, 30(1), 15-32. http://dx.doi.org/10.1590/S0101-74382010000100002
» http://dx.doi.org/10.1590/S0101-74382010000100002 - Morais, D., & Almeida, A. (2010). Water network rehabilitation: a group decision-making approach. Water S.A., 36(4), 487-493. http://dx.doi.org/10.4314/wsa.v36i4.58425
» http://dx.doi.org/10.4314/wsa.v36i4.58425 - Ozger, S., & Mays, L. W. (2004). Optimal location of isolation valves in water distribution systems: a reliability/optimization approach. In L. W. Mays (Ed.), Water resource systems management tools (chap. 7.1-7.24). New York: McGraw-Hill Education.
- Silva Filho, J. L., Fontana, M. E., & Morais, D. C. (2014, October). Strategic Options Development and Analysis to identify criteria to evaluate segmentation problems of a water distribution network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego. http://dx.doi.org/10.1109/SMC.2014.6973921
» http://dx.doi.org/10.1109/SMC.2014.6973921 - Trojan, F., & Morais, D. C. (2012a). Using Electre TRI to support maintenance of water distribution networks. Pesquisa Operacional, 32(2), 423-442. http://dx.doi.org/10.1590/S0101-74382012005000013
» http://dx.doi.org/10.1590/S0101-74382012005000013 - Trojan, F., & Morais, D. C. (2012b). Prioritizing alternatives for maintenance of water distribution networks: a group decision approach. Water S.A., 38(4), 555-514. http://dx.doi.org/10.4314/wsa.v38i4.11
» http://dx.doi.org/10.4314/wsa.v38i4.11 - Walski, T. M. (1993a). Practical aspects of providing reliability in water distribution systems. Reliability Engineering & System Safety, 42(1), 13-19. http://dx.doi.org/10.1016/0951-8320(93)90050-9
» http://dx.doi.org/10.1016/0951-8320(93)90050-9 - Walski, T. M. (1993b). Water Distribution Valve Topology for reliability analysis. Reliability Engineering & System Safety, 42(1), 1-21. http://dx.doi.org/10.1016/0951-8320(93)90051-Y
» http://dx.doi.org/10.1016/0951-8320(93)90051-Y
Publication Dates
-
Publication in this collection
2017
History
-
Received
04 Mar 2016 -
Accepted
20 Feb 2017