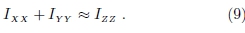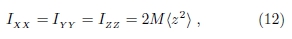Apresentamos a forma geral do teorema dos eixos perpendiculares, a qual pode ser aplicada a qualquer corpo rígido, e obtemos a sua versão válida para qualquer sólido de revolução. Apresentamos, ainda, o seu caso particular para cilindros gerais retos. Alguns exemplos são feitos com o intuito de mostrarmos como pode ser simplificada a determinação de momentos de inércia de certos corpos rígidos se fizermos uso deste teorema.
corpo rígido; teorema dos eixos perpendiculares; sólido de revolução; cilindro geral reto
We present the general form of the perpendicular axis theorem, which can be applied to any rigid body, and we obtain its version valid for any solid of revolution. We also present a particular case for right general cylinders. Some examples are given in order to show how the determination of moments of inertia of certain rigid bodies can be simplified if we use this theorem.
rigid body; perpendicular axis theorem; solid of revolution; right general cylinder
ARTIGOS GERAIS
O teorema dos eixos perpendiculares para um corpo rígido qualquer
The perpendicular axis theorem for any rigid body
Ana Maria Senra Breitschaft1; Valmar Carneiro Barbosa
Instituto de Física, Universidade Federal do Rio de Janeiro, Rio de Janeiro, RJ, Brasil
RESUMO
Apresentamos a forma geral do teorema dos eixos perpendiculares, a qual pode ser aplicada a qualquer corpo rígido, e obtemos a sua versão válida para qualquer sólido de revolução. Apresentamos, ainda, o seu caso particular para cilindros gerais retos. Alguns exemplos são feitos com o intuito de mostrarmos como pode ser simplificada a determinação de momentos de inércia de certos corpos rígidos se fizermos uso deste teorema.
Palavras-chave: corpo rígido, teorema dos eixos perpendiculares, sólido de revolução, cilindro geral reto.
ABSTRACT
We present the general form of the perpendicular axis theorem, which can be applied to any rigid body, and we obtain its version valid for any solid of revolution. We also present a particular case for right general cylinders. Some examples are given in order to show how the determination of moments of inertia of certain rigid bodies can be simplified if we use this theorem.
Keywords: rigid body, perpendicular axis theorem, solid of revolution, right general cylinder.
1. Introdução
Corpo rígido é uma aproximação para um sistema de partí culas cujas distâncias relativas entre seus constituintes podem ser consideradas inalteradas durante os seus movimentos. Como é bem conhecido (veja, por exemplo, Ref. [1]), para descrevermos os possí veis movimentos de um corpo rí gido é necessário conhecermos suas propriedades inerciais: a massa e o tensor de inércia em relação a um referencial. Tais propriedades estão associadas às dificuldades de se alterar, respectivamente, os movimentos do centro de massa do corpo rí gido e de rotação deste corpo em torno de um eixo. Dependendo da forma do corpo rí gido e do referencial escolhido, a determinação do tensor de inércia pode não ser simples. Entretanto, existem alguns teoremas que podem auxiliar em tal determinação, sendo os mais conhecidos (veja, por exemplo, Ref. [1]) o teorema dos eixos paralelos, também conhecido como teorema de Huygens-Steiner, e o teorema dos eixos perpendiculares. O primeiro relaciona o momento de inércia de um corpo rí gido em relação a um eixo que passe pelo seu centro de massa com o seu momento de inércia em relação a qualquer eixo paralelo a esse; o segundo é uma relação entre os elementos da diagonal do tensor de inércia.
Embora o teorema dos eixos paralelos seja abordado por todos os livros sobre mecânica clássica que tratam do assunto relacionado a corpo rí gido e que são comumente adotados em diferentes ní veis do ensino superior [1-8], este não é o caso do teorema dos eixos perpendiculares. Neste caso, em tais livros, ou o assunto não é abordado [7], ou é apresentado, seja como um problema sugerido [2, 4, 5] ou ao longo do texto [1, 3, 6, 8], de uma forma válida apenas para corpos rí gidos laminares, isto é, corpos rí gidos cujos constituintes estão distribuí dos aproximadamente sobre um plano. Por outro lado, há muito tempo atrás, quando estivemos envolvidos em uma disciplina de ní vel intermediário sobre mecânica clássica, demonstramos o teorema dos eixos perpendiculares para qualquer corpo rí gido e, graças à sua simplicidade e à sua surpreendente capacidade em facilitar a determinação de momentos de inércia de corpos rí gidos de interesse, temos, desde então, apresentado esta forma geral do teorema na disciplina de ní vel introdutório sobre mecânica clássica. Recentemente, porém, descobrimos que a forma geral do teorema em discussão não é uma novidade, pois, pelo menos, aparece em uma lista de alguns teoremas relativos a momentos de inércia em um livro publicado na década de 1930 [9]. Na década de 1980, a forma geral deste teorema foi redescoberta por McKelvey [10].
Apesar disto, decidimos escrever o presente artigo por diversos motivos. Primeiramente, na Ref. [9] o autor apresenta alguns teoremas relacionados a momentos de inércia, mas não chama a atenção do leitor para o fato de que um deles é a forma geral do teorema dos eixos perpendiculares e sequer explora as facilidades que a utilização deste teorema pode trazer. Um outro motivo é que no artigo da Ref. [10] o autor, apesar de explorar alguns pontos importantes da aplicação do teorema em discussão, consome uma parte substancial do texto apresentando dois exemplos complicados (um octaedro regular e uma lente plano-convexa), o que, do nosso ponto de vista, compromete a clareza de seu objetivo. Ainda, por acharmos tão interessante, do ponto de vista prático, a generalização deste teorema, concluí mos que não seria demais tirá-lo do aparente esquecimento, o que deve ser facilitado pela versão digital livre do presente meio de publicação. E, finalmente, porque chegamos a uma forma particular deste teorema que o torna ainda mais poderoso na determinação de momentos de inércia de corpos rí gidos de revolução.
Assim sendo, o presente artigo encontra-se organizado da seguinte maneira: na Sec. 2, apresentamos a demonstração do teorema em discussão, que, a partir daqui, denomiraremos apenas como Teorema dos Eixos Perpendiculares; na Sec. 3, apresentaremos algumas consequências imediatas deste teorema; na Sec. 4, apresentaremos os casos particulares deste teorema para sólidos de revolução e para sólidos do tipo cilindro geral reto e, finalmente, na Sec. 5, apresentaremos alguns exemplos com o objetivo de ressaltar os benefí cios da utilização deste teorema.
2. O teorema
Na Fig. 1, encontra-se esquematizado um corpo rí gido genérico de volume V. Um elemento infinitesimal de volume deste corpo rígido (dV) é localizado por um observador em O pelo vetor posição r e contém uma quantidade infinitesimal de massa dada por ρ(r) dV, onde ρ(r) representa a densidade volumétrica de massa deste corpo rí gido na posição r. A massa total deste corpo rí gido (M) é, portanto, dada por
Como haví amos dito logo no iní cio da introdução deste artigo, para descrevermos os possí veis movimentos de um corpo rí gido precisamos conhecer sua massa e sua outra propriedade inercial chamada de tensor de inércia em relação a um sistema de eixos ortogonais entre si, como, por exemplo, os eixos X, Y e Z que aparecem na Fig. 1. Este tensor é um tensor de segunda ordem simétrico, cujas componentes IXiXj (com i e j podendo assumir os valores 1, 2 e 3) podem ser escritas da seguinte forma (veja, por exemplo, Ref. [11])
onde, para escrevermos o menor número possí vel de equações, trocamos temporariamente os nomes dos eixos X, Y e Z por, respectivamente, X1, X2 e X3, r é a magnitude do vetor r, δij é a delta de Kronecker e Xi é a coordenada associada ao eixo Xi. Os três elementos da diagonal deste tensor (j=i), dados por
são conhecidos como os momentos de inércia de um corpo rí gido em relação a cada um dos eixos escolhidos. Os demais seis elementos do tensor de inércia, conhecidos como produtos de inércia de um corpo rí gido em relação a um sistema de eixos, são dados por (veja Eq. (2))
o que, devido ao fato de IXiXj=IXjXi, faz com que o tensor em questão seja simétrico, como já mencionado anteriormente.
Para chegarmos à relação que expressa o teorema que estamos considerando neste artigo, devemos, primeiramente, adicionar IXX≡IX1X1 a IYY≡IX2X2, dados pela Eq. (3), o que resulta em
Após notarmos que 2r2-(x2+y2)=(r2-z2)+2z2 e utilizarmos, novamente, a Eq. (3) para identificarmos IZZ≡IX3X3, obteremos que
onde
é o valor médio de z2 ponderado pela densidade volumétrica de massa do corpo rí gido. A Eq. (6), juntamente com a definição acima, expressa o Teorema dos Eixos Perpendiculares válido para qualquer corpo rí gido [9, 10].
3. Consequências
Partindo do princí pio de que a massa de um corpo rí gido (M) possa ser conhecida, o teorema dos eixos perpendiculares, expresso pela Eq. (6), é uma relação que involve os três elementos da diagonal do tensor de inércia deste corpo rí gido (IXX, IYY e IZZ) e o valor médio de z2 para a sua distribuição de massa  , os quais dependem da sua forma geometrica, de como sua massa está distribuí da em seu volume e de um sistema de eixos escolhidos. Portanto, para que este teorema tenha alguma utilidade, é necessário conhecer três destas quantidades fí sicas para se determinar uma quarta ou evocar aproximações e/ou simetrias do sistema em estudo.
, os quais dependem da sua forma geometrica, de como sua massa está distribuí da em seu volume e de um sistema de eixos escolhidos. Portanto, para que este teorema tenha alguma utilidade, é necessário conhecer três destas quantidades fí sicas para se determinar uma quarta ou evocar aproximações e/ou simetrias do sistema em estudo.
Uma aproximação, que reduz de quatro para três as quantidades relacionadas por este teorema, é aquela usada quando podemos considerar um determinado corpo rí gido como tendo sua distribuição de massa praticamente contida em um plano paralelo ao plano XY e definido por uma coordenada z0. Neste caso, a coordenada z de cada um de seus elementos infinitesimais de volume é aproximadamente z0, o que, devido às Eqs. (7) e (1), nos leva a concluir que  . Portanto, para estes casos, o teorema expresso pela Eq. (6) assume uma forma mais simples
. Portanto, para estes casos, o teorema expresso pela Eq. (6) assume uma forma mais simples
Se o plano que contém, aproximadamente, um corpo rí gido laminar for o plano XY (z0=0), a relação acima é transformada na expressão comumente conhecida como o teorema dos eixos perpendiculares (veja, por exemplo, Ref. [1]), ou seja
Devido à Eq. (7) e à discussão apresentada no parágrafo anterior, podemos concluir que
 0 e, portanto, deduzir da Eq. (6) que
0 e, portanto, deduzir da Eq. (6) que
uma consequência interessante do teorema em discussão, válida para qualquer corpo rí gido e para qualquer escolha de sistema de eixos, já notada, pelo menos, por Landau e Lifshitz [8] e por McKelvey [10].
Em certos casos, podemos reduzir o número de quantidades físicas relacionadas pelo teorema dos eixos perpendiculares utilizando simetrias do sistema considerado. Se para um certo corpo rí gido e um sistema de eixos escolhido pudermos concluir que, digamos, IXX=IYY, a Eq. (6) se reduzirá à
significando que o conhecimento de, por exemplo, IZZ e 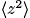 é suficiente para a determinação de todos os elementos da diagonal do tensor de inércia deste sistema. Exemplos de corpos rí gidos que podem se enquadrar nesta situação são aqueles que têm suas massas distribuí das uniformemente pelos seus volumes e formas geométricas com simetria axial, formas de paralelepí pedos ... Há casos em que a simetria do sistema é tal que podemos concluir que IXX=IYY=IZZ e, portanto, podemos escrever a Eq. (6) como
é suficiente para a determinação de todos os elementos da diagonal do tensor de inércia deste sistema. Exemplos de corpos rí gidos que podem se enquadrar nesta situação são aqueles que têm suas massas distribuí das uniformemente pelos seus volumes e formas geométricas com simetria axial, formas de paralelepí pedos ... Há casos em que a simetria do sistema é tal que podemos concluir que IXX=IYY=IZZ e, portanto, podemos escrever a Eq. (6) como
onde vemos que os elementos da diagonal do tensor de inércia de um sistema com tal simetria ficam determinados pelo conhecimento de 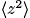 . Como exemplos de sólidos para os quais, dependendo do sistema de eixos escolhido, podemos usar a equação acima, citamos aqueles que, além de serem caracterizados por uma densidade volumétrica de massa uniforme, possuam formas geométricas com simetria esférica, de cubos, de octaedros regulares [10] ...
. Como exemplos de sólidos para os quais, dependendo do sistema de eixos escolhido, podemos usar a equação acima, citamos aqueles que, além de serem caracterizados por uma densidade volumétrica de massa uniforme, possuam formas geométricas com simetria esférica, de cubos, de octaedros regulares [10] ...
4. Determinação de
Nesta seção, determinaremos a quantidade 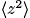 , a qual aparece na Eq. (6) que expressa o teorema dos eixos perpendiculares e é dada pela Eq. (7), para dois tipos de corpos rí gidos: um corpo rí gido de revolução genérico e um cilindro geral reto. Para fazermos isto, suporemos, a partir daqui, que a massa de cada corpo rí gido está distribuí da uniformemente em seu volume, ou seja ρ(r)=ρ0 e ρ0 é uma constante. Com isto, a Eq. (1) pode ser reescrita como M=ρ0V e a Eq. (7) para
, a qual aparece na Eq. (6) que expressa o teorema dos eixos perpendiculares e é dada pela Eq. (7), para dois tipos de corpos rí gidos: um corpo rí gido de revolução genérico e um cilindro geral reto. Para fazermos isto, suporemos, a partir daqui, que a massa de cada corpo rí gido está distribuí da uniformemente em seu volume, ou seja ρ(r)=ρ0 e ρ0 é uma constante. Com isto, a Eq. (1) pode ser reescrita como M=ρ0V e a Eq. (7) para 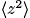 fica bem mais simples
fica bem mais simples
Assim sendo, consideremos o corpo rí gido de revolução genérico esquematizado na Fig. 2. Um corpo rí gido deste tipo é tal que a sua superfí cie é obtida pela rotação de 2π em torno de um eixo, digamos Z, de uma curva descrita por uma função g(z) definida no intervalo [zmin,zmax], conhecida como função geratriz, o que torna este eixo um eixo de simetria axial para tal corpo rí gido. Um sólido deste tipo pode ser considerado como uma pilha de cilindros retos infinitesimais, cada um tendo Z como eixo de simetria axial, raio g(z) e altura dz, como é mostrado na Fig. 2. Portanto, a contribuição infinitesimal de cada um destes cilindros ao volume e ao momento de inércia em relação a Z [12] deste corpo rígido são, respectivamente,
e
Então, para um corpo rí gido de revolução que ocupa o intervalo [zmin,zmax], cuja função geratriz g(z) seja conhecida e, ainda, para o qual ρ0=M/V, as quantidades V, 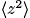 (veja Eq. (13)) e IZZ são dadas, respectivamente, por
(veja Eq. (13)) e IZZ são dadas, respectivamente, por
Como o eixo de simetria axial da distribuição de massa do tipo de corpo rí gido que consideramos até aqui nesta seção foi escolhido por nós como sendo o eixo Z, a Eq. (11) pode ser usada, juntamente com as equações acima, para obtermos todos os elementos da diagonal do tensor de inércia do sistema em questão.
O outro tipo de sólidos que gostarí amos de abordar nesta seção é aquele que é gerado quando uma figura plana de área A é deslocada de uma distância h ao longo de um eixo ortogonal ao plano que a contém e paralelo a, digamos, Z. Um sólido deste tipo pode ser denominado como cilindro geral reto [12] e tem como caso particular um prisma reto quando a sua base de área A é um polí gono. Para um sólido deste tipo, o elemento infinitesimal de volume pode ser escrito como dV=A dz e, por isto, seu volume é dado por V=Ah. Se este sólido estiver entre os planos z=-h/2 e z=h/2, a Eq. (13) nos fornece o seguinte valor para 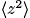
Como veremos na Sec. 5, a utilização da equação acima com a Eq. (11) ou com a Eq. (12) pode facilitar muito a determinação dos elementos da diagonal de corpos rí gidos em forma de cilindros gerais retos. Apesar desta categoria de sólidos já ter sido abordada na Ref. [10], decidimos apresentá-la aqui por acharmos uma categoria importante, da qual fazem parte, por exemplo, o cilindro circular reto e o cubo.
5. Exemplos
Nesta seção, discutiremos alguns exemplos de aplicação do teorema dos eixos perpendiculares. Apesar de termos apresentado, na seção anterior, as relações gerais para as quantidades V, 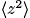 e IZZ para um certo corpo rí gido de revolução em termos da sua função geratriz g(z) (veja Eqs. (16 - 18)), não nos ateremos, aqui, na determinação de V e IZZ (quando necessário), pois podem ser encontrados em vários outros lugares para os sólidos que servirão como exemplos. Daremos ênfase ao cálculo de
e IZZ para um certo corpo rí gido de revolução em termos da sua função geratriz g(z) (veja Eqs. (16 - 18)), não nos ateremos, aqui, na determinação de V e IZZ (quando necessário), pois podem ser encontrados em vários outros lugares para os sólidos que servirão como exemplos. Daremos ênfase ao cálculo de 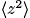 e à exploração de simetrias de um corpo rí gido, mostrando como a aplicação do teorema dos eixos perpendiculares torna a determinação dos demais elementos da diagonal de seu tensor de inércia (IXX e IYY) em uma tarefa simples. Devemos lembrar que tais elementos podem ser calculados diretamente a partir de suas definições (veja Eq. (3)) ou, por exemplo, integrando contribuições de sólidos infinitesimais para os quais conheçamos dIZZ, após, em muitos casos, termos feito uso do teorema dos eixos perpendiculares em sua forma expressa pela Eq. (9) e do teorema dos eixos paralelos. Porém, sempre que possí vel, o uso do teorema dos eixos perpendiculares em sua forma geral facilita muito tais determinações.
e à exploração de simetrias de um corpo rí gido, mostrando como a aplicação do teorema dos eixos perpendiculares torna a determinação dos demais elementos da diagonal de seu tensor de inércia (IXX e IYY) em uma tarefa simples. Devemos lembrar que tais elementos podem ser calculados diretamente a partir de suas definições (veja Eq. (3)) ou, por exemplo, integrando contribuições de sólidos infinitesimais para os quais conheçamos dIZZ, após, em muitos casos, termos feito uso do teorema dos eixos perpendiculares em sua forma expressa pela Eq. (9) e do teorema dos eixos paralelos. Porém, sempre que possí vel, o uso do teorema dos eixos perpendiculares em sua forma geral facilita muito tais determinações.
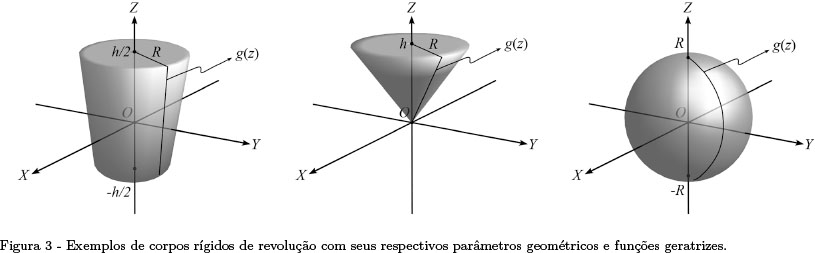
Na Fig. 3, encontram-se esquematizados três sólidos de revolução (cilindro circular reto, cone circular reto e esfera) com seus respectivos parâmetros geométricos, funções geratrizes e os sistemas de eixos em relação aos quais determinaremos IXX e IYY. Para o cilindro, é sabido que V=πR2h e que IZZ=MR2/2 [12]. Assim, como g(z)=R, zmin=-h/2 e zmax=h/2, da Eq. (?) obtemos, após uma integração elementar, o mesmo resultado para 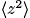 que aparece na Eq. (19) e, portanto, a utilização da Eq. (11) nos dá que
que aparece na Eq. (19) e, portanto, a utilização da Eq. (11) nos dá que
Este resultado foi obtido na Ref. [10] a partir da Eq. (11) e do fato de que o cilindro em questão é um caso particular de um cilindro geral reto. Se R≪ h, a equação acima pode ser escrita como IXX=IYY≈Mh2/12, o que corresponde ao resultado para uma barra delgada [11]. Por outro lado, se R ≫ h teremos um cilindro de altura muito pequena com IXX=IYY≈MR2/4, os quais, juntamente com o valor de IZZ para este cilindro, satisfazem à Eq. (9), como poderí amos esperar.
O próximo exemplo é o cone, que pode ser um bom modelo para um pião e para o qual assumiremos, também, ser conhecido que V=πR2h/3 e que IZZ=3MR2/10 [13]. Como, para o presente caso, g(z)=(R/h)z, zmin=0 e zmax=h, a integral que aparece na Eq. (17) é tão simples como a do exemplo anterior e nos leva à 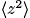 =3h2/5. Conhecendo-se IZZ e tendo chegado a este último resultado, podemos, com o auxí lio da Eq. (11), obter que
=3h2/5. Conhecendo-se IZZ e tendo chegado a este último resultado, podemos, com o auxí lio da Eq. (11), obter que
O caso da esfera que aparece na Fig. 3 é mais simples ainda, pois, devido à sua simetria, podemos utilizar o teorema dos eixos perpendiculares em sua forma expressa pela Eq. (12). Para este caso, V=4πR3/3, g(z) é dada por z2+g(z)2=R2, zmin=-R e zmax=R, resultando da Eq. (17), após uma outra integração elementar, que 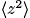 =R2/5. Então, da Eq. (12), obtemos
=R2/5. Então, da Eq. (12), obtemos
Como um último exemplo, vamos determinar os elementos da diagonal do tensor de inércia de um cubo, com arestas de comprimento h, em relação a um sistema de eixos com origem no centro do cubo e com cada um destes eixos perpendicular a cada par de suas faces opostas. Devido à simetria imposta ao sistema pela nossa escolha do sistema de eixos, podemos utilizar, novamente, a Eq. (12) com, agora, 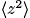 dado pela Eq. (19), pois um cubo é um caso particular de prismas. Portanto, obtemos, imediatamente, que
dado pela Eq. (19), pois um cubo é um caso particular de prismas. Portanto, obtemos, imediatamente, que
Recebido em 24/10/13
Aceito em 23/11/13
Publicado em 6/6/2014
Referências bibliográficas
- [1] M. Alonso e E.J. Finn, Fí sica: Um Curso Universitário, Vol. 1 - Mecânica (Editora Edgard Blücher Ltda., São Paulo, 1994), 1ª ed.
- [2] D. Halliday, R. Resnick e K.S. Krane, Fí sica 1 (Livros Técnicos e Cientí ficos Editora S.A., Rio de Janeiro, 2011), 5ª ed.
- [3] A.P. French, The MIT Introductory Physics Series, Newtonian Mechanics (W.W. Norton & Company Inc., New York, 1971).
- [4] H. Moysés Nussenzveig, Curso de Fí sica Básica, Vol. 1 - Mecânica (Editora Edgard Blücher Ltda., São Paulo, 2011), 4ª ed.
- [5] J.B. Marion and S.T. Thornton, Classical Dynamics of Particles and Systems (Brooks/Cole - Thomson Learning Inc., Pacific Grove CA, 1995), 4ª ed.
- [6] K.R. Symon, Mechanics (Addison-Wesley Publishing Company, Reading MA, 1971), 3ª ed.
- [7] H. Goldstein, Classical Mechanics (Addison-Wesley Publishing Company, Reading MA, 1980), 2ª ed.
- [8] L.D. Landau and E.M. Lifshitz, Course of Theoretical Physics, Vol. 1 - Mechanics (Pergamon Press Ltd., Oxford, 1966), 1ª ed.
- [9] C.J. Coe, Theoretical Mechanics (MacMilian Company, New York, 1938).
- [10] J.P. McKelvey, Am. J. Phys. 51, 658 (1983).
- [11] E.W. Weisstein, Moment of Inertia (MathWorld - A Wolfram Web Resource), http://mathworld.wolfram.com/MomentofInertia.html
- [12] E.W. Weisstein, Cylinder (MathWorld - A Wolfram Web Resource), http://mathworld.wolfram.com/Cylinder.html
- [13] E.W. Weisstein, Cone (MathWorld - A Wolfram Web Resource), http://mathworld.wolfram.com/Cone.html

 O teorema dos eixos perpendiculares para um corpo rígido qualquer
O teorema dos eixos perpendiculares para um corpo rígido qualquer