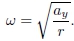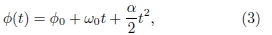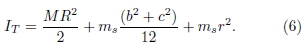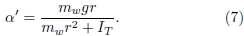Abstracts
The acceleration sensor of a smartphone is used for the study of the uniform and uniformly accelerated circular motions in two experiments. Data collected from both experiments are used for obtaining the angular velocity and the angular acceleration, respectively. Results obtained with the acceleration sensor are in good agreement with alternative methods, like using video recordings of both experiments and a physical model of the second experiment.
rigid solid; mobile application; accele rometer sensor
Neste trabalho foi utilizado o sensor de aceleração de um smatphone em dois experimentos a fim de estudar o movimento circular uniforme e uniformemente acelerado. Os dados coletados em ambos os experimentos foram usados para obter a velocidade angular e a aceleração angular, respectivamente. Os resultados obtidos com o sensor de aceleração apresentam boa concordância com outros métodos alternativos, como usando gravações em vídeo de ambos experimentos e um modelo físico do segundo experimento.
sólido rígido; aplicativo de celulares; acelerômetro
ARTIGOS GERAIS
Using a smartphone acceleration sensor to study uniform and uniformly accelerated circular motions
Uso de um sensor de aceleracão de um smartphone para estudar movimentos circulares uniformes e uniformemente acelerados
Juan C. Castro-PalacioI; Luisberis VelazquezII; José A. Gómez-TejedorIII; Francisco J. ManjónIV; Juan A. MonsoriuV, 1 1 E-mail: jmonsori@fis.upv.es
IDepartment of Chemistry, University of Basel, Switzerland
IIDepartamento de Física, Universidad Católica del Norte, Antofagasta, Chile
IIICentro de Biomateriales e Ingeniería Tisular, Universitat Politècnica de València, València, Spain
IVInstituto de Diseño y Fabricación, Universitat Politècnica de València, València, Spain
VCentro de Tecnologías Fìsicas, Universitat Politècnica de València, València, Spain
ABSTRACT
The acceleration sensor of a smartphone is used for the study of the uniform and uniformly accelerated circular motions in two experiments. Data collected from both experiments are used for obtaining the angular velocity and the angular acceleration, respectively. Results obtained with the acceleration sensor are in good agreement with alternative methods, like using video recordings of both experiments and a physical model of the second experiment.
Keywords: rigid solid, mobile application, accele rometer sensor.
RESUMO
Neste trabalho foi utilizado o sensor de aceleração de um smatphone em dois experimentos a fim de estudar o movimento circular uniforme e uniformemente acelerado. Os dados coletados em ambos os experimentos foram usados para obter a velocidade angular e a aceleração angular, respectivamente. Os resultados obtidos com o sensor de aceleração apresentam boa concordância com outros métodos alternativos, como usando gravações em vídeo de ambos experimentos e um modelo físico do segundo experimento.
Palavras-chave: sólido rígido, aplicativo de celulares, acelerômetro.
1. Introduction
The use of portable devices in all the teaching levels of Physics has increased very fast in the past decade. Various experiments using digital cameras [1], webcams [2], optical mouse of computers [3, 4], wiimote [5], and other game console controllers [6] have been reported. For instance, physical processes can be followed and analyzed by using a simple digital camera [7-9]. The recorded videos can be used to measure time intervals, distances and trajectories of moving objects. Also wireless devices, such as the wiimote, are used in Physics teaching [5, 10, 11]. These devices bear a three-axes accelerometer which communicates with the game console by a bluetooth device.
More recently, smartphones have been incorporated in this variety of portable devices. Specifically, the acceleration sensor of the smartphones has been used for the study of oscillations in simple and coupled oscillations at both qualitative and quantitative levels in high schools [12, 13], and in universities [14, 15], respectively. These works show very simple experiments where the mobile phone itself is the body under study. The oscillations of the acceleration vector captured by the smartphone sensor allow to follow the main features of free, damped and coupled oscillations yielding a very good agreement when compared to traditional experiments.
We present a new application of the smartphone acceleration sensor for the study of the kinematics of the Circular Motion. The topics of Uniform Circular Motion (UCM) and Uniformly Accelerated Circular Motion (UACM) are present in all teaching levels of Physics and pave the ground for the study of more complex rotational motions. There are several experiments reported on this topic [16-22]. For instance, a technique based on 3D video photogrammetry has been used for analyzing a rigid body [19], and the motion of a loaded hoop is studied by using a high-speed video [20]. At the high school level, the radial acceleration in simple experiments (for example in a merry-go-round) has been measured qualitatively with an iPhone [20].
In this work, two experiments for university level students on UCM and UACM are carried out using the data provided by a smartphone acceleration sensor. In the first and second experiments, the angular velocity and the angular acceleration are measured, respectively. Results are compared with alternative methods yielding a good agreement. The outline of the paper is the following. In section II we describe the smartphone acceleration sensor and one of its Android applications. In sections III and IV, the experiments on UCM and UACM are described, respectively. Finally, in section V, some conclusions are drawn.
2. The smartphone acceleration sensor and Android application
In our two experiments, a smartphone Samsung Galaxy S2 bearing an Android version 2.1 and with mass, ms = (0.1350±0.0001) kg was used. The accelerometer sensor is based on three mutually perpendicular silicon circuits, each one oscillating in one direction as a ball hanging on a spring whose movement is restricted to one direction. The accelerometer sensor was controlled by the free Android application "Accelerometer Toy ver 1.0.10". This application takes 154 kB of SD card memory and can be downloaded from Google play website [23]. This application reports the movement of the mobile phone in real time by registering the acceleration components (ax,ay,az) of x,y and z axes as a function of time. The precision in the measurement of the acceleration and time are δa = 0.03 m/s2 and δt = 0.01 s, respectively. This application also allows saving the output data to an ASCII file for further analysis. The structure of the ASCII file is the following. The first column is the order number of the time iteration, the second is the time in miliseconds, and the remaining three columns are the acceleration in x, y and z axes (in m/s2), respectively. Once the application is downloaded to the mobile device, a small test can be performed to proof correct working. It can be proved that when the mobile is left quiet on a horizontal surface, the output curves for the acceleration exhibit values very close to zero for x and y axes, and around 9.8 m/s2 for the z axis.
3. Uniform circular motion
A picture of the setup for this experiment is shown in Fig. 1. The experimental setup consists of a heavy disc of radius R placed in horizontal position which can rotate about the vertical axis passing by its center of mass. For that purpose, the disc is mounted on top of a platform containing a steel bar as vertical axis.
The mobile phone is attached to the disc using double-sided adhesive tape. The objective of the experiment is to measure the angular velocity, ω, of a disc of radius R = (0.114±0.001) m. This is performed by measuring the acceleration with the acceleration sensor, which can be considered as a point located at r=(0.082±0.001) m from the rotation axis. The accelerometer sensor is located at the center of the smartphone. This can be proved by locating the center of the smartphone coincident with the rotation axis. When the disc starts rotating, the acceleration in x- and y-axes is zero, respectively. The z-component of the acceleration equals the gravity (g) whenever the smartphone is placed on the horizontal plane.
In order to start the experiment, a small push is given to the disc to make it rotate, and then is left free. In this way, the y-component of the acceleration represents the centrifugal acceleration while the x-component represents the tangential acceleration. For small time intervals after the initial push, before the friction force appreciably acts on the rotation axis, the angular velocity can be considered constant. This can be seen on the display of the smartphone in the middle line of Fig. 1. The centrifugal acceleration of the acceleration sensor can be expressed as,
from where, the angular velocity can be calculated as,
In Fig. 2, the graphs of the acceleration in the y-axis (ay) versus time are shown for two trials of increasing values of the angular velocity. The angular velocity is calculated by taking the time average over the first second after the push. It can be seen in Fig. 2 that ay is approximately constant.
The angular velocity is also calculated from the analysis of the video recording of the experiment. The time elapsed for each lap, which is the period (τ), is used to calculate the angular velocity as ω=2π/τ. The values of the angular velocities for the first four laps are averaged to obtain the reported value in Table 1 in comparison with the values obtained from the accelerometer sensor data. The uncertainties and the percentage discrepancies for each case are also shown in this table.
4. Uniformly accelerated circular motion
The experimental setup used to measure the angular acceleration is shown in Fig. 3a. The same rotatory disc as for the previous experiment is used, but this time its axis is connected by a pulley attached to it to another pulley placed vertically. Thus, the rotatory motion of the disc is connected to the translational motion of a suspended weight of mass mw by means of an inextensible string. The masses of the pulleys and the string are considered negligible. Once the suspended body is left free, the disc starts moving with an approximately constant angular acceleration. For comparison, the angular acceleration, α, is also calculated from the analysis of the video recording of the experiment and from a physical model based on the Newton's equations.
4.1. Angular acceleration calculated from the acceleration sensor data
The response of the y-component of the acceleration measured by the acceleration sensor versus time is plotted in Fig. 4a for a mass, mw = 200 g of the suspended body. The centrifugal acceleration for the UACM is expressed as,
Assuming an initial angular velocity ω0=0 in Eq.(1), we get,
The acceleration sensor data versus time is fitted to Eq. (2) and one example of the curves is shown in Fig. 4a. The angular acceleration is obtained as the fitting parameter using the Levenberg-Marquardt non-linear fitting algorithm [24]. The potential growth of ay can be also seen on the smartphone display in Fig. 3b (line indicated with an arrow). The origin of the coordinate system of the acceleration curves can be observed in Fig. 3b.
4.2. Angular acceleration calculated from the video analysis
The angular acceleration can be also calculated from the video recording of the experiment. The time at each π/2 for angle of rotation ϕ(t), is measured by editing the video with Windows Movie Maker software on Windows Operating System, which allows a precision of 0.04 s. The angle of rotation for the UACM as a function of time is calculated as,
where ϕ0 = 0 and ω0 = 0 are the initial angular position and initial angular velocity, respectively. The values of ϕ(t) are plotted versus t2 to obtain the angular acceleration from the slope. In Fig. 4b, the results of the linear fit are shown for the mass, mw = 200 g of the suspended body. The data points are also included. The resulting angular accelerations are shown in Table 2.
4.3. Angular acceleration calculated from the Newton's equations
The angular acceleration can be also obtained from Newton's equations. Let us write the Newton's second equation for the suspended body and for the rotating disc holding the mobile device on top. The equation for the translation of the suspended body is,
where T is the tension force of the string (considered massless and inextensible) and a is the linear acceleration of the suspended body. The equation for the rotation of the disc (including the mobile device) is,
where rp=(0.015±0.001) m is the radius of the co-axial pulley attached to the disc just below it, α' is the angular acceleration, and IT, is the total moment of inertia, which includes the moment of the inertia of the disc and of the smartphone,
In the equation above, M = (1.3550±0.0001) kg is the mass of the disc, R is its radius, ms is the mass of the smartphone, r= (0.082±0.001) m is the distance of the sensor from the axis, and b = (0.125±0.001) m and c= (0.065±0.001) m are the lengths of the sides of the mobile phone considered with rectangular shape. The first term in Eq. (6) indicates the moment of inertia of the disc and the second and third terms, the moment of inertia of the mobile. The latter is calculated using the expression to calculate the moment of inertia of a rectangular prism about its center  and the Steiner's theorem of parallel axes
and the Steiner's theorem of parallel axes  . Combining Eqs. (4), (5), and (6), and setting a=α'r, we get an expression to calculate the angular acceleration,
. Combining Eqs. (4), (5), and (6), and setting a=α'r, we get an expression to calculate the angular acceleration,
In Table 2, the values of the angular acceleration as calculated from the smartphone acceleration sensor data, from the analysis of the video recording of the experiment, and from the physical model based on the Newton's equations are shown. In the first and second cases, an average of the angular acceleration over three trials was considered. As for the error, the average standard deviations of the data were considered.
5. Conclusions
The UCM and UACM are studied by means of two experiments using the smartphone acceleration sensor. The results for the angular velocity and the angular acceleration of UCM and UACM, respectively, are compared to those obtained with alternative methods, that is, the analysis of the video recordings of the first and second experiment, and with a physical model in the second experiment. The discrepancies between the results obtained from the acceleration sensor data and from the alternative methods are less than 2 % for the UCM, and less than 5 % for the UACM, thus showing the ability of the acceleration sensor of the smartphone for this type of measurements. In summary, it has been shown that using a smartphone, a very familiar device to Physics' students, it is possible to perform very simple experiments and capture the quantitative features of uniform and uniformly accelerated circular motions.
Acknowledgments
The authors would like to thank the Institute of Education Sciences, Universitat Politècnica de València (Spain), for the support of the Teaching Innovation Groups, MoMa and e-MACAFI.
Recebido em 7/11/13
Aceito em 24/2/14
Publicado em 6/6/2014
- [1] J.A. Monsoriu, M.H. Giménez, J. Riera and A. Vidaurre, Eur. J. Phys. 26, 1149 (2005).
- [2] S. Shamim, W. Zia and M.S. Anwar, Am. J. Phys. 78, 433 (2010).
- [3] O.O. Romulo and K.N. Franklin, Am. J. Phys. 65, 1115 (1997).
- [4] T.W. Ng and K.T. Ang, Am. J. Phys. 73, 793 (2005).
- [5] S.L. Tomarken, D.R. Simons, R.W. Helms, W.E. Johns, K.E. Schriver et al., Am. J. Phys. 80, 351 (2012).
- [6] M. Vannoni and S. Straulino, Eur. J. Phys. 28, 781 (2007).
- [7] H.C. Chung, J. Liang, S. Kushiyama and M. Shinozuka, Int. J. Non-Linear Mech. 39, 691 (2004).
- [8] T. Greczylo and E. Debowska, Eur. J. Phys. 23, 441 (2002).
- [9] C. Sirisathitkul, P. Glawtanong, T. Eadkong and Y. Sirisathitkul, Rev. Bras. Ensino Fis. 35, 1504 (2013).
- [10] A. Kawam and M. Kouh, Phys. Teach. 49, 508 (2011).
- [11] R. Ochoa, F.G. Rooney and W.J. Somers, Phys. Teach. 49, 16 (2011).
- [12] P. Vogt and J. Kuhn, Phys. Teach. 50, 439 (2012).
- [13] J. Kuhn and P. Vogt, Phys. Teach. 50, 504 (2012).
- [14] J.C. Castro-Palacio, L. Velazquez-Abad, M.H. Gimenez and J.A. Monsoriu, Am. J. Phys. 81, 472 (2013).
- [15] J.C. Castro-Palacio, L. Velazquez-Abad, F. Gimenez and J. A Monsoriu, Eur. J. Phys. 34, 737 (2013).
- [16] E. Butikov, Eur. J. Phys. 27, 913 (2006).
- [17] S. Zabunov, Eur. J. Phys. 31, 1345 (2010).
- [18] K. Kassner, Am. J. Phys. 80, 772 (2012).
- [19] A. Page, P. Candelas, F. Belmar and H. De Rosario, Am. J. Phys. 75, 56 (2007).
- [20] M.F. Maritz and W.F.D. Theron, Am. J. Phys. 80, 594 (2012).
- [21] P. Vogt and J. Kuhn Phys. Teach. 51, 182 (2013).
- [22] N. Beraha, M.F. Carusela and C.D. El Hasi Rev. Bras. Ensino Fis. 31, n. 4, 4503 (2009).
- [23] https://play.google.com/store/apps
» link - [24] D. Marquardt, SIAM J. Appl. Math. 11, 431 (1963).
Publication Dates
-
Publication in this collection
03 July 2014 -
Date of issue
June 2014
History
-
Accepted
24 Feb 2014 -
Received
07 Nov 2013