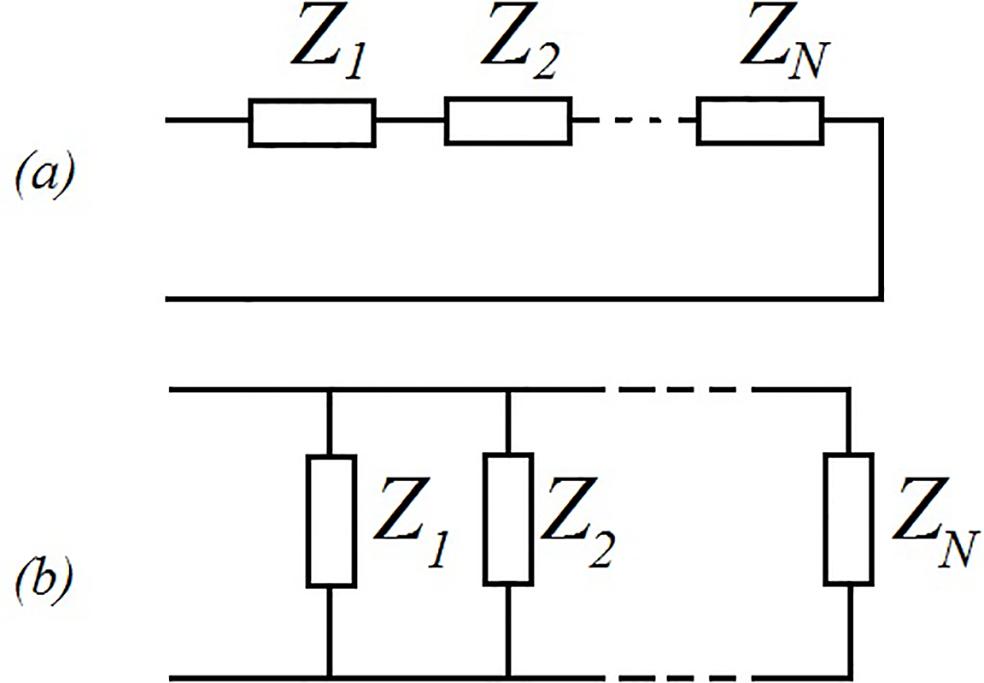Resumo
A geometria fractal fascina pela capacidade de descrever formas geométricas complexas e que usualmente estão presentes no mundo real . A dimensão fractal ou de Hausdorff d é utilizada para descrever leis de invariância de escala, em que as funções autossimilares seguem uma lei da forma , sendo s o fator de escala. Intimamente relacionado ao problema da invariância de escala está o problema da determinação dos pontos fixos de um sistema, que matematicamente correspondem aos pontos que mapeiam o domínio de uma função para ele mesmo. Em sistemas dinâmicos correspondem ao valor para o qual a resposta do sistema usualmente converge e permanece estável. Na presente contribuição são apresentados os conceitos gerais associados à invariância de escala e ponto fixo, para prontamente empregá-los no problema de associação de impedâncias complexas em série e em topologia de escada. São discutidos em detalhes o problema da função de transferência de linhas de transmissão e o estudo de alguns gráficos de fluxo (flow graphs) de convergência das equações de recursividade.
Palavras-chave:
circuitos elétricos; linhas de transmissão; dimensão de Hausdorff; invariância de escala; fractais
Abstract
Fractal geometry is fascinating due to its ability to describe the complex geometries naturally occurring in real world. The fractal or Hausdorff dimension d is used to describe the laws of scale invariance, which are exemplified by functions satisfying a mathematical law of the form , being s the scale factor. Closely related is the problem of determining the fixed point of physical systems. Mathematically, the fixed point corresponds to a point in the domain of a function which is mapped to itself. In dynamical systems, it typically corresponds to the value to which the response of the system converge and stabilize. The present contribution aims to present the general concepts of scale invariance and fixed or critical points, employing such aspects to the problem of complex impedance association, both in series and in ladder configuration. The complex impedance, and transfer function of transmission lines and flow graphs related to the convergence the iterative equations to a fixed points are discussed in more details.
Keywords:
electric circuits; transmission lines; Hausdorff dimension; scale invariance; fractals
1. Introdução
O fascínio exercido pela geometria fractal pode ser atribuído ao fato de que ela é capaz de descrever matematicamente as formas geométricas que ocorrem na natureza, indo desde as formas biológicas como árvores e plantas em geral, alvéolos pulmonares e a capilaridade dos vasos sanguíneos no corpo humano, passando pela descrição dos flocos de neve, das formas de montanhas, contornos de relevo e costas dos países, e chegando à escala astronômica das galáxias e aglomerados. Um fractal é um objeto cuja dimensão efetiva denominada de dimensão de Hausdorff-Besicovitch excede aquela dada pela topologia do espaço onde está embutido, sendo esta dimensão topológica inteira [1[1] B.B. Mandelbrot, The Fractal Geometry of Nature (W. H. Freeman and Company, New York, 1982). [2] B. Mandelbrot, Science 156, 636 (1967). [3] G. Edgar, Measure, Topology, and Fractal Geometry (Springer Science & Business Media, Berlim, 2007). [4] N. Gordon, Introducing fractal geometry (Icon Books, London, 2000). [5] R.S. Strichartz, Differential equations on fractals: a tutorial (Princeton University Press, Nova Jersey, 2006). [6] J.F. Gouyet, Physics and fractal structures (Masson Springer, New York, 1996). [7] H. Takayasu, Fractals in the Physical Sciences (Manchester Univ. Press, Manchester, 1990). [8] T. Nakayama, K. Yakubo and R. L. Orbach, Rev. Mod. Phys. 66, 381 (1994).-9[9] A. Lesne e M. Laguës, Scale Invariance: From phase transitions to Turbulence (Springer-Verlag, Berlin, 2012).]. Como já é de amplo conhecimento, o nome fractal deve-se ao matemático polonês Benoit Mandelbrot, também naturalizado americano e francês, que utilizou a raiz etimológica do latim fractus em 1975 para significar objeto fraturado ou quebrado. Nas palavras do próprio Mandelbrot, ``Nuvens não são esferas, montanhas não são cones, linhas costeiras não são círculos, uma superfície não é suave e um raio não viaja em linha reta", na introdução ao seu livro The Fractal Geometry of Nature, de 1982 [1][1] B.B. Mandelbrot, The Fractal Geometry of Nature (W. H. Freeman and Company, New York, 1982)..
Embora não seja condição necessária para a definição de fractais em geral, um aspecto muito interessante de ampla gama de estruturas fractais é o conceito de autossimilaridade, que corresponde à relação de semelhança que uma parte do objeto tem com o todo [9][9] A. Lesne e M. Laguës, Scale Invariance: From phase transitions to Turbulence (Springer-Verlag, Berlin, 2012).. Dito de outra forma, a estrutura fractal se repete em escalas diferentes. Nesse contexto as estruturas fractais têm sido estudadas há muito tempo e um dos pioneiros foi Gottfried Leibniz, com seus estudos sobre formas autossimilares recursivas e expoentes fracionários [10[10] K.S. Miller e B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations (John Wiley & Sons, New York, 1993).,11[11] K.B. Oldham e J. Spanier, The Fractional Calculus: Theory and Aplications, Differentiation and Integration to Arbitrary Order (Academic, New York, 1974).] ainda no século XVII.
No século XIX foram importantes os trabalhos de Karl Weierstrass, com a descoberta da função que leva seu nome e apresenta autossimilaridade em escalas distintas, é contínua e não diferenciável [12[12] G.H. Hardy, Transactions of the American Mathematical Society 17, 301 (1916).,13[13] B.R. Hunt, Proceedings of the American Mathematical Society 126, 791 (1998).], e também de Georg Cantor, com a discussão do conjunto de Cantor, sabidamente hoje um tipo de fractal [14][14] T.A. de Assis, J.G.V. Miranda, F.B. Mota, R.F.S. Andrade e C.M.C. de Castilho, Revista Brasileira de Ensino de Física 30, 2304 (2008).. Também são dignos de nota os trabalhos de Henri Poincaré sobre o que veio a ser conhecida como a teoria do caos, descrevendo sistemas dinâmico que é particularmente sensível às condições iniciais, onde um conjunto de pontos da resposta do referido sistema para onde a solução parece convergir, denominado de atrator, apresentam aspecto fractal[1][1] B.B. Mandelbrot, The Fractal Geometry of Nature (W. H. Freeman and Company, New York, 1982).. No século XX, além do trabalho de Mandelbrot, devemos mencionar as curvas de Koch [15][15] H. Sagan, Space-Filling Curves (Springer-Verlag, New York, 1994). e o modelo geométrico para o floco de neve, o triângulo de Sierpinski [9][9] A. Lesne e M. Laguës, Scale Invariance: From phase transitions to Turbulence (Springer-Verlag, Berlin, 2012)., os conjuntos de Fatou-Julia, utilizando funções complexas [16[16] G. Julia, Journal de Mathématiques Pures et Appliquées 8, 47 (1918). [17] P. Fatou, Comptes Rendus de l'Académie des Sciences de Paris 164, 806 (1917).-18[18] T. Lei, Communications in Mathematical Physics 134, 587 (1990).], e a definição fundamental de dimensão fractal feita pelo matemático Felix Hausdorff [19][19] F. Hausdorff, Mathematische Annalen 79, 157 (1919). e avançada pelo russo Abram Samoilovitch Besicovitch [20[20] A.S. Besicovitch, Mathematische Annalen 101, 161 (1929).,21[21] A.S. Besicovitch e H.D. Ursell, Journal of the London Mathematical Society 12, 18 (1937).] . Estudando curvas autossimilares e caminhos randômicos Paul Levy inaugurou o ramo dos vôos de das distribuições de Levy, que apresentam dimensão fractal, tendo grande impacto sobre o campo da estatística [22][22] V. Zaburdaev, S. Denisov e J. Klafter, Rev. Mod. Phys. 87, 483 (2015)..
Atualmente, vários conceitos da geometria fractal têm sido utilizados na Física e na Engenharia para descrever processos ou estruturas autossimilares e fenômenos cuja resposta apresente uma lei de potência fracionária, indo desde a descrição do comprimento de polímeros até o comportamento de dispositivos semicondutores [23[23] C. Vijayan e M. Ravikumar, J. Chem. Educ. 70, 830 (1993).
[24] S. Havlin e D. Ben-Avraham, J. Phys. A: Math. Gen. 15, L311 (1982).
[25] K. Tsujii, Polymer Journal 40, 785 (2008).
[26] J.P. Chen, S. Molchanov e A. Teplyaev, Journal of Physics A: Mathematical and Theoretical 48, 395203 (2015).
[27] E. Akkermans, G.V. Dunne e A. Teplyaev, Europhysics Letters 88, 40007 (2009).
[28] E. Akkermans, G.V. Dunne e A. Teplyaev, Phys. Rev. Lett. 105, 230407 (2010).
[29] S. Alexander e R. Orbach, Journal de Physique Lettres 43, 625 (1982).
[30] Y. Gefen, A. Aharony e S. Alexander, Phys. Rev. Lett. 50, 77 (1983).
[31] https://ieeexplore.ieee.org/abstract/document/6229091
https://ieeexplore.ieee.org/abstract/doc...
[32] Y. Chen, PLoS ONE 6, e24791 (2011).-33[33] M.K. Hassan e G.J. Rodgers, Physics Letters A 208, 95 (1995).] e o grupo de renormalização em teorias quânticas de campos e estudo de transições de fase [34[34] J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford University Press, Reino Unido, 2002).,35[35] F. Englert, J.M. Frère, M. Rooman e P. Spindel, Nuclear Physics B 280, 147 (1987).]. Em Engenharia Eletromagnética, sobretudo no espectro das micro-ondas (faixa de frequências compreendida entre 300 MHz e 300 GHz no espectro de radiofrequências), a ideia de ocupar melhor a área disponível tem permitido miniaturizar os circuitos elétricos através do projeto de antenas, acopladores e filtros fractais, o que é essencial para a redução das dimensões físicas de telefones móveis, notebooks e circuitos de identificação por radiofrequência (RFID) [36[36] S.R. Best, IEEE Antennas and Wireless Propagation Letters 1, 74 (2002).
[37] S.R. Best, IEEE Antennas and Wireless Propagation Letters 2, 197 (2003).
[38] R. Hohlfeld e N. Cohen, Fractals 7, 79 (1999).
[39] J.P. Chen, L.G. Rogers, L. Anderson, U. Andrews, A. Brzoska, A. Coffey, H. Davis, L. Fisher, M. Hansalik, S. Loew e A. Teplyaev, J. Phys. A: Math. Theor. 50, 325202 (2017).
[40] P. Alonso-Ruiz, J. Math. Phys. 58, 073503 (2017).
[41] S.H. Yoon, European Journal of Physics 28, 277 (2007).
[42] B. Boyle, K. Cekala, D. Ferrone, N. Rifkin e A. Teplyaev, Pacific Journal of Mathematics 233, 15 (2007).
[43] C. Ucak, European Journal of Physics 30, 945 (2009).
[44] P. Jarry e J. Beneat, Design and Realizations of Miniaturized Fractal RF and Microwave Filters (Wiley, USA, 2009).-45[45] https://bit.ly/2OqoDVE.
https://bit.ly/2OqoDVE...
].
Já há na própria Revista Brasileira de Ensino de Física um trabalho abordando os conceitos fundamentais da geometria fractal, discutindo de forma rigorosa o cálculo da dimensão fractal de várias estruturas [14][14] T.A. de Assis, J.G.V. Miranda, F.B. Mota, R.F.S. Andrade e C.M.C. de Castilho, Revista Brasileira de Ensino de Física 30, 2304 (2008).. A presente contribuição tem por objetivo apresentar de forma didática, através de exemplos concretos em circuitos elétricos, a aplicação de aspectos de autossimilaridade e dimensão fractal. Para tanto, na Seção 2 serão apresentados os conceitos fundamentais de autossimilaridade e transformação de escala em funções e dimensão de Hausdorff-Besicovitch. Na Seção 3, para facilitar a compreensão do presente trabalho sem a necessidade de recorrer a uma literatura adicional, os aspectos fundamentais da teoria de funções resposta serão colocados. Na Seção 4, alguns circuitos elétricos e dispositivos de micro-ondas autossimilares serão analisados. Finalmente, na Seção 5 as conclusões gerais serão apresentadas.
2. Invariância de Escala e Dimensão de Hausdorff
O conceito de invariância de escala é um dos mais importantes na Física moderna, sendo empregado em uma vasta gama de problemas, indo desde a análise da solução de problemas não-lineares, como as equações de Navier-Stokes até o problema de renormalização na teoria quântica de campos[46[46] W.D. McComb, Renormalization Methods: A Guide For Beginners (Oxford University Press, USA, 2008).,47[47] J. Zinn-Justin, Phase Transitions and Renormalization Group (Oxford University Press, USA, 2013).]. Uma estrutura invariante de escala é aquela que preserva a similaridade com ela mesma quando observada de escalas distintas. Um objeto invariante de escala verdadeiro repete sua forma em todas as escalas e possui, portanto, uma complexidade infinita. Alguns fenômenos importantes associados à invariância de escala são as transições de fase e as classes de universalidade, onde fenômenos aparentemente distintos como o comportamento da transição do estado ferromagnético para o estado paramagnético no modelo de Ising próximo da temperatura crítica e a transformação de fase líquido-gás perto do ponto crítico podem apresentar leis de potências similares e expoentes críticos idênticos [9[9] A. Lesne e M. Laguës, Scale Invariance: From phase transitions to Turbulence (Springer-Verlag, Berlin, 2012)., 46[46] W.D. McComb, Renormalization Methods: A Guide For Beginners (Oxford University Press, USA, 2008).].
Para compreender a lei da invariância de escala matematicamente considere uma função f(x) dependente de uma variável x que pode ser redimensionada para s x, sendo s o fator de escala. A invariância de escala requer que a função reescalonada f(sx) tenha a mesma forma de f(x), a menos de um fator multiplicativo e dependente da escala escolhida, na forma:
onde d é a dimensão fractal, com a qual efetivamente a função varia de tamanho. Podemos calcular o expoente d da transformação simplesmente reescrevendo a equação acima na forma e então tomando o logarítmo (em qualquer base que se queira) em ambos os lados. O resultado é a dimensão de Hausdorff-Besicovitch:
É importante notar que ao considerarmos uma estrutura autossimilar, é possível escolher um tal fator de escala que faça a relação , sendo N o número de cópias da estrutura original obtida no processo de reescalonamento com fator de escala s. Nesse caso a dimensão fractal é dada pela seguinte fórmula:
Deve-se distinguir aqui o conceito de dimensão topológica do conceito de dimensão de Hausdorff. Sem buscar uma definição rigorosa do ponto de vista matemático, grosso modo a dimensão topológica refere-se ao número de eixos (ou variáveis) do espaço em que o objeto está embutido, sendo um número inteiro para os espaços euclidianos e também para os espaços de Minkowski. Por outro lado, a dimensão fractal é uma medida de preenchimento do espaço topológico, e é dada pelo expoente d do fator de escala s com o qual a função ou estrutura embutida no espaço topológico deve ser escalonada ao realizarmos uma mudança na escala das dimensões topológicas.
Utilizando a definição (2) fica claro que as funções monomiais, da forma , tem dimensão de Hausdorff-Besicovitch sendo qualquer número. Se consideramos uma função linear representando um comprimento físico de uma linha, a dimensão fractal será igual à dimensão topológica. Sabemos da geometria euclidiana que a reta tem dimensão . Tomando uma linha de comprimento x podemos aplicar um fator de escala e o novo comprimento será . Claramente agora temos objetos de tamanho x, e aplicando a fórmula (3) obtemos a dimensão fractal .
Na sequência podemos considerar uma função quadrática representando a área de um quadrado. Ao aplicarmos o mesmo fator de escala de antes, obteremos . Isso significa que temos agora réplicas idênticas do quadrado original de tamanho . A aplicação da expressão para a dimensão de Hausdorff produz . Como sabemos, um quadrado tem dimensão na geometria euclidiana. Aplicando a mesma ideia a um cubo de aresta x cujo volume vale , o reescalonamento por um fator , produz cubos idênticos (autossimilares) ao cubo original, e nesse caso , conforme esperado.
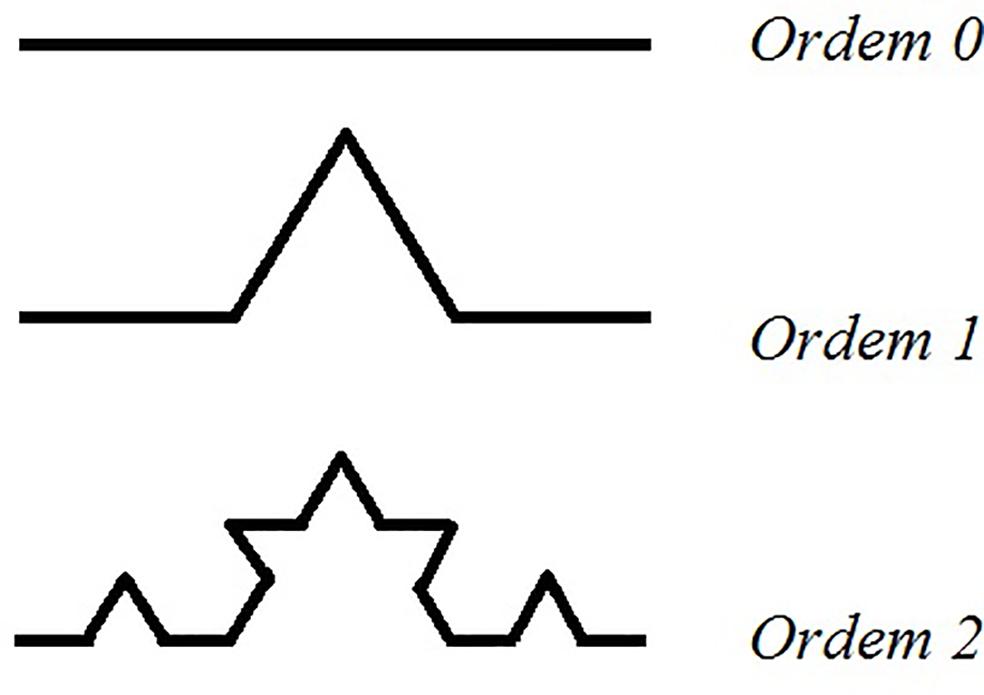
Com a finalidade de compreender um pouco melhor o procedimento de determinação da dimensão de Hausdorff em uma estrutura autossimilar, considere primeiro a curva de Koch, ilustrada em seu processo inicial de construção na Figura 1. Na ordem 0 temos uma reta de comprimento x. Para a obtenção da ordem 1 a reta original é seccionada em 3 partes idênticas. Então é construido um novo objeto com 4 cópias do segmento de comprimento . Desse modo, temos enquanto que para obter um objeto do tamanho original x a partir de uma parte precisamos reescalonar por um fator . A ordem 2 é obtida realizando o mesmo procedimento, mas agora no objeto de ordem 1. Teremos agora, em relação ao objeto original cópias idênticas da reta x, com fator de escala . O processo continua e temos e na ordem n-ésima. A dimensão fractal da curva de Koch no limite será dada simplesmente por .
A Curva de Kock em ordem 0, 1 e 2. Para a obtenção de um fractal verdadeiro o processo deve prosseguir com .
Como segundo exemplo, considere o triângulo de Sierpinski. A partir do triângulo equilátero de ordem 0, divide-se o lado desse por um fator 2. O próximo passo é remover do centro do triângulo original a área de um triângulo equilátero de lado , conforme ilustrado na Figura 2, restando assim 3 triângulos idênticos de lado . Assim, o número de cópias do objeto original é , mas para obter o triângulo original a partir do reescalonamento de um dos triângulos menores precisamos aplicar um fator de escala no tamanho da aresta. Na próxima etapa, fazemos a remoção de um triângulo no centro de cada triângulo menor, o que corresponde a obter cópias do triângulo original, mas cada um com lado , e portando o fator de escala a ser aplicado será . Na ordem n-ésima do processo teremos triângulos idênticos ao original, que pode ser obtido por um fator de escala aplicado a um dos objetos menores. Podemos tomar o limite e calcular ao final a dimensão fractal, que nesse caso será dada por . É importante destacar ainda a diferença entre a geometria fractal matemática ideal, que pressupõe complexidade infinita com , e os fractais que ocorrem naturalmente ou empregados em sistemas físicos reais, que são sempre truncados (n é finito) e perdem o caráter autossimilar a partir de uma certa escala de tamanhos.
Agora se faz necessária a distinção entre os fractais artificiais e os fractais ``naturais". Um fractal artificial, aquele gerado matematicamente, é autossimilar e possui complexidade infinita. A ampliação de um fragmento terá exatamente a mesma forma do todo. Como exemplos, podemos mencionar os fractais discutidos aqui discutidos anteriormente (Curva de Koch e Triângulo de Sierpinski). Já os fractais que ocorrem naturalmente, como as árvores, linhas costeiras, ou superfícies reais, apresentam algums propriedades de autossimilaridade apenas de forma estatística. A ampliação de uma parte pode não ser autossimilar ao objeto completo, mas apresentam estatisticamente aspectos de autossimilaridade. Dentro desse conceito de fractais estatisticamente autossimilares, define-se a auto-afinidade. Nas estruturas auto-afins o fator de escala é distinto nas diversas direções topológicas. Por exemplo, em duas dimensões topológicas (), o fator de escala pode ser diferente do fator de escala para uma função . Os fractais estatisticamente autossimilares (ou auto-afins) podem não ser simétricos, e a forma correta de calcular a lei de escala se dá através do uso de expoentes de Hurst, o que vai além do escopo do presente trabalho. É importante destacar ainda que os fractais naturais não apresentam complexidade infinita, em contraste com os fractais definidos matematicamente. Ainda assim, são considerados fractais quando o resultado experimental obedece a uma lei de escala por pelo menos três ordens de magnitude.
Para finalizar a presente Seção, vamos discutir o problema do ponto fixo, muito importante sobre tudo no estudo de transições de fase. Considere um objeto sujeito a uma lei de iteração, tal que o valor (ou a forma) de depende de uma função do valor anterior, . Esse tipo de processo estocástico é denominado de cadeia de Markov, onde o resultado atual somente depende do estado anterior do sistema. Matematicamente temos a relação de recursividade:
Alcançamos um ponto fixo do sistema quando e a solução desse sistema não varia mais. Para encontrar o ponto fixo precisamos resolver uma equação do tipo , que normalmente são transcendentais nos sistemas físicos de interesse. Na teoria do campo médio a equação para resolver a magnetização do sistema na aproximação de Curie-Weiss toma a forma típica , onde é a magnetização normalizada pelo valor de saturação e é o recíproco da temperatura, normalizada pela temperatura crítica do sistema ( ).
Os pontos fixos podem der classificados em atrativos, quando dado um valor inicial a solução converge para esse ponto fixo, ou repulsivos, quando dado um inicial próximo do ponto fixo, a solução se afasta desse ponto. Como exercício simples, considere a equação recursiva na forma abaixo:
cuja equação de ponto fixo fica na forma o que implica , tendo dois pontos fixos e .
Na Figura 3 mostramos o mapa de convergência das soluções para distintos valores da condição inicial . Foram escolhidos os valores , logo acima do ponto fixo , que é um ponto repulsivo, e valores de no intervalo , que é denominada área ou bacia de atração do ponto fixo . Nesse intervalo a solução converge para se o número de iterações é levado ao infinito, , não importanto o valor inicial escolhido, desde que dentro da área de atração daquele ponto. Um ponto fixo atrator é um ponto de solução de equilíbrio estável do sistema, enquanto que um repulsor é uma condição de equilíbrio instável e qualquer flutuação do sistema o tirará desta condição.
Convergência da equação , para algumas condições iniciais após 12 iterações. Os pontos fixos são (atrator) e (repulsor).
3. Fundamentos da Teoria da Função Resposta de um Sistema
A causalidade é o princípio fundamental que guia a descrição dos sistemas físicos reais. Restringindo a atenção a sistemas lineares, não é satisfatória qualquer modelagem matemática de um sistema físico em que o efeito não seja precedido por uma fonte que lhe sirva de estímulo ou força motriz. No domínio do tempo em sistemas lineares a relação de causalidade entre a saída e o estímulo que lhe deu origem está muito bem representada por uma integral de convolução, na forma abaixo:
onde é denominada tipicamente de função resposta no domínio do tempo, resposta ao impulso de Dirac ou ainda função de Green do sistema. Esta última denominação é mais comum entre físicos e matemáticos, enquanto as outras são mais frequentemente empregadas por engenheiros. O leitor deve observar que a saída no instante de tempo t pode depender de todos os estímulos que ocorreram em instantes de tempo anteriores a ao instante t e por esse motivo a função deve ser nula para qualquer instante , o que significa que não haverá uma resposta do sistema sem que haja primeiro um estímulo.
Em um sistema com múltiplas entradas e múltiplas saídas a equação para a -ésima saída deve depender da -ésima entrada na forma abaixo:
Nesse caso são os elementos de uma matriz . Fazendo uso das transformadas de Fourier, entre os domínios duais de tempo t e frequência angular temporal , definidas conforme abaixo:
pode-se obter a seguinte relação (através do teorema da convolução):
que significa que a convolução no domínio do tempo entre o estímulo e a função de Green do sistema é transformada em um simples produto dessas funções no domínio da frequência. Aqui a função de Green é dada por:
sendo também denominada de função de transferência, ganho ou susceptibilidade do sistema, a depender do contexto. Na maioria dos problemas físicos lineares é mais fácil obter a função resposta diretamente no domínio da frequência angular temporal .
Um sistema físico qualquer pode ser descrito por uma equação diferencial dada na forma abaixo:
onde e são coeficientes constantes e reais. Note que aqui as derivadas da saída são relacionadas às derivadas do estimulo. Podemos aplicar a seguinte propriedade da transformada de Fourier para funções de suporte compacto (i.e., que tendem para zero em ):
e então obter a função resposta no domínio da frequência em forma de divisão entre polinômios:
Vamos lembrar ao leitor que os elementos passivos fundamentais de circuitos elétricos, com os quais se pode construir modelos de sistemas mais complexos, são resistores, capacitores e indutores. As leis que governam asrelações entre a tensão V e a corrente elétrica I nesses elementos, tanto no domínio do tempo quanto na frequência, são dadas a seguir:
onde (15), (16) e (17) são as equações que definem a lei do resistor, do capacitor e do indutor, respectivamente, R é a resistência elétrica, medida em ohms no SI, C é a capacitância elétrica, medida em farad no SI, e L é a indutância, medida em henry no SI. Note o papel dual desempenhado por indutores e capacitores.
Para concluir essa Seção com um exemplo didático vamos considerar o caso de um circuito RC série, conforme ilustrado na Figura 4. A equação diferencial que governa esse sistema é dada abaixo:
onde é a constante de tempo desse circuito. Quando levado para o domínio da frequência angular temporal ω, o ganho tem a seguinte expressão:
Para trazer novamente para o domínio do tempo e obter , podemos simplesmente fazer a transformada de Fourier inversa:
onde é utilizado o teorema do resíduo de Cauchy para obter o resultado desejado. A função é o degrau de Heaviside, sendo nula para e unitária para .
A função do denominador deve ser colocada na forma . Para o caminho de integração no plano complexo é fechado no semi-plano superior (ver Figura 5), fazendo envolver o pólo enquanto que para o caminho de integração é fechado pelo semi-plano inferior, não envolvendo o pólo produzindo resultado nulo na integral.
O caminho de integração para a equação (20) no plano complexo. Para o caminho é fechado no semi-plano superior, envolvendo o pólo .
Com relação à invariância de escala da função resposta desse circuito RC série podemos perceber que ao fazer uma transformação de escala no tempo para , devemos reescalonar para e nesse caso . Uma vez que o tempo e a frequência são variáveis duais do ponto de vista da transformada de Fourier, a nova escala de tempo produz um reescalonamento no domínio da frequência na forma .
Para frequências tais que a função toma a forma monomial . Nesse regime a função é invariante de escala pela transformação , na forma da equação (1), com expoente . Funções resposta de circuitos RC fracionários, ou seja, com expoentes fracionários para , foram consideradas na Ref. [48][48] A.M.F. de Andrade, E.G. de Lima e C.A. Dartora, Revista Brasileira de Ensino de Fí-sica 40, e3314 (2018)..
4. Circuitos Elétricos e a Linha de Transmissão
A ideia de utilizar estruturas fractais na engenharia de dispositivos eletromagnéticos e circuitos elétricos tem sido considerada atrativa em dois aspectos: i) com a utilização de curvas de preenchimento do espaço (space filling curves), é possível otimizar o aproveitamento da área disponível e miniaturizar os circuitos elétricos, os filtros e os acopladores em micro-ondas; ii) obtenção de funções de transferência com expoentes efetivamente fracionários, o que permite manipular a largura de banda de filtros e casadores de impedância, tão fundamentais nos projetos de circuitos eletrônicos. Várias dessas ideias podem ser prontamente aplicadas no desenvolvimento de sistemas mecânicos análogos ou também na modelagem efetiva de meios materiais que apresentam respostas com relaxação seguindo uma lei de potência , ao invés de uma lei exponencial .
Circuitos elétricos puramente resistivos apresentando a auto-similaridade e a invariância de escala foram considerados na Ref. [49][49] C.X.M. dos Santos, C.M. Mendes e M.V. Freire, Revista Brasileira de Ensino de Física 40, e1302 (2018)., utilizando a teoria de grafos. Lá foram explorados o caso de uma associação em série de infinitos resistores e também o arranjo do triângulo de Sierpinski.
Aqui vamos generalizar o problema, considerando a impedância e a função de transferência para o caso de uma associação de impedâncias complexas. O problema de uma linha de transmissão será abordado pelo prisma da invariância de escala em um circuito do tipo escada. A impedância de um circuito, medida em ohms no SI, é a razão entre a tensão elétrica e a corrente elétrica que circula pelo elemento, no domínio de frequência:
O inverso de uma impedância é denominado de admitância do circuito.
Dois casos de particular interesse, úteis na análise que segue, são a associação em série e em paralelo de impedâncias, conforme ilustrado na Figura 6. A impedância equivalente na associação de N impedâncias em série é dada pela soma das impedâncias na forma abaixo:
enquanto que no caso da associação paralela é melhor trabalhar com as admitâncias:
Para elementos resistivos (R), capacitivos (C) e indutivos (L) ideais, as impedâncias são dadas por , e , respectivamente. No circuito RC em série, por exemplo, já discutido anteriormente, a impedância equivalente é dada por .
4.1. Associação Em Série de Impedâncias Autossimilares
Consideremos uma rede de impedâncias associadas em série, que preservam a propriedade de autossimilaridade, generalizando o caso analisado na Ref. [49][49] C.X.M. dos Santos, C.M. Mendes e M.V. Freire, Revista Brasileira de Ensino de Física 40, e1302 (2018). para o caso de resistores puros. Consideremos uma impedância elementar para iniciar o processo. O processo iterativo começa com a adição de uma impedância reescalonada ao elemento original, e assim sucessivamente, tendo como fórmula recursiva a seguinte:
Abaixo mostramos o processo para os primeiros 4 passos:
Considerando que e levando o processo recursivo ao limite obtemos a série geométrica como fator de proporcionalidade, o que produz o resultado final:
Note que esse resultado pode ser obtido resolvendo a equação do ponto fixo [46[46] W.D. McComb, Renormalization Methods: A Guide For Beginners (Oxford University Press, USA, 2008).,49[49] C.X.M. dos Santos, C.M. Mendes e M.V. Freire, Revista Brasileira de Ensino de Física 40, e1302 (2018).]:
Vamos supor agora que queiramos medir a tensão sobre o elemento fazendo assim um divisor de tensão entre e . Para um divisor de tensão entre duas impedâncias associadas em série o valor da divisão , onde é a amplitude do estímulo, será dado simplesmente por . Nesse caso, para o circuito autossimilar considerado teremos:
uma vez que no ponto fixo. Observe que mesmo as impedâncias sendo dependentes da frequência, idealmente a divisão somente depende do fator de escala , sendo constante em frequência. Na prática, conforme já mencionado anteriormente para sistemas físicos reais, esse efeito é difícil de ser obtido pois não há como implementar o circuito autossimilar com complexidade infinita, ou seja, fazendo de fato.
4.2. O Circuito de Fração Continuada Autossimilar
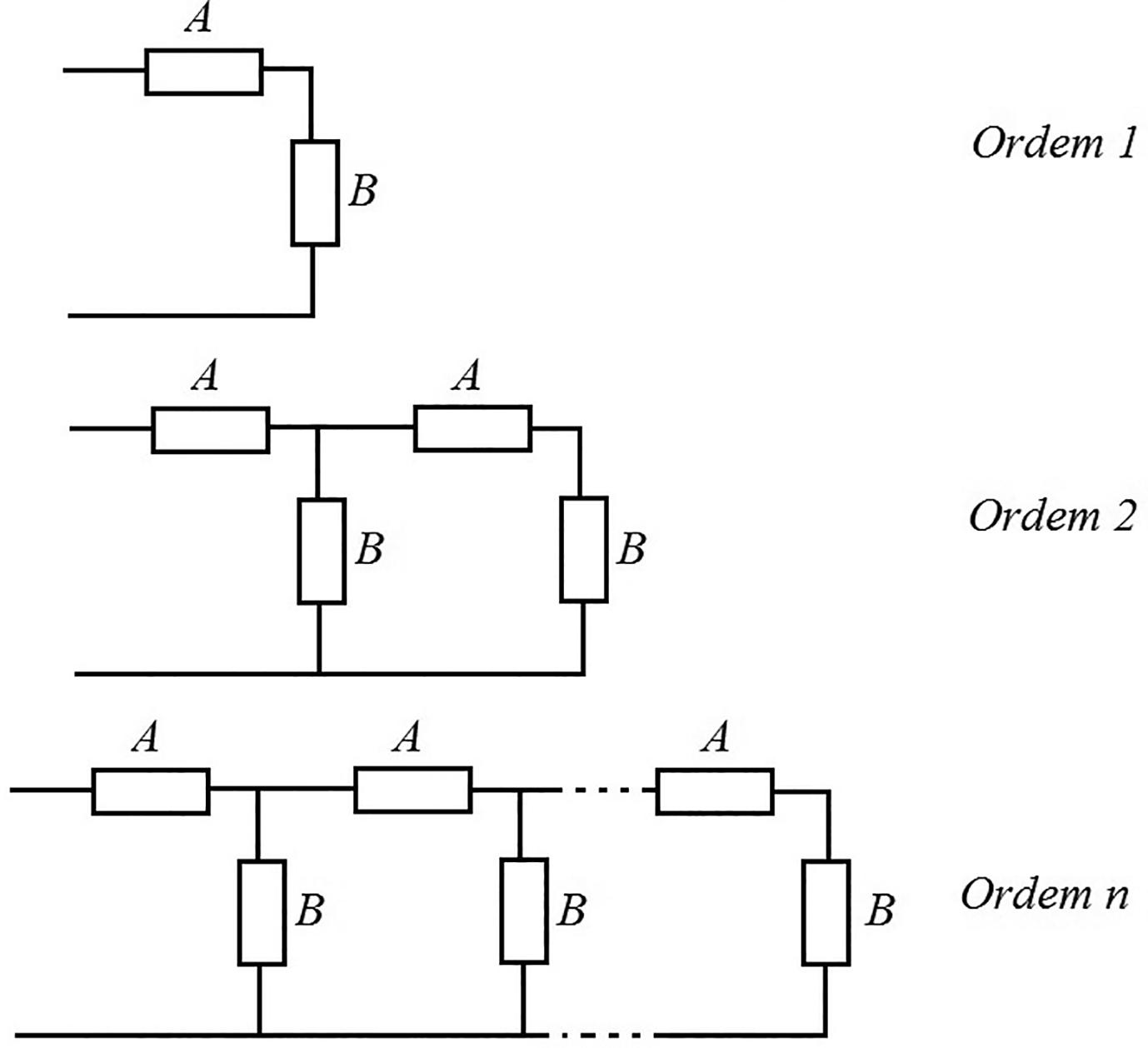
Considere agora o circuito ilustrado na Figura 7. Há dois tipos de impedâncias, denominadas de A e B, que são associadas em uma rede do tipo escada (ladder network).
A análise do circuito leva ao problema da expansão em frações continuadas. aqui vamos calcular a impedância no n-ésimo estágio associando ao circuito original um novo elemento idêntico , tal que a relação de recursão seja dada pela seguinte equação:
onde denota associação em paralelo dos elementos B e , e . A solução de ponto fixo, quando e é obtida da equação a seguir:
Há duas soluções possíveis:
Como podemos perceber, se é um resistor puro, a segunda solução produz um valor de resistência equivalente negativa, e somos forçados então a desconsiderar essa por razões físicas.
Queremos agora obter o divisor de tensão entre o elemento A e o seguinte que tem impedância , que tem valor igual ao do conjunto todo no ponto fixo:
Note que aqui a solução não é trivial como no caso da associação em série de impedâncias autossimilares e produz uma função de transferência dependente da escolha dos elementos, bem como da frequência. Um aspecto interessante é que a escolha de dois elementos imaginários puros de mesmo tipo para A e B produz uma resposta independente da frequência e de fase nula.
Agora vamos escolher como elementos um indutor e um capacitor . Nesse caso teremos:
Observe que com essa escolha o sistema autossimilar está representando uma linha de transmissão utilizando o consagrado modelo de elementos distribuídos, onde e , sendo e valores característicos de indutância por unidade de comprimento e capacitância por unidade de comprimento, respectivamente, e é o comprimento do segmento considerado na divisão da linha de comprimento total x em N partes de tamanho , é o comprimento de onda na frequência considerada. Teremos então:
Para valer o resultado de impedância de ponto fixo na descrição de uma linha de transmissão temos que fazer o número de segmentos , o que coloca o limite . Desse modo, o termo dominante será dado pela seguinte expressão:
onde claramente devemos adotar o sinal negativo (pois na raiz acima ) para obter um valor positivo para a chamada impedância característica da linha, ou seja, . O resultado final é , conforme o esperado para uma linha de transmissão ideal sem perdas [50[50] M.N.O. Sadiku, Elementos de Eletromagnetismo (Bookman Editora, Porto Alegre, 2012).,51[51] C. A. Dartora, A. Heilmann, F. Thomazi e E. Burkarter, Revista Brasileira de Ensino de Física 37, 1315 (2015).]. A função de transferência, que é o divisor de tensão entre dois pontos separados por uma distância , agora terá o seguinte valor:
onde utilizamos o fato de que é a velocidade de propagação de uma onda em uma linha de transmissão, é o número de onda ou constante de fase. O número complexo na forma pode ser colocado na forma polar (módulo e fase), sendo o módulo e a fase para um valor pequeno (o que deve ocorrer se ). Ese resultado é de fato esperado para uma linha de transmissão ideal, pois entre dois pontos a função de transferência é unitária, ocorrendo apenas um deslocamento de fase devido ao tempo de propagação do sinal para percorrer a distância . Veja que o atraso é dado por e o desvio de fase .
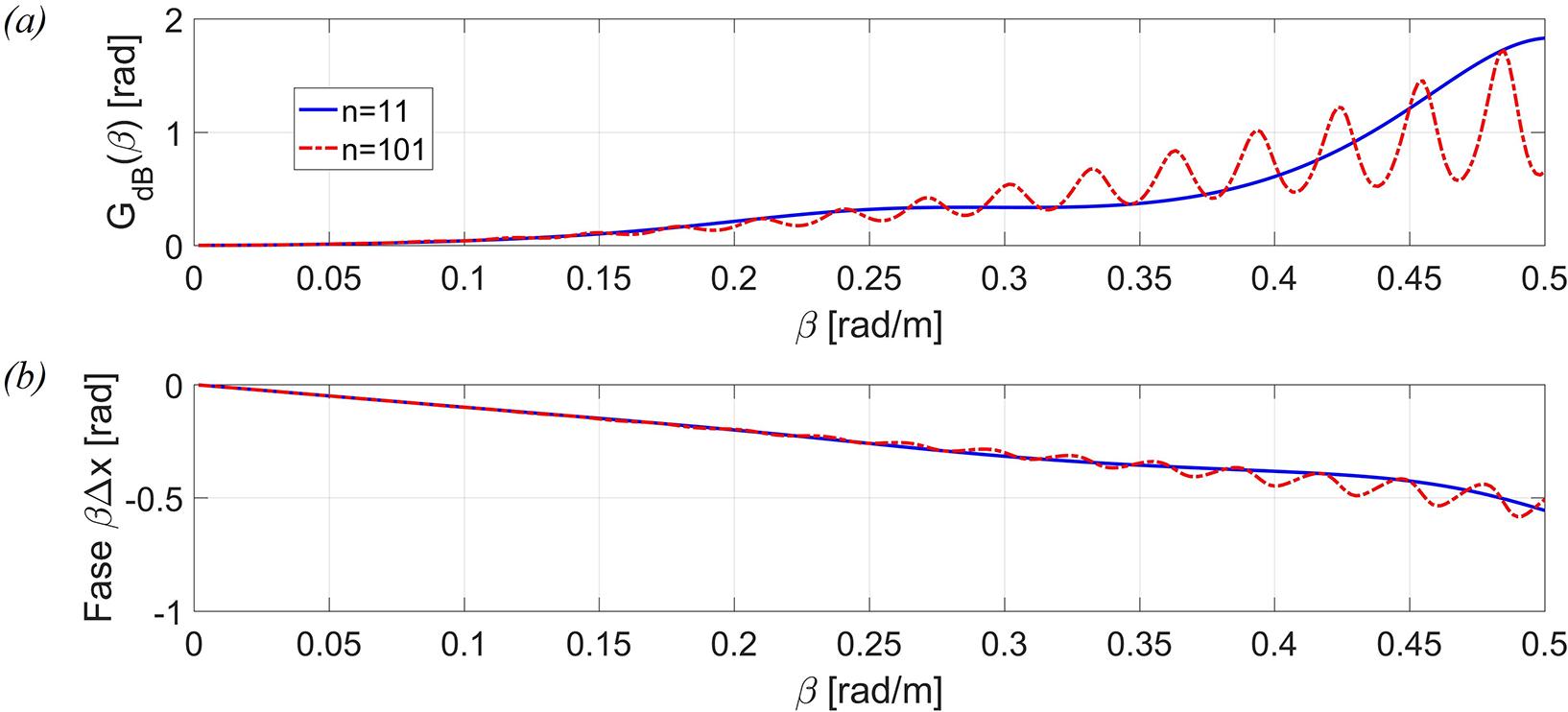
A Figura 8 ilustra o comportamento da função , calculada na forma completa (35), utilizando e . Foram utilizados e , por simplicidade, embora esses valores sejam muito diferentes da prática. A forma de magnitude em escala dB , e fase em radianos, em função de para dois valores distintos de é apresentada. A curva tracejada (azul) utiliza enquanto a curva cheia (vermelho) adota . Claramente o melhor resultado, corresponde ao esperado para uma linha de transmissão ideal, com magnitude 0dB para a transferência e fase variando de forma linear com ocorre para o valor menor de , o que é esperado, pois para que o modelo de parâmetros distribuídos seja efetivo é necessário que . Para os valores obtidos foram próximos do ideal para , a partir do qual a curva de fase perde a linearidade, enquanto que para , o resultado é aceitável para .
O comportamento da função , calculada na forma completa (35), utilizando e , com e . (a) magnitude em escala dB e (b) módulo da fase, em função de , para dois valores distintos de . A curva tracejada (azul) utiliza enquanto a curva cheia (vermelho) adota . Claramente o resultado, corresponde ao esperado para uma linha de transmissão ideal, com magnitude 0dB e o módulo da fase tendo comportamento linear, e tem mais aproximação com a idealidade quanto menor o valor de , o que é esperado.
Agora, uma estrutura escalonada por um fator de escala aplicado sobre a impedância produz a seguinte equação iterativa:
A equação para o ponto fixo continua quadrática e traz como solução os seguintes:
Aqui podemos fazer qualquer escolha de A e B, bem como de . No caso em que A e B sejam elementos puramente resistivos há duas situações distintas: i) então a solução (42) é a correta para o sistema, uma vez que e somente esta pode garantir a positividade requerida para o equivalente da associação de resistores; ii) e a solução (43) deve é obtida.
Para fins de análise, vamos considerar a normalização das impedâncias pelo valor de A, definindo e . Desse modo as equações podem ser reescritas na forma abaixo:
Um caso particular ocorre para e , em que a solução converge para dois possíveis pontos fixos . Claramente sendo A um valor real positivo, somente a solução positiva deve ser considerada, pois é o atrator para valores positivos de A e B. Portanto, uma associação em escada tem impedância equivalente convergindo para . A Figura 9 ilustra esse cenário através do gráfico de fluxo para distintos valores de impedância inicial z0, normalizada pelo valor de A.
Gráfico de fluxo para a função (44), com e . Note que a impedância normalizada rapidamente converge para , que funciona como atrator, ou ponto de equilíbrio estável dessa associação em escada. Os valores iniciais escolhidos foram e 4.
4.3. A linha de transmissão revisitada
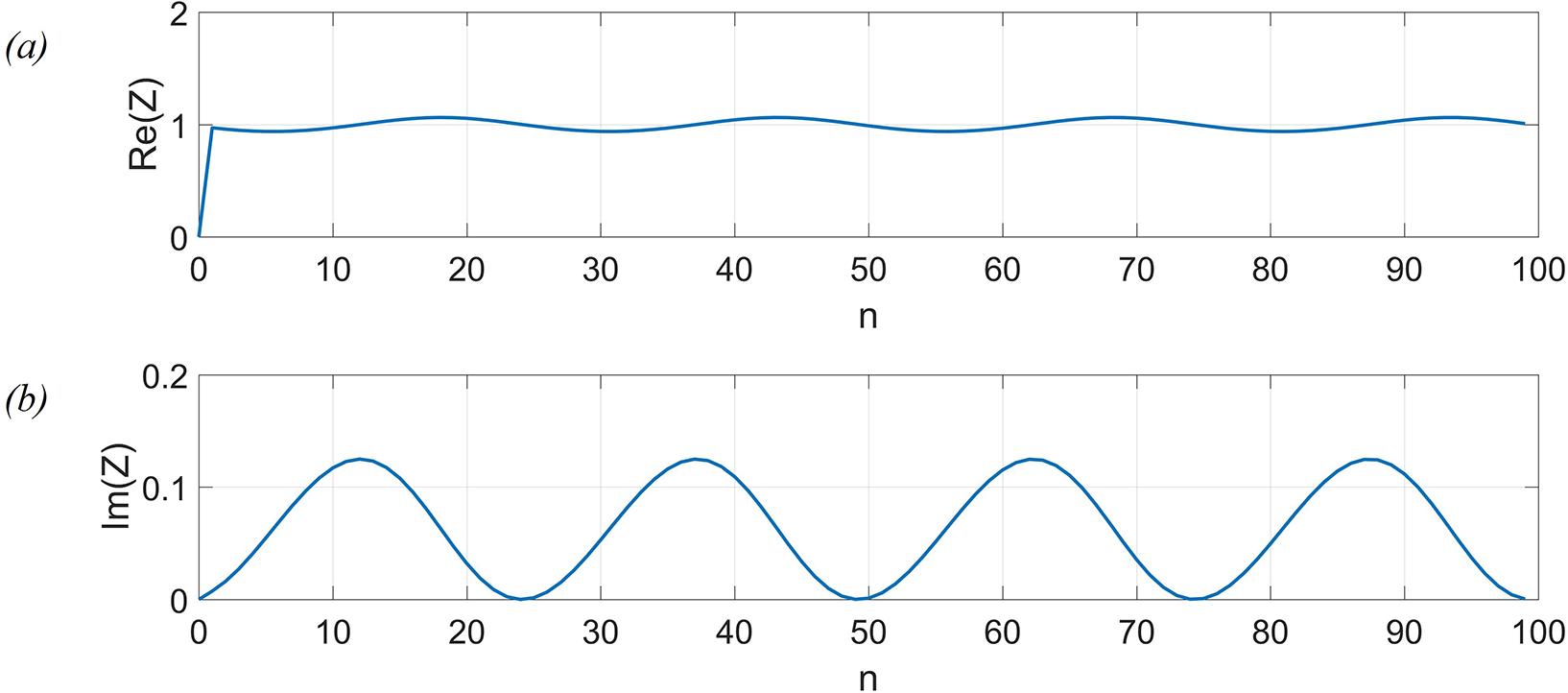
Consideremos agora o cálculo da função de transferência de uma linha de transmissão de forma recursiva. Sabemos para uma linha ideal infinita temos que fazer e , que é a chamada impedância característica da linha, é um número puramente real, mesmo que as impedâncias e sejam imaginários puros. Adotando esses valores para A e B o resultado para qualquer n finito de iterações não converge e torna-se oscilatório. Esse fato pode ser observado através da realização de uma planilha eletrônica de cálculo. Mas então como resolver esse problema numérico? A resposta aproximada passa pelo fato de que uma linha de transmissão infinita pode ser simulada por uma linha de transmissão de extensão finita com uma resistência de carga conectada aos seus terminais. Desse modo devemos fazer como condição inicial e então iniciar o processo iterativo, dado pela equação geral (41). A linha de transmissão convencional é obtida fazendo . A Figura 10 ilustra o processo iterativo de obtenção da impedância da linha com fazendo , e , para . A impedância de carga adicionada ao início do processo iterativo vale .
Gráfico de fluxo para (a) parte real e (b) parte imaginária da impedância de uma linha de transmissão convencional fazendo iterações, com , , e , para . A impedância de carga adicionada ao início do processo iterativo vale . Note que a parte real da impedância oscila em torno do ponto fixo . A parte imaginária também tem comportamento oscilatório e idealmente deve se anular, embora aqui oscile em torno do ponto médio de aproximadamente 0,06i.
Na Figura 11 é ilustrado o comportamento da função de transferência em magnitude(escala dB) e fase, obtidas a partir da forma recursiva abaixo
após n iteraçõe para a impedância, considerando . Observe que para valores a solução passa a divergir, o que é natural quando o modelo discreto da linha de transmissão (ou de parâmetros distribuidos) não mais satisfaz a condição . Enquanto a condição é satisfeita o modelo representa bem a função de transferência da linha. Os resultados foram obtidos para e iterações, para fins de comparação e nesse caso não se ganha melhores resultados simplesmente aumentando esse número. Para melhorar a resposta do modelo é necessário diminiuir o valor de , o que produz uma diminuição nos valore de L e C do modelo.
Gráfico da função de transferência (47), na forma de (a) magnitude, em escala dB, e (b) fase, considerando e iterações, , , , em função de , para . Após aproximadamente, a solução passa a divergir, independente do número de iterações, o que indica que a condição está sendo violada.
Consideramos ainda o caso de uma linha com fator de escalonamento , cujo gráfico de fluxo é ilustrado na Figura 12, fazendo iterações, o que já leva à convergência para o ponto fixo. Os demais parâmetros foram idênticos aos das Figuras 10 e 11, com , , e , para . A impedância de carga adicionada ao início do processo iterativo vale e no presente caso o ponto fixo converge para , tendo parte real nula.
Gráfico de fluxo para (a) parte real e (b) parte imaginária da impedância de uma linha de transmissão escalonada com , que converge já com iterações, com , , e , para . A impedância de carga adicionada ao início do processo iterativo vale . O ponto fixo vale , sendo a parte real nula.
Como comentário final vamos mencionar que vários elementos da engenharia eletromagnética, amplamente empregados no espectro das micro-ondas, por exemplo as antenas de aparelhos celulares, têm sido construídos utilizando os princípios da geometria fractal, sobretudo para otimizar a utilização do espaço disponível. Tipicamente, a impedância e a função resposta dessas estruturas não tem uma lei de escala com expoente igual ao da geometria fractal utilizada. Considerando-se uma antena dipolo elétrico utilizando um triângulo de Sierpinski, a dimensão fractal vale aproximadamente 1,586, mas a dimensão de escala da função de ganho dessa antena não é necessariamente na forma , onde é a frequência angular de referência (ou de projeto) e é a frequência de operação. O motivo pelo qual essas relações geralmente não se mantém é o fato de que ocorrem acoplamentos eletromagnéticos, surgimento de novas capacitâncias e indutâncias parasitas a cada iteração, e nesse caso, o comportamento eletromagnético é tipicamente obtido através de softwares e métodos numéricos de análise do problema.
5. Conclusões
Neste trabalho foi apresentada uma introdução à geometria fractal e ao conceito de invariância de escala e dos pontos fixos. Como exemplos, foram considerados a curva de Koch e o triângulo de Sierpinski para realizar de forma didática a determinação da dimensão de Hausdorff-Besicovitch. Na sequência foi apresentado o procedimento para a determinação de pontos fixos (ou também denominados pontos críticos). Esse é um problema essencial na teoria das transições de fase da matéria condensada, por exemplo, onde esses pontos correspondem a equilíbrios estáveis (pontos atratores) ou instáveis (repulsores), para os quais as flutuações facilmente retiram o sistema físico daquela condição. Além disso foi apresentado um breve panorama sobre a teoria da função de transferência, para ser aplicada, juntamente com a noção de invariância de escala e da determinação de pontos fixos ao problema da associação de impedâncias complexas, em duas configurações essenciais de circuitos que são a associação série e em escada. No caso da associação em série com complexidade infinita, o circuito apresenta uma função de transferência constante em frequência, mesmo para o caso em que os elementos de impedância utilizados sejam dependentes de . Isso pode ser interessante quando se faz necessária uma resposta plana em frequência. Todavia, na prática a complexidade infinita não pode ser realizada. O caso da associação em escada leva a uma expansão em frações continuadas e permitiu discutir o problema das linhas de transmissão e dos gráficos de fluxo para os pontos fixos de problemas de associação de impedâncias em escada. Conforme foi demonstrado aqui, a linha de transmissão ideal pode ser modelada a partir de uma associação em cascata autossimilar utilizando elementos indutivos e capacitivos.
Agradecimentos
C.A. Dartora agradece ao CNPq, pelo suporte financeiro parcial, através de Bolsas de Produtividade em Pesquisa CNPq 301848/2017-3. O presente trabalho foi realizado com apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Código de Financiamento 001.
Referências
-
[1]B.B. Mandelbrot, The Fractal Geometry of Nature (W. H. Freeman and Company, New York, 1982).
-
[2]B. Mandelbrot, Science 156, 636 (1967).
-
[3]G. Edgar, Measure, Topology, and Fractal Geometry (Springer Science & Business Media, Berlim, 2007).
-
[4]N. Gordon, Introducing fractal geometry (Icon Books, London, 2000).
-
[5]R.S. Strichartz, Differential equations on fractals: a tutorial (Princeton University Press, Nova Jersey, 2006).
-
[6]J.F. Gouyet, Physics and fractal structures (Masson Springer, New York, 1996).
-
[7]H. Takayasu, Fractals in the Physical Sciences (Manchester Univ. Press, Manchester, 1990).
-
[8]T. Nakayama, K. Yakubo and R. L. Orbach, Rev. Mod. Phys. 66, 381 (1994).
-
[9]A. Lesne e M. Laguës, Scale Invariance: From phase transitions to Turbulence (Springer-Verlag, Berlin, 2012).
-
[10]K.S. Miller e B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations (John Wiley & Sons, New York, 1993).
-
[11]K.B. Oldham e J. Spanier, The Fractional Calculus: Theory and Aplications, Differentiation and Integration to Arbitrary Order (Academic, New York, 1974).
-
[12]G.H. Hardy, Transactions of the American Mathematical Society 17, 301 (1916).
-
[13]B.R. Hunt, Proceedings of the American Mathematical Society 126, 791 (1998).
-
[14]T.A. de Assis, J.G.V. Miranda, F.B. Mota, R.F.S. Andrade e C.M.C. de Castilho, Revista Brasileira de Ensino de Física 30, 2304 (2008).
-
[15]H. Sagan, Space-Filling Curves (Springer-Verlag, New York, 1994).
-
[16]G. Julia, Journal de Mathématiques Pures et Appliquées 8, 47 (1918).
-
[17]P. Fatou, Comptes Rendus de l'Académie des Sciences de Paris 164, 806 (1917).
-
[18]T. Lei, Communications in Mathematical Physics 134, 587 (1990).
-
[19]F. Hausdorff, Mathematische Annalen 79, 157 (1919).
-
[20]A.S. Besicovitch, Mathematische Annalen 101, 161 (1929).
-
[21]A.S. Besicovitch e H.D. Ursell, Journal of the London Mathematical Society 12, 18 (1937).
-
[22]V. Zaburdaev, S. Denisov e J. Klafter, Rev. Mod. Phys. 87, 483 (2015).
-
[23]C. Vijayan e M. Ravikumar, J. Chem. Educ. 70, 830 (1993).
-
[24]S. Havlin e D. Ben-Avraham, J. Phys. A: Math. Gen. 15, L311 (1982).
-
[25]K. Tsujii, Polymer Journal 40, 785 (2008).
-
[26]J.P. Chen, S. Molchanov e A. Teplyaev, Journal of Physics A: Mathematical and Theoretical 48, 395203 (2015).
-
[27]E. Akkermans, G.V. Dunne e A. Teplyaev, Europhysics Letters 88, 40007 (2009).
-
[28]E. Akkermans, G.V. Dunne e A. Teplyaev, Phys. Rev. Lett. 105, 230407 (2010).
-
[29]S. Alexander e R. Orbach, Journal de Physique Lettres 43, 625 (1982).
-
[30]Y. Gefen, A. Aharony e S. Alexander, Phys. Rev. Lett. 50, 77 (1983).
-
[31]https://ieeexplore.ieee.org/abstract/document/6229091
» https://ieeexplore.ieee.org/abstract/document/6229091 -
[32]Y. Chen, PLoS ONE 6, e24791 (2011).
-
[33]M.K. Hassan e G.J. Rodgers, Physics Letters A 208, 95 (1995).
-
[34]J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford University Press, Reino Unido, 2002).
-
[35]F. Englert, J.M. Frère, M. Rooman e P. Spindel, Nuclear Physics B 280, 147 (1987).
-
[36]S.R. Best, IEEE Antennas and Wireless Propagation Letters 1, 74 (2002).
-
[37]S.R. Best, IEEE Antennas and Wireless Propagation Letters 2, 197 (2003).
-
[38]R. Hohlfeld e N. Cohen, Fractals 7, 79 (1999).
-
[39]J.P. Chen, L.G. Rogers, L. Anderson, U. Andrews, A. Brzoska, A. Coffey, H. Davis, L. Fisher, M. Hansalik, S. Loew e A. Teplyaev, J. Phys. A: Math. Theor. 50, 325202 (2017).
-
[40]P. Alonso-Ruiz, J. Math. Phys. 58, 073503 (2017).
-
[41]S.H. Yoon, European Journal of Physics 28, 277 (2007).
-
[42]B. Boyle, K. Cekala, D. Ferrone, N. Rifkin e A. Teplyaev, Pacific Journal of Mathematics 233, 15 (2007).
-
[43]C. Ucak, European Journal of Physics 30, 945 (2009).
-
[44]P. Jarry e J. Beneat, Design and Realizations of Miniaturized Fractal RF and Microwave Filters (Wiley, USA, 2009).
-
[45]https://bit.ly/2OqoDVE
» https://bit.ly/2OqoDVE -
[46]W.D. McComb, Renormalization Methods: A Guide For Beginners (Oxford University Press, USA, 2008).
-
[47]J. Zinn-Justin, Phase Transitions and Renormalization Group (Oxford University Press, USA, 2013).
-
[48]A.M.F. de Andrade, E.G. de Lima e C.A. Dartora, Revista Brasileira de Ensino de Fí-sica 40, e3314 (2018).
-
[49]C.X.M. dos Santos, C.M. Mendes e M.V. Freire, Revista Brasileira de Ensino de Física 40, e1302 (2018).
-
[50]M.N.O. Sadiku, Elementos de Eletromagnetismo (Bookman Editora, Porto Alegre, 2012).
-
[51]C. A. Dartora, A. Heilmann, F. Thomazi e E. Burkarter, Revista Brasileira de Ensino de Física 37, 1315 (2015).
Datas de Publicação
-
Publicação nesta coleção
10 Jan 2020 -
Data do Fascículo
2020
Histórico
-
Recebido
29 Jul 2019 -
Revisado
04 Nov 2019 -
Aceito
11 Nov 2019