Resumo
O oscilador harmônico amortecido por atrito de contato superficial é revisitado com uma descrição física e matemática mais robustas e abrangentes. Várias propriedades do sistema são apresentadas e discutidas, como a solução para o caso geral de condições iniciais, envoltórias do movimento, número exato de oscilações, dissipação instantânea e média de energia, fator de mérito, diagrama de fase dentre outras. Este texto serve como fundamentação teórica para simulações computacionais e experimentos didáticos que explorem sistemas oscilantes amortecidos por forças de atrito superficial.
Palavras-chave:
oscilador harmônico; osciladores amortecidos; atrito cinético
Abstract
The harmonic oscillator damped by frictional forces is revisited with a more robust and comprehensive physical and mathematical descriptions. Several system properties are presented and discussed, such as the solution to the general case of initial conditions, displacement envelopes, exact number of oscillations, instantaneous dissipation and average energy, quality factor, phase diagram and others. This text serves as a theoretical foundation for computer simulations and didactic experiments that explore oscillating systems damped by frictional forces.
Keywords:
harmonic oscillator; damped oscillators; kinetic friction
1. Introdução
O oscilador harmônico simples é talvez o mais célebre modelo na Física. Sua base matemática parte de um dos princípios mais fundamentais: o princípio de mínima energia. A importância do oscilador harmônico simples não é apenas para a fenomenologia Física, mas também para o próprio ensino de Física e Matemática, já que frequentemente serve de problema-padrão para aplicação de formulações físicas e técnicas matemáticas que vão sendo aprendidas nos cursos superiores como as mecânicas lagrangiana e hamiltoniana, solução da equação diferencial via coeficientes indeterminados, transformadas de Fourier e Laplace e assim por diante.
Como é apenas um modelo idealizado bastante simples, não raro faz-se adições de ingredientes físicos que tentam descrever mais adequadamente os fenômenos naturais, como forças produzidas por agentes externos e dissipativos de energia. O segundo é muito comum de se encontrar em livros didáticos de Mecânica Clássica em uma única forma: amortecimento produzido por uma força de arrasto dinâmica oposta à velocidade da partícula [1[1] S.T. Thornton e J.B. Marion, Dinâmica clássica de partículas e sistemas (Cengage Learning, São Paulo, 2011)., 2[2] W. Greiner, Classical mechanics: systems of particles and hamiltonian dynamics (Springer, New York, 2003).]. Há algumas décadas, Hickmann e Libardi [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997). e Marchewka, Abbott e Beichner [4][4] A. Marchewka, D.S. Abbott e R.J. Beichner, Am. J. Phys. 72, 4 (2004). fizeram estudos acerca de um oscilador harmônico simples amortecido por força de atrito de contato, típica de problemas simples de cinemática. Hickmann e Libardi [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997). denominaram esse sistema como oscilador linearmente amortecido, nomenclatura que será adotada aqui. Contudo, ambos os estudos anteriores tiveram uma descrição bastante limitada do sistema, pois detiveram-se apenas em condições iniciais com velocidade nula, não apresentaram propriedades importantes do sistema como equações das envoltórias do movimento, quantidade de oscilações, classificação dos tipos de amortecimento, balanço energético do sistema etc. Neste trabalho são apresentadas essas e várias outras propriedades para condições iniciais generalizadas, de modo que o oscilador linearmente amortecido fica completamente caracterizado, servindo de referencial teórico para simulações ou experimentos que possam ser elaborados visando esse sistema. Para simplificar a descrição matemática, o oscilador encontra-se na horizontal.
As duas próximas seções servirão para modelar matematicamente a força de atrito, formulando uma expressão geral a partir da descrição fenomenológica, bem como a equação de movimento do oscilador linearmente amortecido. A quarta seção está dedicada a apresentar as soluções da equação de movimento do oscilador linearmente amortecido bem como as propriedades desse sistema, listadas anteriormente. Finalizando essa seção, é apresentado um comparativo entre o oscilador linearmente amortecido e o oscilador harmônico amortecido. No fim, tem-se as conclusões gerais do trabalho.
2. Força de atrito
Sabe-se que a força de atrito depende fundamentalmente do estado de movimento do corpo, da rugosidade da superfície (avaliada pelos coeficientes de atrito estático e cinético e , respectivamente) e da força normal de apoio que essa superfície exerce sobre o corpo [5[5] D. Halliday, R. Resnick e J. Walker, Fundamentos de Física (LTC, Rio de janeiro, 2016), v. 1, 9ª ed., 6[6] H.M. Nussenzveig, Curso de Física Básica (Edgard Blücher, São Paulo, 2002), v. 1, 4ª ed.]. Quando o corpo está em repouso, a força de atrito iguala-se à força externa resultante. Aumentando-se a força aplicada, eventualmente o corpo entra em movimento. Na iminência de sair do repouso, a força de atrito assume seu valor máximo dado pela conhecida expressão , onde a orientação (dada pelo sinal) está sempre oposta à da força externa. Já em movimento, a força de atrito assume um valor sempre constante , onde o sinal dá-se de forma a opor-se à velocidade do corpo. Esse valor da força de atrito é independente do valor da força aplicada ou da velocidade do corpo. Em geral, [5[5] D. Halliday, R. Resnick e J. Walker, Fundamentos de Física (LTC, Rio de janeiro, 2016), v. 1, 9ª ed., 6[6] H.M. Nussenzveig, Curso de Física Básica (Edgard Blücher, São Paulo, 2002), v. 1, 4ª ed.], o que significa fisicamente que é mais difícil retirar um corpo do repouso do que mantê-lo em movimento. A Figura 1 ilustra essa discussão.
Evolução da força de atrito com diferentes forças aplicadas. Na situação (a) a força externa não é suficiente para retirar o corpo do repouso porque a força de atrito possui a mesma intensidade e direção oposta, e isso permanece até que o módulo da força de atrito assuma o valor . Na situação (b) a força aplicada é maior que a força de atrito, que nesse caso assume o valor . Na situação (c) tem-se uma força aplicada maior que a mostrada na situação (b), mas a força de atrito permanece a mesma.
Em símbolos, a força de atrito possui uma série de expressões matemáticas, dependendo da situação física em questão (repouso ou movimento). No caso do oscilador harmônico, a força aplicada é aquela produzida pela mola , onde ω é a frequência (angular) de oscilação natural do sistema massa-mola. Quando a massa está em movimento, a força de atrito é constante e dada pela expressão acima citada [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997).. Quando a massa está em repouso (pontos de retorno da trajetória, incluindo eventualmente a condição inicial), a força de atrito dependerá do valor da força restauradora da mola. Para a força de atrito não consegue equilibrar a força restauradora e o movimento acontece. Entretanto, quando a força de atrito equilibra exatamente a força harmônica e o movimento cessa. Assim, após atingir um ponto de retorno, a massa volta a mover-se ou permanece em repouso dependendo se o valor de . Dessa forma, a região pode ser chamada zona de parada, pois se a partícula tiver velocidade nula dentro dessa região, o movimento acaba. Colecionando todas essas possibilidades, a força de atrito f em um sistema massa-mola pode ser escrita como:
As condições para são usadas apenas para os pontos de retorno ou para a parada final, ou seja, em instantes específicos de tempo. As duas primeiras condições são as únicas que podem ser usadas na equação de movimento, já que são definidas em um intervalo de tempo, e não em um instante.
3. Equações de movimento
Para simplificar a descrição do fenômeno, vou assumir uma notação semelhante à usada por Hickmann e Libardi [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997). e associar cada etapa do movimento do oscilador com um número inteiro n. Por construção, n = 0 indexa das condições iniciais até a primeira parada, n = 1 até a segunda parada, n = 2 até a terceira parada e assim por diante. A Figura 2 mostra um esquema de como essa notação funciona para esse tipo de oscilador.
Esboço do movimento de um oscilador linearmente amortecido (linha cheia). O índice n indexa cada trecho do movimento que inicia em e finaliza em , onde é o ponto de retorno. Após um determinado número de oscilações a massa para.
Usando essa notação indexada, a força de atrito mostrada na Equação (1) pode ser reescrita como uma só expressão usando a função sinal e o delta de Kronecker da seguinte maneira:
onde
em que
são a função sinal e delta de Kronecker, respectivamente. Note que é definido apenas com as condições iniciais. Assim, com essa expressão para a força de atrito, a equação de movimento fica também indexada por n:
onde em analogia a definido anteriormente e os tempos e indicam o domínio temporal da equação, ou seja, os tempos onde acontecem os pontos de retorno ou a parada completa.
4. Resultados
4.1. Soluções para o oscilador
A solução geral da Equação (4) é dada pela soma das soluções geral e particular:
Note que as constantes a e b foram também indexadas, ou seja, cada semi-oscilação possui uma solução. Para conhecer completamente essas expressões de , devemos determinar todos os , e . Vamos começar determinando os tempos .
Sabendo que o n-ésimo trecho do movimento é definido entre e , todas as velocidades avaliadas em com são nulas (não necessariamente a velocidade é nula em por causa das condições iniciais), ou seja
e a substituição da derivada de (5) na expressão acima resulta em
Devido à periodicidade da função tangente em e juntamente com a imposição física de para qualquer n, a equação anterior fornece
Usando o princípio da indução, podemos determinar todos os em função de :
e então
sendo determinado usando a expressão (6)
Para determinar os e , vamos partir do princípio que posição e velocidade são quantidades sempre contínuas em qualquer instante de tempo, em particular no tempo
onde ambas as condições em (9) valem para . Ao substituir a solução geral (5) e sua derivada primeira em (9), encontramos o seguinte sistema de equações:
que, com a ajuda de (7), resultam em
Podemos trabalhar nas expressões recursivas de e da Equação (10) da mesma maneira que fizemos para , colocando dessa vez e como referência, onde estes devem ser determinados pelas condições iniciais. Assim
e o processo indutivo nos leva às seguintes expressões para e :
e para encontrar a dependência explícita de e com os parâmetros iniciais de posição e velocidade, precisamos conhecer e a partir das condições iniciais e . Como por construção as condições iniciais pertencem ao segmento n = 0:
o que leva ao resultado
e a substituição direta de e nas Equações (11) leva a conhecer os parâmetros e na forma
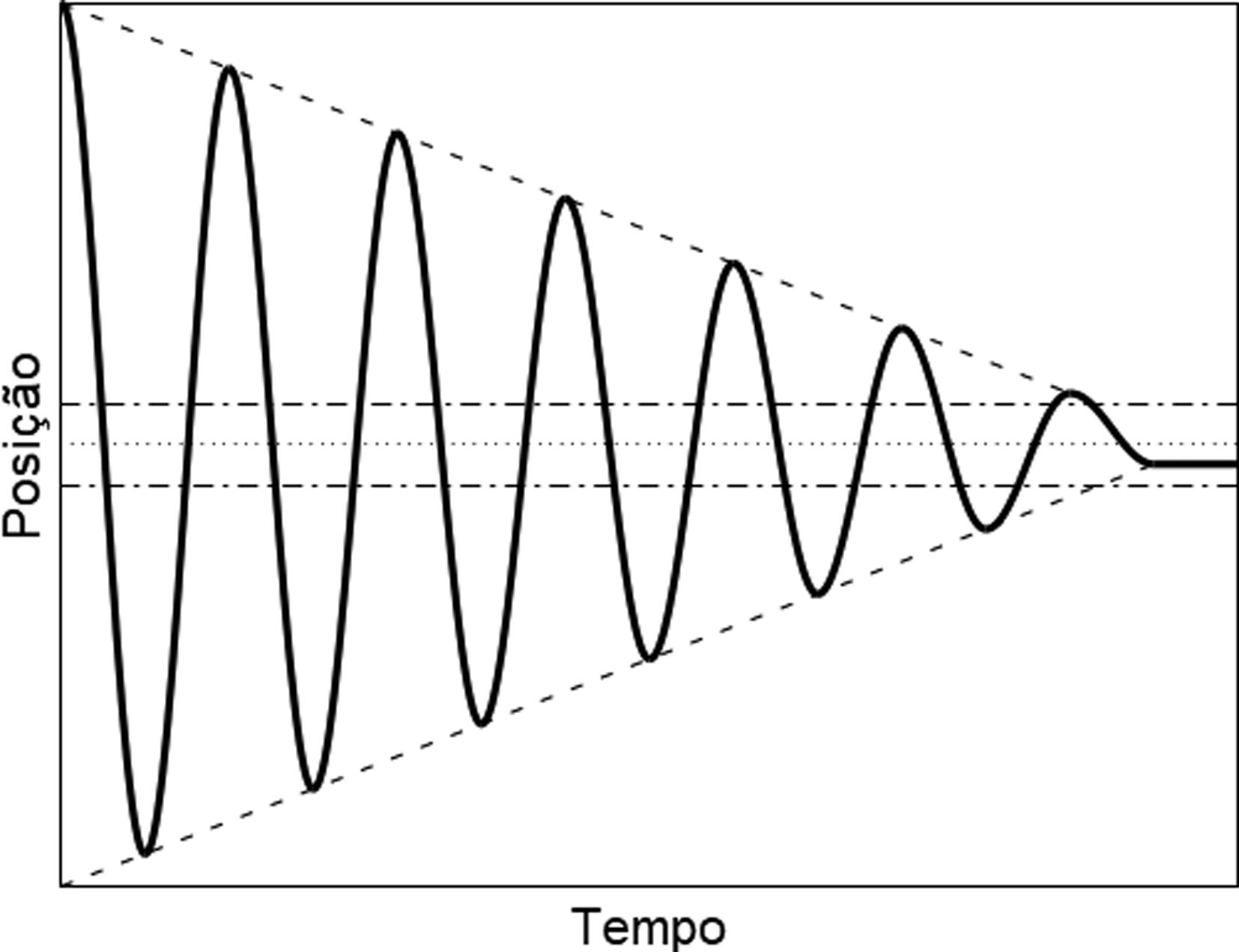
Assim, a solução final do oscilador linearmente amortecido e os instantes onde acontecem as paradas ficam conhecidos completamente em função dos parâmetros definidos pelas condições iniciais graças às Equações (13) e (7) e também em função do tempo dado em (8). A Figura 3 mostra, esquematicamente, como é a função horária da posição do oscilador linearmente amortecido.
Esquema da função horária da posição para o oscilador linearmente amortecido (linha cheia). As retas tracejadas são as envoltórias do movimento e as linhas horizontais (ponto e traço) são os limites da zona de parada na qual a força de atrito não equilibra a força harmônica da mola, isto é, dentro desses limites o movimento não acontece.
As derivadas primeira (velocidade) e segunda (aceleração) da posição do oscilador são mostradas na Figura 4.
Esquema da velocidade (esquerda) e aceleração (direita) para o oscilador linearmente amortecido em correspondência à Figura 3.
Uma observação importante: a aceleração do oscilador harmônico linearmente amortecido não é contínua, como mostra a Figura 4. Isso é consequência da descontinuidade da força de atrito (1) nos instantes de retorno do movimento. O valor da descontinuidade na aceleração nesses pontos pode ser calculada facilmente, e vale
que é constante e independente de n ou da condição inicial.
4.2. Número de trechos
É possível determinar exatamente em que trecho e posição o oscilador harmônico linearmente amortecido irá parar. A condição física para isso é dada na quinta expressão da força de atrito (1) que estabelece o encerramento do movimento. A condição matemática de parada em n = N do oscilador linearmente amortecido é escrita como
Fazendo a substituição das equações (11) e (7) com n = N na expressão acima, resulta em
Podemos multiplicar os dois lados da desigualdade por que o sentido da desigualdade não se inverte. Assim, é possível chegar ao seguinte par de inequações:
Dessas duas expressões, apenas a primeira guarda realidade física com o fenômeno estudado. O menor valor inteiro de N que satisfaz a condição de parada é, portanto, dado por
em que a função ceiling(arg) retorna o mínimo inteiro maior ou igual ao argumento (função teto).
4.3. Envoltórias do movimento
Podemos encontrar as expressões para as envoltórias do movimento do oscilador linearmente amortecido. Sabemos que essas envoltórias são linhas retas que conectam os máximos (envoltória superior) ou os mínimos (envoltória inferior) do movimento [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997).. De maneira geral, podemos encontrar a equação da reta que conecta dois extremos similares por meio da expressão
que, após alguma álgebra simples usando as Equações (5), (7) e (11), chegamos ao resultado
onde o sinal surgiu porque a expressão dentro dos colchetes é multiplicada por . As envoltórias do movimento são mostradas na Figura 3 pelas linhas tracejadas.
4.4. Tipos de amortecimento
É possível estabelecer categorias de amortecimento semelhantes ao oscilador harmônico amortecido convencional. A análise completa para condições iniciais genéricas é muito complicada, por isso, apenas nesta subseção, adotaremos um caso especial de condições iniciais onde a partícula é solta no lado positivo de x. Matematicamente:
Essas condições fornecem pela equação (3) e quando aplicadas nas equações (8) e (12) produzem
A categorização dos amortecimentos será dada em termos de , que marca a posição da primeira parada após o movimento iniciar, ou seja, o tipo de amortecimento é dado em termos da partícula fazer a primeira parada e retornar ou não. Usando as expressões anteriores para , e na equação (5), a posição da primeira parada fica dada por
e usando essa expressão para avaliar todas as posições possíveis de , tem-se:
em que na primeira expressão a partícula atravessa toda a zona de parada, que significa um retorno; na segunda a partícula para após a posição de equilíbrio e antes do fim da zona de parada; na terceira a partícula para exatamente na posição de equilíbrio e na quarta expressão a partícula para sem passar pela posição de equilíbrio. Todas devem obedecer à condição adicional para que haja movimento. Essa condição aplicada no conjunto anterior produz a restrição para que o movimento possa ocorrer nas duas últimas expressões além de alterar o limite inferior de no último caso para cumprir a condição física . Assim, podemos resumir as categorias de amortecimento de acordo com a Tabela 1.
Esses tipos de amortecimento são mostrados esquematicamente na Figura 5.
As terminologias foram escolhidas para guardar analogia com o oscilador harmônico amortecido. O tipo “subcrítico” ainda consegue executar pelo menos uma oscilação. O termo “crítico” foi escolhido para a (única) condição que leva a partícula a finalizar o movimento na posição de equilíbrio sem oscilar. O tipo “supercrítico” divide-se em dois casos: irrestrito, no qual a partícula passa pela posição de equilíbrio e para, não sendo necessária uma relação entre os coeficientes de atrito para que esse caso aconteça e o restrito, em que a partícula para antes de chegar na posição de equilíbrio, que só existe se os coeficientes de atrito obedecerem à relação . Todos esses tipos de amortecimento são mostrados na Tabela 1. Nota-se que não é possível encontrar uma posição onde a partícula pode ser solta e não entrar na zona de parada ou mesmo interromper o movimento exatamente no início da zona de parada, em , ou seja, para qualquer condição inicial e , a força restauradora trará sempre a partícula para dentro da zona de parada.
Sobre as relações entre os coeficientes de atrito, é importante destacar que para sistemas cujos coeficientes de atrito sejam tais que , as condições crítica e supercrítica restrita deixam de existir. Isso significa que é obrigatório para a partícula passar pela posição de equilíbrio antes de parar. Em particular, sem a condição crítica de amortecimento, é impossível encontrar uma posição para soltar a partícula e esta parar exatamente na posição de equilíbrio sem realizar pelo menos uma oscilação.
Assim, diferentemente do que afirmaram Hickmann e Libardi [3][3] J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997)., é possível estabelecer tipos de amortecimento para o oscilador linearmente amortecido, onde esses tipos estão relacionados com condições intrínsecas do problema (restrições aos valores dos coeficientes de atrito), em analogia ao oscilador harmônico amortecido (relações entre a frequência natural de oscilação e o parâmetro de amortecimento) e também com variáveis extrínsecas ao sistema: a posição inicial do oscilador. Uma análise completamente generalizada dos tipos de amortecimento pode até ser possível, porém resultaria em expressões demasiadamente complicadas que destoariam da simplicidade do fenômeno. Assim, as condições aqui postas para os tipos de amortecimento são suficientemente gerais para caracterizar o oscilador linearmente amortecido nesse aspecto.
4.5. Energia, potência e diagrama de fase do oscilador linearmente amortecido
A energia mecânica do oscilador, composta das partes cinética e potencial harmônica, também será indexada de acordo com cada trecho do movimento amortecido
resultando, após a substituição da equação (5) e sua derivada primeira em
Entretanto, esse valor instantâneo da energia não é muito interessante para fins práticos, já que oscila com o tempo. A média temporal é mais útil, sendo definida, no caso do oscilador harmônico linearmente amortecido, entre dois instantes de retorno consecutivos:
sendo que o cálculo da média temporal das funções harmônicas que aparecem em (16) resulta em
e ao serem substituídas em (17) considerando as expressões em (16) e (11) produzem
Para se criar uma expressão para a energia média que dependa do tempo, vamos fazer o seguinte artifício: tomaremos o tempo no meio do intervalo entre dois instantes de retorno consecutivos, ou seja,
e fazendo esse procedimento na última expressão para a energia média por trecho encontramos diretamente
que tem uma dependência quadrática no tempo. A Figura 6 mostra esquematicamente as energias instantânea e média para o oscilador harmônico linearmente amortecido. Nota-se claramente que a energia instantânea oscila em torno do valor médio como definido aqui, o que é melhor observado pela miniatura na Figura 6.
Energias instantânea (linha cheia) e média (linha tracejada) para o oscilador linearmente amortecido. A miniatura mostra uma parte do gráfico maior, onde pode-se ver melhor a oscilação da energia instantânea em torno do valor médio.
Os instantes de retorno do movimento são identificados, no gráfico , pelos pontos de inflexão da curva, como mostrado na miniatura da Figura 6.
A potência do oscilador linearmente amortecido pode ser calculada derivando-se a energia em função do tempo:
que também fica indexado para cada trecho. Após substituir na definição acima a derivada da equação (5) e a força de atrito dada em (2), encontra-se a potência instantânea
que também oscila no tempo, tendo o valor médio como função do tempo um significado mais prático, assim como a energia. Para obter pode-se fazer um procedimento análogo na expressão acima ao que foi feito para a energia ou simplesmente derivar a expressão (18) em relação a t:
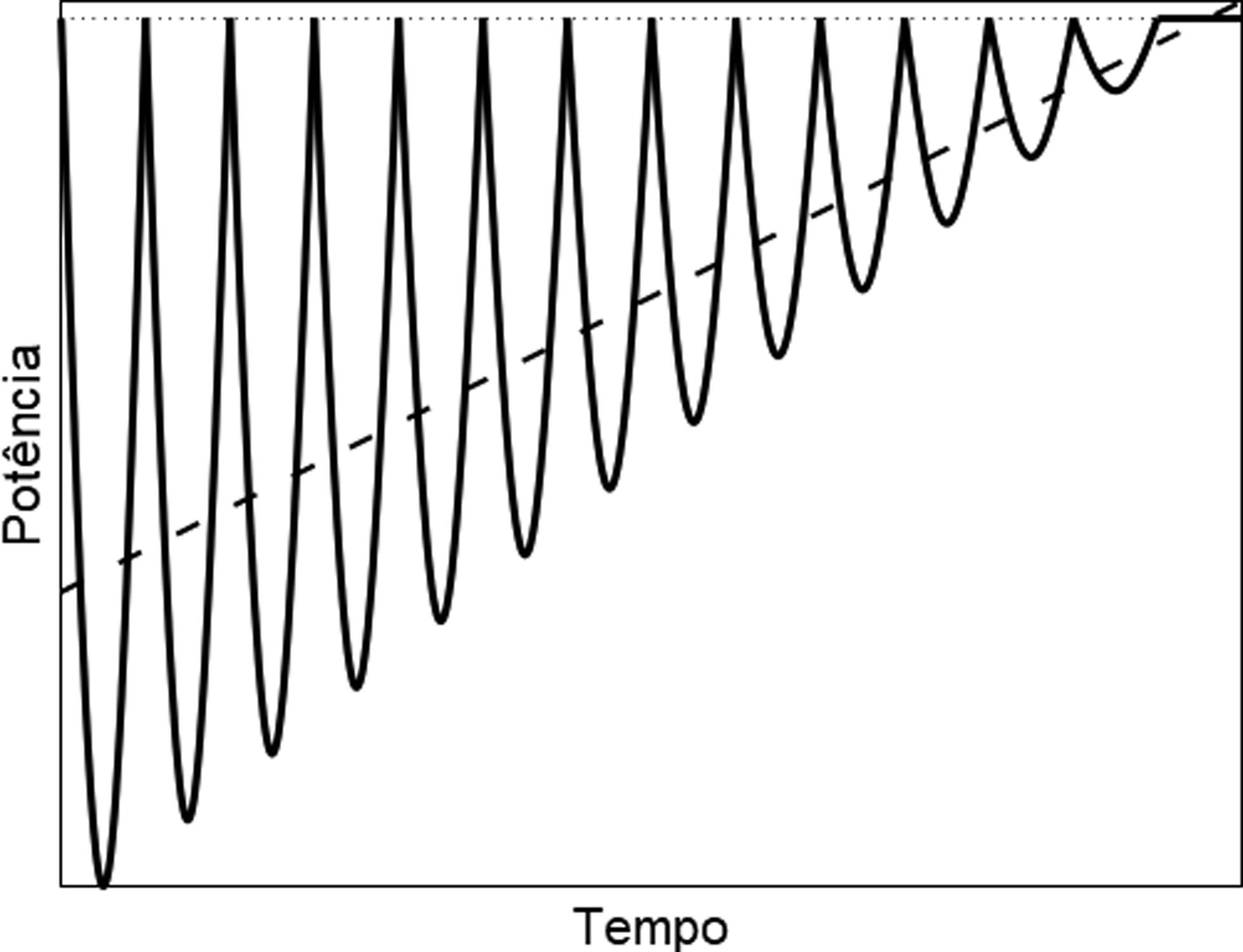
e, evidentemente, a potência média tem uma dependência linear com o tempo. A Figura 7 mostra o esquema para as potências instantânea e média do oscilador linearmente amortecido.
Potências instantânea (linha cheia) e média (linha tracejada) para o oscilador linearmente amortecido.
Como na energia instantânea os instantes de retorno são indicados pelos pontos de inflexão da função , a potência irá anular-se nesses instantes. Isso já era esperado pois como a potência dissipada é o produto da velocidade pela força de atrito, quando a velocidade é nula, a potência também é, porque a força de atrito nunca é zero.
Também pode-se determinar o fator de mérito Q do oscilador linearmente amortecido, cuja definição geral é [7][7] H.M. Nussenzveig, Curso de Física Básica (Edgard Blücher, São Paulo, 2002), v. 2, 4ª ed.
A energia dissipada por ciclo para o oscilador linearmente amortecido é dada por
que, quando substituída na definição do fator de mérito (20) tem-se
que não será colocada explicitamente por ser uma expressão racional entre um polinômio do segundo grau (energia) e um do primeiro (potência) em t. A função fator de mérito do oscilador linearmente amortecido é mostrada esquematicamente na Figura 8.
Fator de mérito do oscilador linearmente amortecido. A função só é definida até o instante , pois a partir desse tempo a potência dissipada é constantemente nula.
Para o oscilador linearmente amortecido o fator de mérito é função praticamente linear do tempo e diminui seu valor até atingir o mínimo no instante que o movimento acaba. Isso significa que o sistema responde de maneira diferente ao amortecimento à medida que o tempo passa, o que difere substancialmente do oscilador harmônico amortecido, cujo fator de mérito é constante.
Por fim, o diagrama de fase, que é o gráfico paramétrico de do oscilador linearmente amortecido é mostrado esquematicamente na Figura 9.
O diagrama de fase exibe um comportamento espiral, onde cada passo da espira está linearmente espaçado um do outro, consequência direta do tipo de amortecimento constante que sofre esse oscilador. A trajetória da partícula no diagrama de fase se dá a partir do ponto mais externo , que são as condições iniciais, e segue sobre a espiral no sentido horário até chegar no ponto que marca o fim do movimento. Cada trecho n do oscilador linearmente amortecido é um arco de elipse localizado acima ou abaixo do eixo horizontal.
4.6. Comparação com o oscilador harmônico amortecido
Exploradas várias propriedades e parâmetros do oscilador linearmente amortecido, é salutar exibir uma comparação com os resultados análogos ao conhecido oscilador harmônico amortecido. As comparações são resumidas na Tabela 2.
Comparações entre as principais características do oscilador linearmente amortecido e o oscilador harmônico amortecido tradicional.
É possível notar a riqueza de fenômenos associados ao oscilador linearmente amortecido. Desde a necessidade de se separar o movimento em trechos, cada um obedecendo a uma equação diferencial, passando pela maior gama de situações de amortecimento, em comparação com o oscilador harmônico amortecido, onde, a depender da relação entre os coeficientes de atrito, alguns tipos de amortecimento são proibidos, criando uma espécie de regra de seleção para esse fenômeno até a análise energética, em que o principal destaque é, devido às diferentes dependências temporais da energia e potência médias, o fator de mérito do oscilador linearmente amortecido não é constante, mas uma função praticamente linear do tempo, que diminui até um valor mínimo dado no instante de parada final do movimento do sistema.
5. Conclusões
O oscilador linearmente amortecido foi revisitado, desta vez com mais detalhes e fornecendo uma descrição matemática generalizada. A indexação dos trechos do movimento foi uma consequência da particularidade da força de atrito e tal indexação se manteve em praticamente todos os observáveis físicos do sistema. Foi possível determinar várias propriedades importantes para o estudo do movimento, como o número exato de oscilações que o sistema executa, os tipos de amortecimento, as envoltórias do movimento, energia e potência médias.
Esse oscilador, por ser amortecido por forças de atrito, torna-se experimentalmente mais simples que o oscilador harmônico amortecido dos livros de Física do Ensino Superior, cuja força dissipativa depende da velocidade. Assim, o sistema estudado neste trabalho está mais próximo da realidade de experimentações simples realizadas em laboratórios didáticos. Toda a fundamentação teórica necessária para a compreensão e explicação do fenômeno foi exposta aqui.
Referências
-
[1]S.T. Thornton e J.B. Marion, Dinâmica clássica de partículas e sistemas (Cengage Learning, São Paulo, 2011).
-
[2]W. Greiner, Classical mechanics: systems of particles and hamiltonian dynamics (Springer, New York, 2003).
-
[3]J.S. Hickmann e H. Libardi, Rev. Bras. Ens. Fis. 19, 3 (1997).
-
[4]A. Marchewka, D.S. Abbott e R.J. Beichner, Am. J. Phys. 72, 4 (2004).
-
[5]D. Halliday, R. Resnick e J. Walker, Fundamentos de Física (LTC, Rio de janeiro, 2016), v. 1, 9ª ed.
-
[6]H.M. Nussenzveig, Curso de Física Básica (Edgard Blücher, São Paulo, 2002), v. 1, 4ª ed.
-
[7]H.M. Nussenzveig, Curso de Física Básica (Edgard Blücher, São Paulo, 2002), v. 2, 4ª ed.
Datas de Publicação
-
Publicação nesta coleção
28 Out 2019 -
Data do Fascículo
2020
Histórico
-
Recebido
05 Ago 2019 -
Revisado
25 Ago 2019 -
Aceito
26 Ago 2019