Abstract
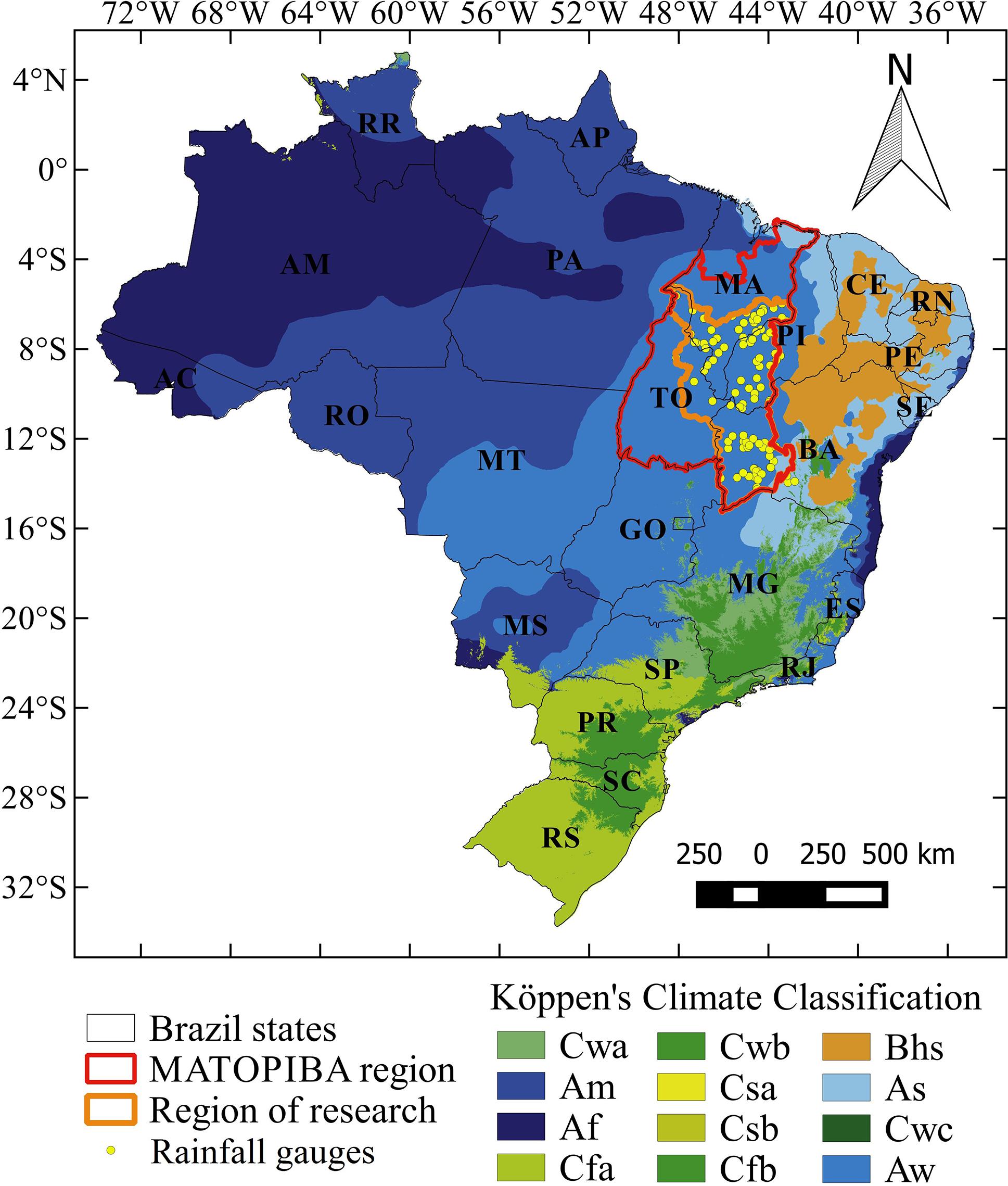
The region of study was MATOPIBA, located in the north of Brazilian Savanna biome (Cerrado), encompassing part of north/northeast of Brazil. The region has been gaining prominence in the last years due to the expansion of agricultural over this area. The aims of this study were: to adjust parameters for rainfall intensity-duration-frequency; and to identify the most vulnerable agricultural areas to erosion based on erosivity and erodibility. The rainfall intensity-duration-frequency function were adjusted using series of maximum annual rainfall event from 105 rainfall gauges. Gumbel model was the most efficient to simulate the maximum rainfall intensity, where these data were used to adjusted the rainfall intensity-duration-frequency model based on K, a, b and c parameters. The most rainfall gauges showed intensity between 51 and 80 mm h-1 and 81 and 120 mm h-1, respectively, for return period of 2 and 100 years with rainfall duration of 30 minutes. The higher rainfall intensity was observed mainly in the central-north of the region associated with rainfall systems. The rainfall intensity showed a huge capacity to cause soil erosion based on the erosivity energy, while the moderate erodibility was observed for areas with Ferralsols and Leptosols and low erodibility for areas with Arenosols.
Keywords:
Gumbel model; return years; soil erosion; erosivity; erodibility; Brazilian Savanna
Resumo
A região de estudo foi o MATOPIBA, localizado no norte do Cerrado Brasileiro. Esta região vem ganhando destaque pela expansão de área agrícolas nos últimos anos. Desta forma, o objetivo deste estudo foi ajustar parâmetros para estimativa da intensidade-duração-frequência de chuva, e identificar áreas agrícolas com maior risco de erosão baseado nos índices de erosividade e erodibilidade. As funções de intensidade-duração-frequência de chuva foram ajustadas usando series de valor máximo de chuva de 105 estações pluviométricas. O modelo Gumbel foi o que melhor simulou a distribuição de máxima intensidade de chuva, usada para ajustar os coeficientes K, a, b e c da relação intensidade-duração-frequência. A maioria das estações obteve intensidades entre 51 e 80 mm h-1, e 81 e 120 mm h-1, respectivamente, para período de retorno de 2 e 100 anos com duração de 30 minutos. As maiores intensidades foram observadas na região central-norte, que está associada ao sistemas de chuvas. A intensidade de chuva mostrou-se capaz de causar elevado risco de erosão, considerando a energia de erosividade. Enquanto que erodibilidade apresentou moderado risco para latossolos e neossolos litólicos, e baixo para neossolos quartzarênicos.
Palavras-chave:
modelo Gumbel; anos de retorno; erosão do solo; erosividade; erodibilidade; cerrado
Introduction
The MATOPIBA is a region located in the north of Brazilian Savanna biome (Cerrado), comprising the most of Maranhão (MA) and Tocantins (TO) states, and the Southwest of Piauí (PI) and West of Bahia (BA) states. The region has been gaining prominence in the recent years due to the expansion of agricultural over this area. The MATOPIBA represented 9.28% of grain production in Brazil, with a total area of over 7 million hectares (MAPA, 2017MAPA - MINISTéRIO DA AGRICULTURA, PECUáRIA E ABASTECIMENTO. Projeções do Agronegócio no Brasil - 2016/17 a 2026/27. MAPA. Brasília, 86 pp, 2017.). The main crops grown are soybean, cotton, maize and rice (CONAB, 2018CONAB. Survey of Crop Season. Available at: [http://www.conab.gov. br/conteudos.php?a=1253&]. Accessed on: [January, 2018].
http://www.conab.gov. br/conteudos.php?a...
).
The climate was classified as Aw (tropical zone with dry winter) in the most of area, following the Köppen climate classification (Alvares et al., 2013ALVARES C.A.; STAPE J.L.; SENTELHAS P.C.; GONçALVES J.L.M.; SPAROVEK G. Köppen’s climate classification map for Brazil. Meteorologische Zeitschirift, v. 22, p. 711-728, 2013.). The rainfall is concentrated from October to April, totalizing between 1000 and 1600 mm year-1 (INMET, 2017INMET. Clima - Normais Climátologicas do Brasil. Available at: [http://www.inmet.gov.br/portal/index.php?r=clima/normaisClimatologicas]. Accessed on: [November, 2017].
http://www.inmet.gov.br/portal/index.php...
). The higher rainfall quantity falling in a short period increase the risk of erosion in agricultural areas (Wu et al., 2017WU, Z.; WEI, Y.; WANG, J.; XIA, J.; CAI, C. et al. Effects of erosion degree and rainfall intensity on erosion processes for Ultisols derived from quaternary red clay. Agriculture, Ecosystems and Environment, v. 249, p. 226-236, 2017.) and water losses (Wang et al., 2015WANG, H.; GAO, J.E.; ZHANG, M-J.; LI, X-H.; ZHANG, S-L. et al. Effects of rainfall intensity on groundwater recharge based on simulated rainfall experiments and a ground flow model. Catena, v. 127, p. 80-91, 2015.). The risk of erosion and water losses can be reduced with a better plan of hydraulic works in the agriculture.
Hydraulic works in agriculture include erosion control, dump spillways, drainage systems and stormwater galleries (Damé et al., 2012DAMé, R.C.F.; TEIXEIRA, C.F.A.; GONçALVES, T.; SANTOS J.P.S.; QUADRO, M.S. Erosividade sob duas durações de intensidades máximas da chuva em Pelotas - RS. Revista Agroambiental On-line, v. 6, p. 1-8, 2012.). The efficiency of these systems goes through a good planning based on temporal and spatial rainfall intensity-duration-frequency. The intensity-duration-frequency relationships are used to characterize the maximum rainfall patterns (Oliveira et al., 2005OLIVEIRA, L.F.C.; CORTêS, F.C.; WEHR, T.R.; BORGES, L.B.; SARMENTO, P.H.L. Intensidade-duração-frequência de chuvas intensas para localidades o Estado de Goiás e Distrito Federal. Pesquisa Agropecuária Tropical, v. 35, p. 13-18, 2005.), which is essential to dimension the size of the structure in agriculture to reduce erosion and water losses.
The soil characteristics are other important point for analyze the risk of erosion and water losses. The Universal Soil Loss Equation was developed based on five factors, being: erosivity, erodibility, slope steepness and length, land use and cropping management, and control erosion practices (Nearing et al., 2017NEARING, M.A.; YIN, S-Q.; BORRELLI, P.; POLYAKOV, V.O. Rainfall erosivity: An historical review. Catena, v. 157, p. 357-362, 2017.). Erosivity represents the maximum energy of rainfall per unit of rainfall depth, related with maximum rainfall intensity in 30 minutes (Zheng and Chen, 2015ZHENG, M.G.; CHEN, X. Statistical determination of rainfall-runoff erosivity indices for single storms in the Chinese loess plateau. Plos One, v. 10, n. 3, e0117989, 2015.), while erodibility represent the soil erosion susceptibility in function of soil texture and structure, organic matter content and soil permeability (Jones et al., 1996JONES, D.S.; KOWALSKI, D.; SHAW, R.B. Calculating revised universal soil loss equations (RUSLE) estimates on Departament of Defense Lands: A review of Rusle factors and US Army Land Conditions- trend analysis (LCTA) data gaps. Departament of Forest Science, Colorado State University, Fort Collins, 9 p. 1996.).
This way, the aims of this study were: 1) to adjusted parameters for intensity-duration-frequency relationship from daily rainfall disaggregation; 2) to determine the maximum rainfall intensity in 30 minutes for return period of 2, 5, 10, 25, 50 and 100 years; and 3) to analyses the most vulnerable agricultural areas to erosion based on erosivity and erodibility in the region of MATOPIBA, Brazil.
2.Material and Methods
2.1.Study area
The region of study were the main agricultural areas in the MATOPIBA, including the South of Maranhão (MA) state, the Northeast of Tocantins (TO) state, the Central-South of Piauí (PI) state, and West of Bahia (BA) state in Brazil (Fig. 1). The climate was classified as a tropical zone with dry winter (Aw) for the most of the area, and tropical zone with dry summer (As) for a small region in the Southeast, following the Köppen climate classification (Alvares et al., 2013ALVARES C.A.; STAPE J.L.; SENTELHAS P.C.; GONçALVES J.L.M.; SPAROVEK G. Köppen’s climate classification map for Brazil. Meteorologische Zeitschirift, v. 22, p. 711-728, 2013.). Annual rainfall range between 1000 and 1600 mm year-1, occurring mostly between October and April (INMET, 2017INMET. Clima - Normais Climátologicas do Brasil. Available at: [http://www.inmet.gov.br/portal/index.php?r=clima/normaisClimatologicas]. Accessed on: [November, 2017].
http://www.inmet.gov.br/portal/index.php...
).
Köppen’s climate classification, location of rainfall gauges, and delimitation of MATOPIBA and research region. Adapted from Alvares et al. (2013).
Rainfall data
Rainfall data were obtained from the National Hydrometeorological Network of the National Water Agency (ANA, 2014ANA - AGêNCIA NACIONAL DE áGUAS. Hidroweb. Available at: [http://www.snirh.gov.br/hidroweb]. Accessed on: [April, 2014].
http://www.snirh.gov.br/hidroweb...
) for 105 gauges located in 35 cities. The period of daily record rainfall ranged from 15 to 65 years along the sites. A consistency analysis was done to eliminate rainfall gauges with less than 15 years of records and with missing data. The 15 years of records is a minimum data considered by MAPA (2018)MAPA - MINISTéRIO DA AGRICULTURA, PECUáRIA E ABASTECIMENTO. Zoneamento Agrícola. Available at: [http://www.agricultura.gov.br/assuntos/riscos-seguro/risco-agropecuario/portarias]. Accessed on: [August, 2018].
http://www.agricultura.gov.br/assuntos/r...
for agricultural zoning, which defined the adaptability of a region for agricultural purposes. The rainfall series showed to be stationarity, which was verify by linear regression and the level of significance. In each hydrological year was selected the higher rainfall event occurred in one day to build the series of probability distribution for the maximum rainfall intensity, which make each maximum event independent.
Rainfall disaggregation
The maximum rainfall intensity was estimated based on the relationship between the total rainfall and the period. The maximum rainfall intensity was disaggregated from a daily period to 1440 minutes, from 1440 min to 720, 600, 480, 360 and 60 minutes, from 60 minutes to 30, and from 30 minutes to 25, 20, 15, 10 and 5 minutes. The rainfall disaggregation was done by multiplying the reference value for a proportion coefficient adjusted in DAAE-CESTESB (1980)DAEE/CETESB - DEPARTAMENTO DE áGUA E ENERGIA ELéTRICA / COMPANHIA DE TECNOLOGIA DE SANEAMENTO AMBIENTAL. Drenagem urbana: Manual de projeto. DAEE-CETESB, São Paulo, 466 pp, 1980., which was used by different authors for the Cerrado biome (Oliveira et al. 2005OLIVEIRA, L.F.C.; CORTêS, F.C.; WEHR, T.R.; BORGES, L.B.; SARMENTO, P.H.L. Intensidade-duração-frequência de chuvas intensas para localidades o Estado de Goiás e Distrito Federal. Pesquisa Agropecuária Tropical, v. 35, p. 13-18, 2005.; 2008OLIVEIRA, L.F.C.; ANTONINI, J.C.A.; FLOREZE, A.P.; SILVA, M.A.S. Métodos de estimativa de precipitação máxima para o Estado de Goiás. Revista Brasileira de engenharia Agrícola e Ambiental, v. 12, p. 620-625, 2008.; Campos et al., 2014CAMPOS, A.R.; SANTOS, G.G.; SILVA, J.B.L.; IRENE FILHO, J.; LOURA, D.S. Equações de intensidade-duração-frequência de chuvas para o estado do Piauí. Revista Ciência Agronômica, v. 45, p. 488-498, 2014.). The use of general parameters was did due to the rainfall data were obtained daily and there was no data available for the region at a smaller frequency to generate an appropriated rainfall disaggregation for the regional condition, as recommended by Koutsoyiannis et al. (1998)KOUTSOYIANNIS, D.; KOZONIS, D.; MANETAS, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. Journal of Hydrology, v. 206, p. 118-135, 1998..
2.4.Modelling intensity-frequency-duration (IFD) curves
The maximum rainfall intensity was submitted to the statistical analysis to adjust the best probabilistic model, considering different rainfall duration (1440, 720, 600, 480, 360, 60, 30, 25, 20, 15, 10 and 5 minutes). Gumbel, Log-Normal with 2 and 3 parameters, Pearson and Log-Pearson III were the models tested for the maximum rainfall intensity in the pre-analysis. The Gumbel model showed the best performance between the tested models based on chi-square test.
After obtained the Gumbel parameters for maximum rainfall intensity and duration, the inverse of Gumbel was used to calculate the maximum rainfall intensity for different duration and return period, as present in Eq. (1).
where: i j (mm h-1) is the maximum rainfall intensity for the duration period of 1440, 720, 600, 480, 360, 60, 30, 25, 20, 15, 10 and 5 minutes, and return periods of 2, 5, 10, 25, 50 and 100 years; imean (mm h-1) and var are, respectively, the mean and the variance of maximum annual rainfall intensity for the entire series records in the rainfall gauge for each duration period and return periods; and Rp (years) is the return period.
The IFD curves were adjusted based on the simulated series of probability distribution based on inverse of Gumbel model for the maximum rainfall intensity, considering rainfall duration of 1440, 720, 600, 480, 360, 60, 30, 25, 20, 15, 10 and 5 minutes, and return periods of 2, 5, 10, 25, 50 and 100 years, using Eq. (2). The K, a, b and c parameters were adjusted for the IFD probabilistic model using the minimum squares method.
where: imaxS (mm h-1) is the maximum rainfall intensity simulated (mm h-1); Rp is the return period (years); t is the period of rainfall duration (minutes), and K, a, b and c are adjusted parameters for each rainfall gauge.
The results for IFD curves were compared against observed maximum rainfall intensity to analyze their performance. The statistical indexes used to analyze the model performance were: mean absolute error (MAE), root mean square error (RMSE), determination coefficient (r²) and Willmott coefficient (d).
2.5.Erosion risk analysis
Erosivity and erodibility indexes were used to identify the most vulnerable agricultural areas to erosion and water losses, based on the Universal Soil Loss Equation (Nearing et al., 2017NEARING, M.A.; YIN, S-Q.; BORRELLI, P.; POLYAKOV, V.O. Rainfall erosivity: An historical review. Catena, v. 157, p. 357-362, 2017.). The erosivity was quantified based on the maximum 30 minutes rainfall intensity, using the Gumbel model with parameters adjusted for each rainfall gauge for the return period of 2, 5, 10, 25, 50 and 100 years. The maximum rainfall 30 minutes intensity was used due to better correlation with soil losses for a single rainfall event (Wischmeier et al., 1958WISCHMEIER, W.H.; SMITH, D.D.; UHLAND, R.E. Evaluation of factors in the soil-loss equation. Agricultural Engineering, v. 39, p. 458-462, 1958.; Zheng and Chen, 2015ZHENG, M.G.; CHEN, X. Statistical determination of rainfall-runoff erosivity indices for single storms in the Chinese loess plateau. Plos One, v. 10, n. 3, e0117989, 2015.). The erodibility value was obtained based on the soil type (IBGE, 2012IBGE. Interactive Maps: Soils. Available at: [http://mapas.ibge.gov.br]. Accessed on: [February, 2012].
http://mapas.ibge.gov.br...
) and the soil texture (RADAM, 1974RADAM. Levantamento de recursos naturais. Departamento Nacional da Produção Mineral (DNPM), Rio de Janeiro, 374 pp, 1974.), following Wanielista (1978)WANIELISTA, M.P. Stormwater management: Quality and quantity. Ann Harbor Science Publishers, Michigan, 383 pp, 1978., and the risk level, following Jones et al. (1996)JONES, D.S.; KOWALSKI, D.; SHAW, R.B. Calculating revised universal soil loss equations (RUSLE) estimates on Departament of Defense Lands: A review of Rusle factors and US Army Land Conditions- trend analysis (LCTA) data gaps. Departament of Forest Science, Colorado State University, Fort Collins, 9 p. 1996.. The others parameters of Universal Soil Loss Equation were not included in the analysis due to limitation of information to compute the risk of erosion.
Results and Discussions
3.1.IFD curves model
The maximum rainfall intensity distribution was adjusted using the Gumbel probabilistic model, which had the best fit between pre-tested models. Gumbel probabilistic model is the most widely used for rainfall intensity-duration-frequency relationship (Koutsoyiannis et al., 1998KOUTSOYIANNIS, D.; KOZONIS, D.; MANETAS, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. Journal of Hydrology, v. 206, p. 118-135, 1998.; Beskow et al., 2015BESKOW, S.; CALDEIRA, T.L.; MELLO, C.R. DE; FARIA, L.C.; GUEDES, H.A.S. Multiparameter probability distributions for heavy rainfall modeling in extreme southern Brazil. Journal of Hydrology: Regional Studies, v. 4, p. 123-133, 2015.). The model was used to describe the maximum rainfall distribution in different sites around world, as in Saudi Arabia (Elsebaie, 2012ELSEBAIE, I.H. Developing rainfall intensity-duration-frequency relationship for two regions in Saudi Arabia. Journal of King Sand University - Engineering Sciences, v. 24, p. 131-140, 2012.), Israel (Ben-Zvi, 2009BEN-ZVI, A. Rainfall intensity-duration-frequency relationships derived from large partial duration series. Journal of Hydrology, v. 367, p. 104-114, 2009.) and south of Brazil (Cardoso et al., 2014CARDOSO, C.O.; BERTOL, I.; SOCCOL, O.J.; SAMPAIO, C.A.P. Generation of intensity duration frequency curves and intensity temporal variability pattern of intense rainfall for Lages/SC. Brazilian Archives of Biology and Technology, v. 57, p. 274-283, 2014.).
The IFD model had r² and d coefficients above 0.9798, with the highest mean absolute error (MAE) and root mean square error (RMSE), respectively, of 8.15 mm h-1 and 10.41 mm h-1 in the site of Barreiras (Data not showed), which was the longest rainfall gauge records (65 years), when compared observed and simulated values. The model efficiency was kept in Colinas, which had only 15 years of full rainfall records (Data not showed). In this site, the r² and d coefficients were above 0.9830, with the highest MAE and RMSE, respectively, of 8.77 mm h-1 and 11.19 mm h-1. The good fit also was observed for the other rainfall gauges used in the study (Data not showed).
3.2.IFD model parameters
The IFD model was adjusted based on the K, a, b and c parameters for the rainfall gauges to estimate rainfall intensity in different return periods and rainfall duration. The K, a, b, and c parameters were adjusted for each rainfall gauge in the states of Tocantins (Table 1), Maranhão (Table 2), Piauí (Table 3) and Bahia (Table 4). The b and c were parameters stable between the analyzed sites, where b ranged between 9.760 and 10.514, and c between 0.725 and 0.745. The parameters b and c lead a reduction of rainfall intensity when theirs values were higher.
Parameters values obtained for estimate rainfall intensity-frequency-duration curves for cities in Piauí state
Parameters values obtained for estimate rainfall intensity-frequency-duration curves for cities in Bahia state
The K and a parameters had higher variation between the rainfall gauges (Table 1, 2, 3 and 4), where higher values for these parameters increased rainfall intensity. The K parameter ranged between 552 and 1169, occurring, respectively, in the rainfall gauge of Matina, Bahia state (Table 4), and Vereda Grande, Maranhão state (Table 2). The parameter a varied between 0.10, for the rainfall gauge of Ibipira, Maranhão state (Table 2) and São Sebastião do Tocantinas, Tocantins state (Table 1), and 0.26, in Eliseu Martins, Piauí state (Table 3).
Parameters values obtained for estimate rainfall intensity-frequency-duration curves for cities in Tocantins state
Parameters values obtained for estimate rainfall intensity-frequency-duration curves for cities in Maranhão state
Rainfall intensity
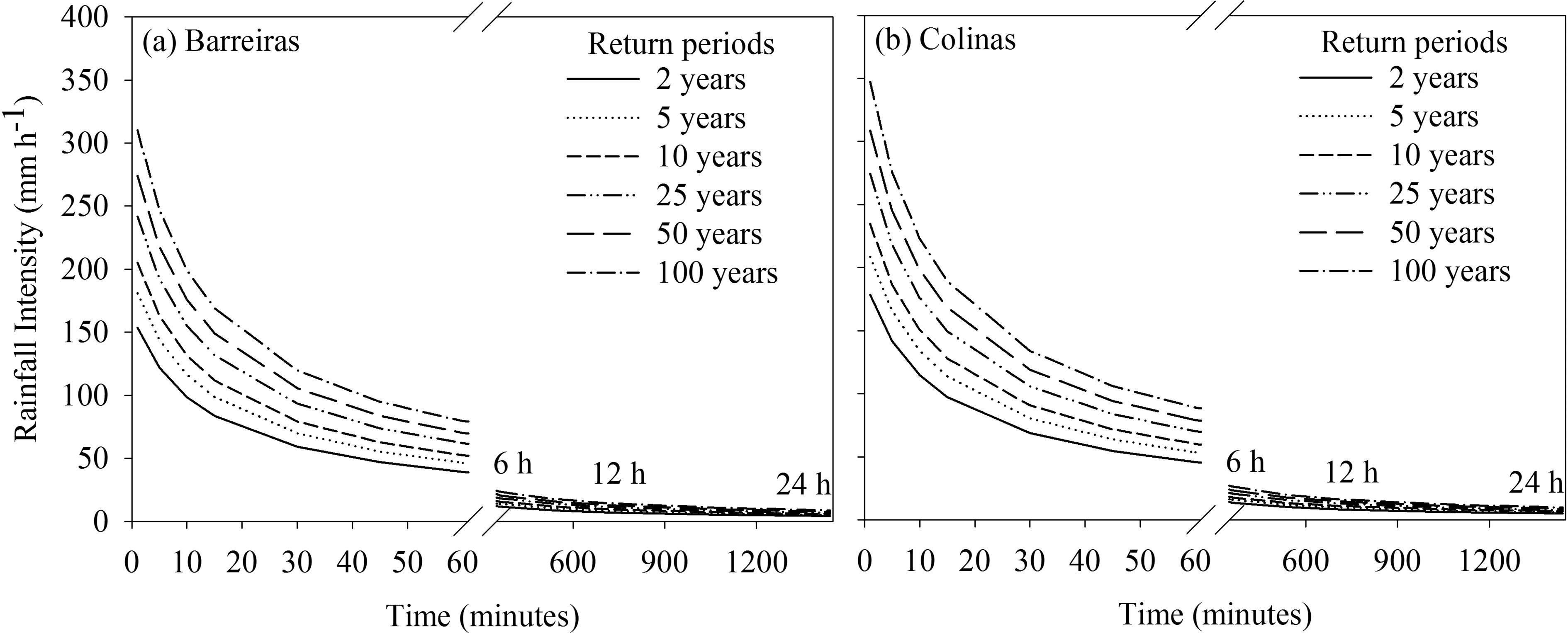
The sites of Barreiras and Colinas were used as a case of study, due to be the longest and shortest rainfall records, respectively, of 65 and 15 years. The rainfall intensity was 59 and 120 mm h-1 in 30 minutes in Barreiras, respectively, for return period of 2 and 100 years (Fig. 2a). In Colinas, the rainfall intensity was higher, being 69 and 134 mm h-1 in 30 minutes, respectively, for return period of 2 and 100 years. In the south of Brazil, Cardozo et al. (2014)CARDOSO, C.O.; BERTOL, I.; SOCCOL, O.J.; SAMPAIO, C.A.P. Generation of intensity duration frequency curves and intensity temporal variability pattern of intense rainfall for Lages/SC. Brazilian Archives of Biology and Technology, v. 57, p. 274-283, 2014. observed lower maximum rainfall intensity, being of 47 mm h-1 in 30 minutes for return period of 2 years. Longer return periods increased rainfall intensity (Figs. 2-3), as observed by other authors (Elsebaie, 2012ELSEBAIE, I.H. Developing rainfall intensity-duration-frequency relationship for two regions in Saudi Arabia. Journal of King Sand University - Engineering Sciences, v. 24, p. 131-140, 2012.; Cardoso et al., 2014CARDOSO, C.O.; BERTOL, I.; SOCCOL, O.J.; SAMPAIO, C.A.P. Generation of intensity duration frequency curves and intensity temporal variability pattern of intense rainfall for Lages/SC. Brazilian Archives of Biology and Technology, v. 57, p. 274-283, 2014.; Tfwala et al., 2017TFWALA, C.M.; VAN RENSBURG, L.D.; SCHALL, R.; MOSIA, S.M.; DLAMINI, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Climate Risk Management, v. 16, p. 1-9, 2017.).
Simulated rainfall intensity for return periods of 2 (a), 5 (b), 10 (c), 25 (d), 50 (e) and 100 (f) years and raining period between 1 and 1440 minutes by Gumbel model in Barreiras (a) and Colinas (b).
Rainfall intensity was 310 and 347 mm h-1, respectively, for Barreiras and Colinas, for a rainfall of 1 minute and return period of 100 years (Fig. 2). Otherwise, rainfall intensity dropped to 9 and 10 mm h-1, respectively, for Barreiras and Colinas, when the rainfall had a duration of 24 hours. The reduction of rainfall intensity with longer raining period is an expected tendency, but the intensity was related with local climate (Elsebaie, 2012ELSEBAIE, I.H. Developing rainfall intensity-duration-frequency relationship for two regions in Saudi Arabia. Journal of King Sand University - Engineering Sciences, v. 24, p. 131-140, 2012.; Cardoso et al., 2014CARDOSO, C.O.; BERTOL, I.; SOCCOL, O.J.; SAMPAIO, C.A.P. Generation of intensity duration frequency curves and intensity temporal variability pattern of intense rainfall for Lages/SC. Brazilian Archives of Biology and Technology, v. 57, p. 274-283, 2014.; Tfwala et al., 2017TFWALA, C.M.; VAN RENSBURG, L.D.; SCHALL, R.; MOSIA, S.M.; DLAMINI, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Climate Risk Management, v. 16, p. 1-9, 2017.). For example, Elsebaie et al. (2012)ELSEBAIE, I.H. Developing rainfall intensity-duration-frequency relationship for two regions in Saudi Arabia. Journal of King Sand University - Engineering Sciences, v. 24, p. 131-140, 2012. observed maximum rainfall intensity reducing from 38 mm h-1 in 10 minutes, to 1.74 mm h-1 in 24 hours, for return period of two years in Najran region, Saudi Arabia.
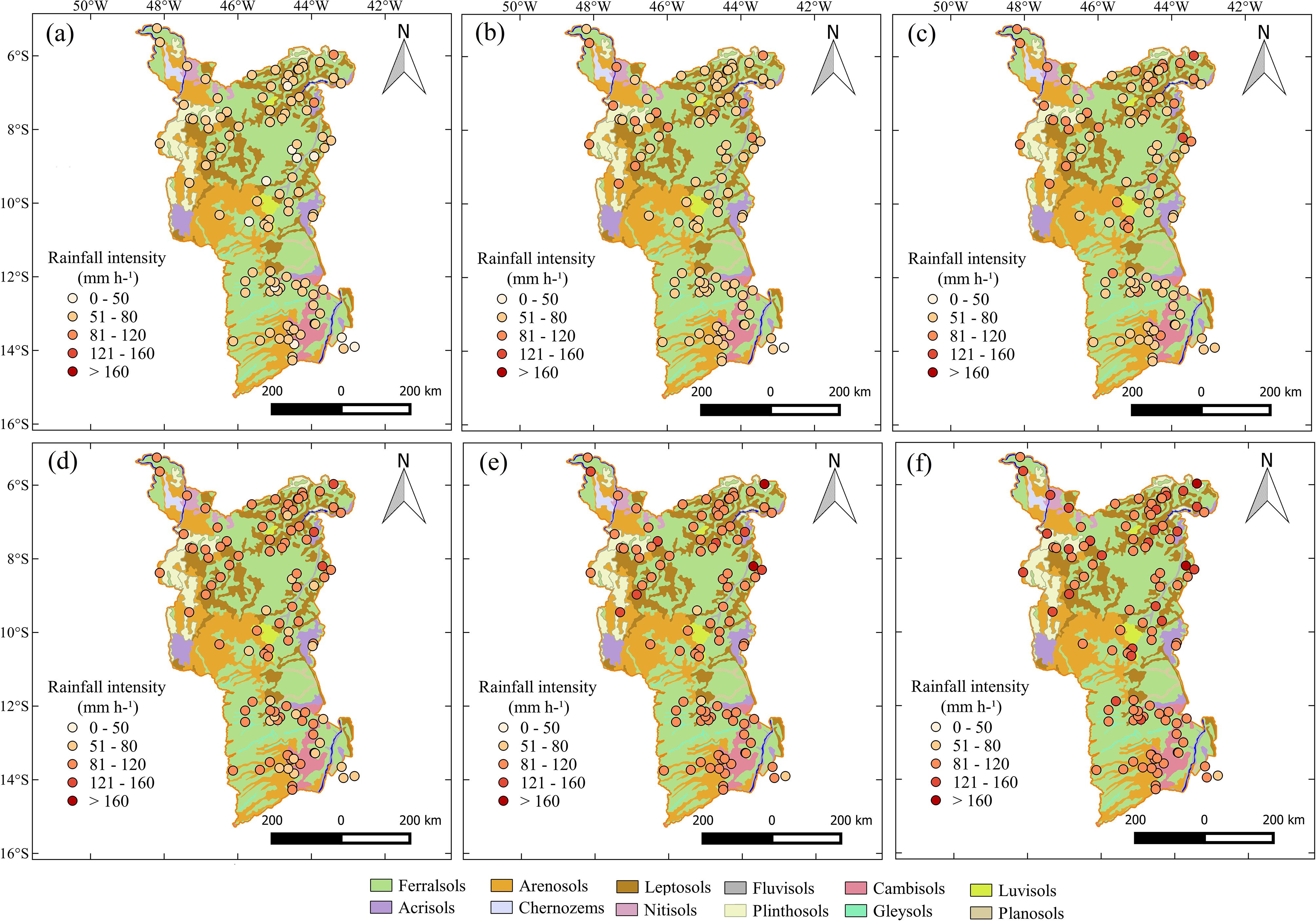
The most rainfall gauges had a rainfall intensity between 51 and 80 mm h-1, when considered return period of 2 years, with only two sites with rainfall intensity between 81 and 120 mm h-1 (Fig. 3a). There was an increase of sites with rainfall intensity between 81 and 120 mm h-1, from 2, for return period of 2 years, to 13, for return period of 5 years (Fig. 3b). The rainfall intensity between 121 and 160 mm h-1 had the first occurrence for return periods of 10 years in the northeast of the regions, with a total of two sites (Fig. 3c).
Simulated 30 minutes rainfall intensity for return periods of 2 (a), 5 (b), 10 (c), 25 (d), 50 (e) and 100 (f) years and the soils types in the MATOPIBA region. Adapted from IBGE (2012).
The most sites had rainfall intensity between 81 and 120 mm h-1 for return periods of 25 years (Fig. 3d). The rainfall intensity below 80 mm h-1 occurred only in three sites for return periods of 50 years, with most sites with rainfall intensity between 81 and 120 mm h-1. The first occurrence of rainfall intensity above 160 mm h-1 occurred in the return periods of 50 years in two sites in the northeast of the study regions (Fig. 3d). For return periods of 100 years, it was observed an increase of sites with rainfall intensity between 121 and 160 mm h-1 in relation to return periods of 50 years, mainly in the central-north (Fig. 3f).
In the central-north of MATOPIBA, the Intertropical Convergence Zone contributes for the highest rainfall intensity. The position of this convergence zone is affect by sea surface temperature in North and South Atlantic Sea. When the zone is under MATOPIBA, the rainfall is increase by convective of frontal systems originated from south and north hemisphere (Namias, 1972bNAMIAS, J. Influence of northern hemisphere general circulation on drought in northeast Brazil. Tellus, v. 4, p. 336-343, 1972.; Kousky, 1979KOUSKY, V.E. Frontal Influences on Northeast Brazil. Monthly Weather review, v. 107, p. 1140-1153, 1979.), and convective complex formed in the African region associated with anti-cyclones (Molion and Bernardo, 2002MOLION, L.C.B.; BERNARDO, S.O. A review of rainfall dynamics over northeastern Brazil. Revista Brasileira de Meteorologia, v. 17, p.1-10, 2002.). Otherwise, in the central-south of the MATOPIBA, the rainfall intensity is affected by frontal systems remained between 5° S and 18° S and local convective (Oliveira, 1986OLIVEIRA, A.S. Interações entre sistemas frontais na América do Sul e a convecção da Amazônia. Iin: Essay (Meteorology). INPE, São José dos Campos, 115 pp, 1986.), leading for lower rainfall intensity.
3.4.Erosion risk by erosivity and erodibility
The rainfall intensity of 50 mm h-1 occurred in the most rainfall gauges of MATOPIBA, when considered return periods of 2 year (Fig. 3). Nearing et al. (2017)NEARING, M.A.; YIN, S-Q.; BORRELLI, P.; POLYAKOV, V.O. Rainfall erosivity: An historical review. Catena, v. 157, p. 357-362, 2017. observed that the maximum energy for erosivity was reached when rainfall intensity was between 50 and 75 mm h-1, considering the methodologies of Universal Soil Loss Equation (USLE), Revised Universal Soil Loss Equation (RUSLE) and RUSLE 2. These conditions showed that, even under a low return period of two year, there was an event of maximum rainfall intensity that result in the maximum erosivity energy to cause soil erosion.
In the MATOPIBA, the main soil type were Ferralsols, Arenosol and Leptosols (Fig. 3). Ferralsols showed a mean (minimum-maximum) texture of 11% (1-37), 32% (6-82), 57% (5-90) and 1.09% (0.03-5.05), respectively, for silt, clay, sandy and organic matter content. These conditions lead an erodibility factor of 0.35 (Wanielista, 1978WANIELISTA, M.P. Stormwater management: Quality and quantity. Ann Harbor Science Publishers, Michigan, 383 pp, 1978.), classified as moderate risk (Jones et al., 1996JONES, D.S.; KOWALSKI, D.; SHAW, R.B. Calculating revised universal soil loss equations (RUSLE) estimates on Departament of Defense Lands: A review of Rusle factors and US Army Land Conditions- trend analysis (LCTA) data gaps. Departament of Forest Science, Colorado State University, Fort Collins, 9 p. 1996.). Leptosols also showed a moderate risk, with a mean texture of 30% (4-52), 22% (1-47), 48% (17-91) and 2.43% (0.16-6.12), respectively, for silt, clay, sandy and organic matter content. Arenosols had a low risk, due to higher sand content of 87% (71-99), and low content of silt and clay, respectively, of 6% (1-17) and 7% (0-18), although low organic matter content of 0.71% (0.02-5.55).
The erosivity showed higher potential for erosion, as well as, the moderate erodibility for areas with Ferralsols and Leptosols. This demonstrates the importance to reduce the risk of other compements from the Universal Soil Loss Equation. The Universal Soil Loss Equation consider the erosivity, erodibility, slope steepness and length, land use and cropping management, and control erosion practices (Nearing et al., 2017NEARING, M.A.; YIN, S-Q.; BORRELLI, P.; POLYAKOV, V.O. Rainfall erosivity: An historical review. Catena, v. 157, p. 357-362, 2017.). In these factors, the land use, cropping management and control practice are possible to be change to reduce erosion risk. The practices of zero tillage, mulching of crop residues and intercropping (Ward et al., 2018WARD, P.S.; BELL, A.R.; DROPPELMANN, K.; BENTON, T.G. Early adoption of conservation agriculture practices: Understanding partial compliance in programs with multiple adoption decisions. Land Use Policy, v. 70, p. 27-37, 2018.), construction of drains and culverts, contour drains and sowing, vegetation buffer, tree planting and land uses adequacy (Zwirtes et al., 2013ZWIRTES, A.L.; SPOHR, R.B.; BARONIO, C.A.; MENEGOL, D.R.; DA ROSA, G.M. et al. Soil water infiltration measuments using the double ring and cornell infiltrometer in a Rhodic Hapludix. Semina: Ciências Agrárias, v. 34, n. 6, p. 3489-3499, 2013.; Fernandez, 2017FERNANDEZ, M.A. Adoption of erosion management practices in New Zealand. Land Use Policy, v. 63, p. 236-245, 2017.) can be highlighted.
4.Conclusion
The maximum rainfall intensity was efficiently adjusted using the Gumbel probabilistic model for all rainfall gauges. Based on the Gumbel distribution model, the rainfall intensity-duration-frequency model had the parameters adjusted to estimate rainfall intensity for different duration and return period. The maximum rainfall intensity in 30 minutes for two year of return period showed a huge capacity to cause erosion, based on the maximum energy from erosivity. The erodibility risk was classified as moderate for Ferralsols and Leptosols, and low for Arenosols. The description of the maximum rainfall patterns through intensity-duration-frequency relationships can be used to dimension the size of the structure in agriculture areas and to adequate the land use, cropping management and control practice to reduce erosion, water losses and the vulnerability in rural areas.
References
- ALVARES C.A.; STAPE J.L.; SENTELHAS P.C.; GONçALVES J.L.M.; SPAROVEK G. Köppen’s climate classification map for Brazil. Meteorologische Zeitschirift, v. 22, p. 711-728, 2013.
- ANA - AGêNCIA NACIONAL DE áGUAS. Hidroweb Available at: [http://www.snirh.gov.br/hidroweb]. Accessed on: [April, 2014].
» http://www.snirh.gov.br/hidroweb - BEN-ZVI, A. Rainfall intensity-duration-frequency relationships derived from large partial duration series. Journal of Hydrology, v. 367, p. 104-114, 2009.
- BESKOW, S.; CALDEIRA, T.L.; MELLO, C.R. DE; FARIA, L.C.; GUEDES, H.A.S. Multiparameter probability distributions for heavy rainfall modeling in extreme southern Brazil. Journal of Hydrology: Regional Studies, v. 4, p. 123-133, 2015.
- CAMPOS, A.R.; SANTOS, G.G.; SILVA, J.B.L.; IRENE FILHO, J.; LOURA, D.S. Equações de intensidade-duração-frequência de chuvas para o estado do Piauí. Revista Ciência Agronômica, v. 45, p. 488-498, 2014.
- CARDOSO, C.O.; BERTOL, I.; SOCCOL, O.J.; SAMPAIO, C.A.P. Generation of intensity duration frequency curves and intensity temporal variability pattern of intense rainfall for Lages/SC. Brazilian Archives of Biology and Technology, v. 57, p. 274-283, 2014.
- CONAB. Survey of Crop Season Available at: [http://www.conab.gov. br/conteudos.php?a=1253&]. Accessed on: [January, 2018].
» http://www.conab.gov. br/conteudos.php?a=1253& - DAEE/CETESB - DEPARTAMENTO DE áGUA E ENERGIA ELéTRICA / COMPANHIA DE TECNOLOGIA DE SANEAMENTO AMBIENTAL. Drenagem urbana: Manual de projeto DAEE-CETESB, São Paulo, 466 pp, 1980.
- DAMé, R.C.F.; TEIXEIRA, C.F.A.; GONçALVES, T.; SANTOS J.P.S.; QUADRO, M.S. Erosividade sob duas durações de intensidades máximas da chuva em Pelotas - RS. Revista Agroambiental On-line, v. 6, p. 1-8, 2012.
- ELSEBAIE, I.H. Developing rainfall intensity-duration-frequency relationship for two regions in Saudi Arabia. Journal of King Sand University - Engineering Sciences, v. 24, p. 131-140, 2012.
- FERNANDEZ, M.A. Adoption of erosion management practices in New Zealand. Land Use Policy, v. 63, p. 236-245, 2017.
- IBGE. Interactive Maps: Soils Available at: [http://mapas.ibge.gov.br]. Accessed on: [February, 2012].
» http://mapas.ibge.gov.br - INMET. Clima - Normais Climátologicas do Brasil Available at: [http://www.inmet.gov.br/portal/index.php?r=clima/normaisClimatologicas]. Accessed on: [November, 2017].
» http://www.inmet.gov.br/portal/index.php?r=clima/normaisClimatologicas - JONES, D.S.; KOWALSKI, D.; SHAW, R.B. Calculating revised universal soil loss equations (RUSLE) estimates on Departament of Defense Lands: A review of Rusle factors and US Army Land Conditions- trend analysis (LCTA) data gaps Departament of Forest Science, Colorado State University, Fort Collins, 9 p. 1996.
- KOUSKY, V.E. Frontal Influences on Northeast Brazil. Monthly Weather review, v. 107, p. 1140-1153, 1979.
- KOUTSOYIANNIS, D.; KOZONIS, D.; MANETAS, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. Journal of Hydrology, v. 206, p. 118-135, 1998.
- MAPA - MINISTéRIO DA AGRICULTURA, PECUáRIA E ABASTECIMENTO. Projeções do Agronegócio no Brasil - 2016/17 a 2026/27 MAPA. Brasília, 86 pp, 2017.
- MAPA - MINISTéRIO DA AGRICULTURA, PECUáRIA E ABASTECIMENTO. Zoneamento Agrícola Available at: [http://www.agricultura.gov.br/assuntos/riscos-seguro/risco-agropecuario/portarias]. Accessed on: [August, 2018].
» http://www.agricultura.gov.br/assuntos/riscos-seguro/risco-agropecuario/portarias - MOLION, L.C.B.; BERNARDO, S.O. A review of rainfall dynamics over northeastern Brazil. Revista Brasileira de Meteorologia, v. 17, p.1-10, 2002.
- NAMIAS, J. Influence of northern hemisphere general circulation on drought in northeast Brazil. Tellus, v. 4, p. 336-343, 1972.
- NEARING, M.A.; YIN, S-Q.; BORRELLI, P.; POLYAKOV, V.O. Rainfall erosivity: An historical review. Catena, v. 157, p. 357-362, 2017.
- OLIVEIRA, A.S. Interações entre sistemas frontais na América do Sul e a convecção da Amazônia. Iin: Essay (Meteorology) INPE, São José dos Campos, 115 pp, 1986.
- OLIVEIRA, L.F.C.; ANTONINI, J.C.A.; FLOREZE, A.P.; SILVA, M.A.S. Métodos de estimativa de precipitação máxima para o Estado de Goiás. Revista Brasileira de engenharia Agrícola e Ambiental, v. 12, p. 620-625, 2008.
- OLIVEIRA, L.F.C.; CORTêS, F.C.; WEHR, T.R.; BORGES, L.B.; SARMENTO, P.H.L. Intensidade-duração-frequência de chuvas intensas para localidades o Estado de Goiás e Distrito Federal. Pesquisa Agropecuária Tropical, v. 35, p. 13-18, 2005.
- RADAM. Levantamento de recursos naturais Departamento Nacional da Produção Mineral (DNPM), Rio de Janeiro, 374 pp, 1974.
- TFWALA, C.M.; VAN RENSBURG, L.D.; SCHALL, R.; MOSIA, S.M.; DLAMINI, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Climate Risk Management, v. 16, p. 1-9, 2017.
- WANG, H.; GAO, J.E.; ZHANG, M-J.; LI, X-H.; ZHANG, S-L. et al Effects of rainfall intensity on groundwater recharge based on simulated rainfall experiments and a ground flow model. Catena, v. 127, p. 80-91, 2015.
- WANIELISTA, M.P. Stormwater management: Quality and quantity Ann Harbor Science Publishers, Michigan, 383 pp, 1978.
- WARD, P.S.; BELL, A.R.; DROPPELMANN, K.; BENTON, T.G. Early adoption of conservation agriculture practices: Understanding partial compliance in programs with multiple adoption decisions. Land Use Policy, v. 70, p. 27-37, 2018.
- WISCHMEIER, W.H.; SMITH, D.D.; UHLAND, R.E. Evaluation of factors in the soil-loss equation. Agricultural Engineering, v. 39, p. 458-462, 1958.
- WU, Z.; WEI, Y.; WANG, J.; XIA, J.; CAI, C. et al Effects of erosion degree and rainfall intensity on erosion processes for Ultisols derived from quaternary red clay. Agriculture, Ecosystems and Environment, v. 249, p. 226-236, 2017.
- ZHENG, M.G.; CHEN, X. Statistical determination of rainfall-runoff erosivity indices for single storms in the Chinese loess plateau. Plos One, v. 10, n. 3, e0117989, 2015.
- ZWIRTES, A.L.; SPOHR, R.B.; BARONIO, C.A.; MENEGOL, D.R.; DA ROSA, G.M. et al Soil water infiltration measuments using the double ring and cornell infiltrometer in a Rhodic Hapludix. Semina: Ciências Agrárias, v. 34, n. 6, p. 3489-3499, 2013.
Publication Dates
-
Publication in this collection
5 Aug 2019 -
Date of issue
Apr-Jun 2019
History
-
Received
04 June 2018 -
Accepted
31 Oct 2018