Abstract
The Brazilian design load standard still provides a wind speed map developed in 1977. Since then, new data have been collected and new charts have been proposed in literature. The literature not only alerts to changes in short-term wind gust patterns, but it also warns that the wind speed values are higher than observed in the past. Many researchers have suggested that these differences are correlated to climate change effects. Besides the geophysical and societal impacts of climate change, there is a general concern between designers on the impacts of higher wind speeds on structural design. This paper aims to analyze the wind speed as a stochastic variable and its influence on the design of steel structures when changes in wind speed occur. A stochastic approach is used to evaluate expected stress values for a steel beam-column example. A Monte Carlo analysis is performed on a forty-story steel frame to compare the impact of different wind speed scenarios and types of analysis. In the analyses, the wind speed is approached by a Gumbel distribution and future wind scenarios are generated for sensitiveness evaluation. The analytical and Monte Carlo analyses indicate that greater attention shall be given to the consequences of using an average wind speed value instead of a probability distribution function.
Keywords:
stochastic analysis; wind load; steel structures design
1. Introduction
All data or processes have a certain level of uncertainty. For example: material properties, loading scenarios, boundary conditions, geometry domain, etc., have smaller or larger uncertainties which influence the quantities or functions of interest (Deb et al., 2001). The probability theory can be applied to understand and quantify how these uncertainties impact these quantities or functions. When probability models are coupled as parameters in the differential equations that represent a physical problem of interest, the complete model is ruled by a stochastic differential equation (Dorini et al., 2011). Some examples using the probability theory to study the safety level of steel structures can be found in Beck & Doria (2008) and Zhao et al. (2011). The first study evaluated the reliability of I-section steel columns designed according to the Brazilian standard for the design of steel buildings NBR 8800 (ABNT, 2008). The second study evaluated the reliability associated to the use of a so-called Column Overdesign Factor (COF), which ensures a designer predefined preferable failure mode; this method is usually adopted in seismic structural design.
In this paper, however, the main focus is on the loading side, more specifically: wind load. Wind velocity and, hence wind load on structures, are stochastic processes, which fluctuate both in time and space (Beck & Corrêa, 2013). Generally, structural design codes consider the wind velocity randomness by defining a specific wind velocity value that is associated to a load factor; these values are determined based on a statistical study of the historical database of wind velocities.
Davenport (2002) named the steps to determine wind loading as a wind loading chain, which consists of assessing and combining the effects of: wind velocity, terrain roughness, geometric shape of the building, overall structural response to the local wind pressures, and dynamic amplification. This traditional approach, however, leads one to assume that each variable is deterministic and independent (Davenport, 2002). The Brazilian design standard, NBR 6123 (ABNT, 1988), recommends a similar approach. But the design chart of basic wind speeds of NBR 6123 (ABNT, 1988) is the one proposed by Padaratz (1977), which used the first database of maximum wind speed collected between 1950 and 1975 by Vieira Filho (1975). Since then, new wind speed records have been available and more stations have been built. It is worth mentioning that Santos (1989), Bautista (2002), Almeida (2010) and Beck & Corrêa (2013) presented new wind speeds studies and their charts are considerably different than the chart in the Brazilian standard NBR 6123 (ABNT, 1988).
Recently, scientists have raised global awareness on climate change patterns; the first IPCC (Intergovernmental Panel on Climate Change) report was published in 1990 and the last report was just released in 2014. All reports indicate important changes in environment patterns such as: seasonal temperature, amount of precipitation, wind speed, social impacts, etc. The PBMC (Brazilian Panel on Climate Change), funded by MCT and MMA (Ministry of Science and Technology and Ministry of Environment, respectively), has published a compilation of climate change impacts in the territory of Brazil (PBMC/GT1, PBMC/GT2, PBMC/GT3, 2013). These studies lead one to conclude that not only new wind speed charts have to be used, but also a new approach to take in account the wind speed variability needs to be developed to provide a reliable basis for structural design standards.
An alternative for taking into account the wind load variability is to consider the wind load as a stochastic variable adopted into the static or dynamic differential equations that governs a structural problem. The results of these equations are statistical moments (mean, standard deviation, etc.) and/or probability density function (pdf) of stress and displacement. That way, in a given scenario, non-deterministic variables are transformed into a probability function that describes stresses and strain in a structure. According to Dorini et al. (2011), two methods are available to solve stochastic differential equations:
-
the most formal method, which uses functional analysis to study the governing equation of a given problem with non-deterministic variables, and
-
one which uses numerical methods or mathematical techniques, such as Monte Carlo, to statistically understand the problem. Others techniques, based for example on Galerkin method, are discussed and presented in Ghanem (1999), Deb et al. (2001), BabuŠka et al. (2004), Wan & Karniadakis (2006), Ma & Zabaras (2008) and Azevedo (2009).
The purpose of this paper is to analyze, through a simple example, the impact of the wind load - non-deterministic variable - on the static equilibrium equations of a beam-column and to determine if the same conclusions can be expanded to the analysis of typical steel-frame buildings. Based on the functional analysis method presented in Dorini et al. (2011), analytical solutions for equilibrium of a beam-column in the straight and deflected shape were obtained; expected values in both analyses were compared with the classical deterministic procedure. Probability density function stress curves are also generated for different wind speed scenarios. A Monte Carlo analysis of a typical high-rise steel-frame building was performed; different types of structural analysis procedures were adopted to verify the consistency of the conclusions.
2. Methods
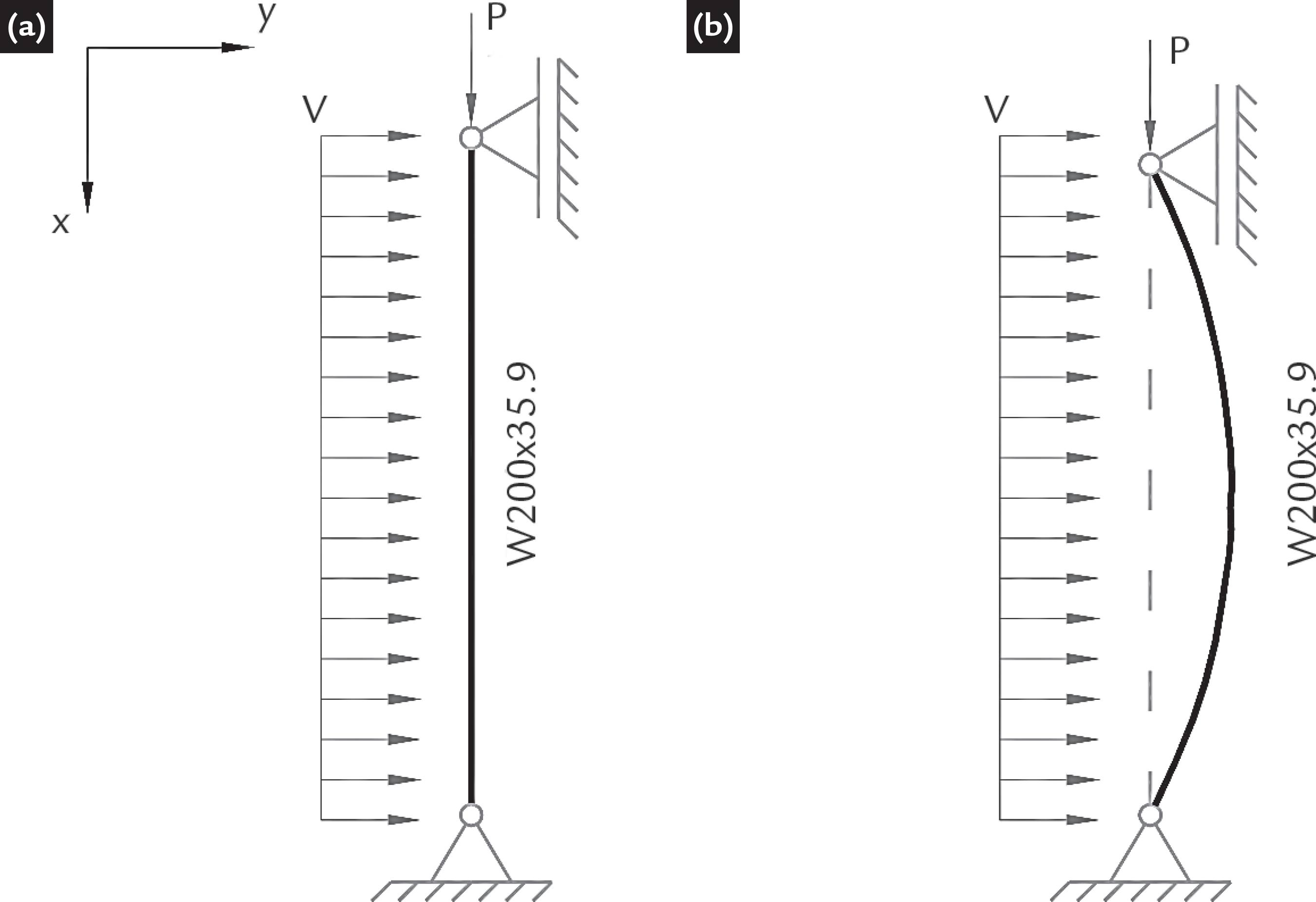
Herein, the wind load is considered as a stochastic variable governed by a given probability density function, which is followed by examples that evaluate the stress probability function of a beam-column - equilibrium in the original (perfectly straight) and deflected shape. A comparison between expected stress value and stress obtained from mean wind speed value for a given artificial future scenarios is also presented. The stochastic analysis is performed for the beam-column example depicted in Figure 1.
Typical steel beam-column: W 200 x 35.9. a) Beam-column in perfectly straight shape. b) Beam-column in deflected shape due to the bending moment (wind load).
Wind load as a stochastic variable
The wind load (pressure) is proportional to its velocity. As the wind speed is a random variable, the load will also be a random variable, then:
where α depends on the structural geometry (deterministic variable) and ω is a random event. The wind velocity can be modeled using a Gumbel cumulative distribution function:
where 𝑢 is the location parameter and α is a scale parameter. Deriving Eq. 2 with respect to 𝑣, probability density function (pdf) is obtained. The expectation operator (mean) E [ ∙ ] is defined as:
where C'𝑣 (𝑣) is the wind speed pdf. For Gumbel distribution E [𝑣]=𝑢 + γα, where γ is the Euler-Mascheroni constant (≈0.5772).
Equilibrium in the original (perfectly straight) shape
The maximum column stress (design value) in Figure 1 occurs at the column mid-height. It is assumed that superposition can be used. Then, the total stress is the sum of two parts: stresses caused by the wind load and stresses caused by the vertical force, which can be written in the general form:
where σT,s (ω) is the random total stress, bs is the bending moment and c(P) the normal stress from the vertical (deterministic) force P. The subscript s will be used herein when the variable is associated to the column in a perfectly straight shape, Figure 1(a). Thus, the cumulative distribution function for σT,s (ω) is:
for bs>0, q-c(P)≥0 and for some realization q of the total stress. As shown in Eq. 5, the total stress function also follows a Gumbel distribution.
Equilibrium in the deflected shape
Herein, we solve the second order elastic equation considering the bending moment produced by the vertical force:
where 𝑦(𝑥,ω) is the lateral deflection. Solving this equation for a random event ω, we have the expression for the bending moment, which is non-linear in respect to the vertical force P. We can also use the superposition of axial and bending axis stresses to get the maximum stress:
The subscript d will be used herein when the variable is associated to the column in a deflected shape, Figure 1(b). The cumulative distribution function for σT,d (ω) is obtained through the same approach of Eq. 5:
for bd(P)>0, which bd (P) is non-linear in respect to the vertical force P, q-c(P)≥0 and for some realization q of the total stress. Note that equilibrium in the deflected shape also leads to a total stress function, which follows a Gumbel distribution.
Stress values comparison
The difference between the expected stress value based on stress probability density function (E [σT,𝑖 ]) and the stress value calculated with expected basic wind speed (σ-T,𝑖 ) is evaluated in this section. The equations for comparison are:
where the index i is either s (perfectly straight) or d (deflected shape), the pdf C'σT,𝑖 is given in Eq. 5 or in Eq. 8. Equation 9 can be written as (using the expressions for σ-T,𝑖 and C'σT,𝑖:
in which the difference between σ-T,𝑖 and E [ σT,𝑖 ] is clear.
Wind speed scenarios
PBMC/GT2 (2013) reported a 2°C increase in the global temperature, which directly and critically impacts our ecosystems, as well as, generating a change in extreme event patterns and intensity. The first hurricane observed in the South Atlantic region occurred in 2004 and in the last 50 years the south region of Brazil has registered an abrupt increase in the precipitation volume. Pereira et al. (2013) analyzed trends in wind speed from some national weather station data series and examined wind forecasts from the circulation model (GCM); their analysis was based on an average wind speed value. Important developments were achieved in terms of numerical tools to predict the effects of the climate change, but the level of uncertainties is still large.
Based on the study presented in Steenbergen et al. (2009), it was assumed, Table 1, the parameters 𝑢 and α for the Gumbel distribution to analyze the impact of a non-deterministic wind load on a steel structure; these values are used in the next section.
3. Beam-Column Example - Results and Discussions
The results and discussions presented in this subsection are based on the study of the beam-column depicted in Figure 1. The parameters for the Gumbel functions are: 𝑢 = 45 m/s, α = 2 m/s, and the linear factor α = 12.0 (air density, pressure area, pressure factor, etc). The comparison between the probability density functions derived above (equilibrium in the straight and deflected shape) is depicted in Figure 2 below:
Probability density function of total stress (SI units) for equilibrium in the straight and deflected shape.
Figure 2 depicts that, for an increase in the vertical force, the probability density function for equilibrium in the deflected shape shifts to higher stress values, while the probability of the peak load decreases and the curve becomes wider - larger standard deviation. Table 2 summarizes the comparison between the deterministic and stochastic expected stress for a beam-column with axial load, P, where equilibrium is given in the original (straight) shape and in the deflected shape (Eq. 9 and Eq. 10). The parameter α is equal to 10 m/s.
Table 2 indicates that the expected stress values are greater for stochastic analysis and that equilibrium in the deflected shape, as expected, leads to higher stress values. Note that the ratios between the stochastic and deterministic expected values are practically the same for each type of equilibrium analysis.
Figure 3 depicts the pdf for different wind scenarios and vertical force P = 3,000. Figure 3 depicts that parameters 𝑢 and α shift to higher values and the function baseline gets wider. Table 3 provides the ratio between expected stress values. The results indicate a nonlinearity between wind speed and stress, as expected, since wind load and wind speed have a nonlinear relationship. Equilibrium in the straight and the deflected shape produces practically the same expected stress ratio, since, for this column-beam example, wind load and stresses have a linear relationship.
4. Frame Example - Results and Discussions
A forty-story steel frame commonly found in office-type building is analyzed in this section; this frame, Figure 4, is a two-bay structure with 9.15m span (30 feet), 9.15m (30 feet) spacing between frames, and each story is 3.66m (12 feet) high. Cross-sections, mechanical material properties, and nominal loads are summarized in Figure 4. This frame was originally proposed in a report issued by the Fritz Laboratory at Lehigh University, Lu et al. (1975), with the intention of investigating the behavior and resistance of typical multistory steel frames. Since then, researchers have used the frames described in the report as benchmark problems for further studies.
Description of forty-story steel frame (Adapted from Lu et al. (1975) and Stlater et al. (2011)).
The finite element model of the forty-story steel frame considers that the load factor for dead load is 1.2, while the load factor is 0.5 for live load; a load factor was not applied to the wind load since the wind load is considered as a non-deterministic variable in the model. The simulation was performed using the structural analysis software MASTAN2 (Ziemian, 2009), following the recommendations listed in Stlater et al. (2011), which are:
-
residual stresses, as well as connection size and stiffness were neglected for simplicity,
-
all distributed loads were lumped to beam-column intersections using tributary area (lengths),
-
self-weight was assumed to be included in the dead loads provided,
-
all wide-flange sections are oriented for major-axis flexure (i.e., with their webs in the plane of the frame),
-
all out-of-plane behavior is restrained,
-
member lengths are defined by their centerlines,
-
to adequately account for P-δ effects, members are divided into four elements,
-
second-order analyses were performed using a predictor-corrector (mid-point Runge-Kutta) solution scheme and applying the factored loads in 5% increments until the frame is fully loaded.
In this paper, the considered forty-story steel frame is located in the region of Campinas, Sao Paulo, Brazil. Based on historical data available in the software Mathematica (2015) for the airport of Viracopos (VCP) from 1973 to 2014, it was found that the basic wind speed distribution is well represented by a Gumbel distribution function with location parameter 𝑢 = 35.8m/s (80mi/h) and scale parameter α = 4m/s (8.95mi/h). As an example, a basic wind speed of 35.8m/s (80mi/h) is equivalent to a mean velocity pressure of 778N/m2 (16.25lbf/ft2), given that the factors to account for the importance of the structure, its height, and the terrain (ASCE 7-10, 2010) are equal to 1. Given the Gumbel distribution function just described, a vector with 10,000 values of basic wind speed was created and for each value of basic wind speed, three types of analysis were performed:
-
first-order elastic,
-
second-order elastic, and
-
second-order inelastic; for more details on what each type of analysis entails, the reader is directed to McGuire et al. (2000). A comparative histogram of the moment at the base of the center column is presented in Figure 5. The moment at the base of the center column was chosen as the variable to be analyzed, since it is the highest overturning moment found in the model and, thus, can provide a good understating of the comparisons between the different types of analyses performed on the proposed forty-story steel frame structure.
Figure 5 and Table 4 depict that, as was concluded for a beam-column analytical analysis, the histogram for second-order analysis shifts to a higher moment at the base, while the probability of the maximum moment decreases and the curve becomes wider - larger standard deviation; note that the ratios between the Monte Carlo simulation and the analysis using the expected basic wind speed value are still practically the same for each type of analysis. Another interesting fact is depicted in the zoomed-in view graph in Figure 5; for most part of the models, the probability associated to second-order elastic and inelastic analysis is the same. However, once the moment at the base reaches values close to 4,210.1N.m, second-order elastic and inelastic analysis looses its parity. The moment value just mentioned is the moment at the base right before the structure reaches a plastic collapse mechanism, which can only be detected through a second-order inelastic analysis. In fact, based on the second-order inelastic analysis, 0.21% of the structures collapse under the applied wind pressure distribution; this value can be considered high, given that an acceptable probability failure is in the order of 10-4; this observation reinforces that more studies shall be conducted on the topic and that a proper reliability analysis - all non-deterministic variables are considered/varied in the analysis - is necessary given the actual climate change scenarios that we are experiencing.
5. Conclusion
How to perform a stochastic analysis for a very simple example: steel beam-column has been described. Results indicate that, using Gumbel distribution to describe the wind velocity, the expected stress values are higher when performing a stochastic analysis. It was also shown that the probability density functions are more susceptible to vertical force changes when equilibrium is considered in the deflected shape, which shows the importance of also accounting for the vertical force in a stochastic analysis.
There were significant changes in the pdf curves for different wind speed scenarios, as well as changes in the expected stress ratio (higher stress values and larger standard deviation), much due to the nonlinearity between wind speed and stress; similar conclusions were reached in the analysis of a multi-story high-rise steel frame. The importance of further research in this area has been shown in a beam-column model, as well as in a high-rise building model, where the effect of the basic wind speed was considered separately without the interference of any other non-deterministic variable. Climate change has affected the loading curve distribution, especially for wind loads, and future changes must be acknowledged in upcoming design standards.
6. Acknowledgements
The authors would like to acknowledge SimWorx - Eng., Research & Development and College of Civil Engineering, Architecture and Urbanism - University of Campinas for supporting this research project and Patrick Kherlakian for his assistance with MASTAN2/Matlab. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors only.
7. References
- ABNT (2008). "NBR 8800: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios." Associação Brasileira de Normas Técnicas
- ALMEIDA, L. O.. Estudo para atualização do mapa de ventos da NBR6123 Brasil, São José dos Campos: ITA, 2010. (M.Sc. Thesis).
- ASCE. Minimum design loads for buildings and other structures. ASCE/SEI 7-10. Reston, VA, American Society of Civil Engineers, 2010.
- AZEVEDO, J. S.. Modelagem numérica de escoamento transiente em meios porosos aleatórios usando a expansão de Karhunen-Loève Brasil, Salvador: D.Sc. UFBA, 2009. (D.Sc. Thesis).
- BABUŠKA, I., TEMPONE, R., ZOURARIS. G. E. Galerkin finite element approximations of Stochastic Elliptic Partial Differential Equations. SIAM J. Numer. Anal., v. 42, n. 2, p. 800-825, 2004.
- BAUTISTA, E. A.L. A distribuição generalizada de valores extremos no estudo da velocidade máxima do vento em Piracicaba Brasil, Piracicaba, SP: USP, 2002. (M.Sc. Thesis).
- BECK, A. T., CORRÊA, M. R. S. New design chart for basic wind speeds in Brazil. Latin American Journal of Solids and Structures , v. 10, p. 707-723, 2013.
- BECK, A. T., DÓRIA, A. S. Reliability analysis of I-section steel columns designed according to New Brazilian Building Codes J. of the Braz. Soc. of Mech. Sci. & Eng., v. XXX, n. 2, p. 152-159, 2008.
- BUCHER, C. Computational analysis of randomness in Structural Mechanics London, UK: Taylor & Francis Group, 2009. v.3.
- DAVENPORT, A. G. Past, present and future of Wind Engineering. Journal of Wind Engineering and Industrial Aerodynamics v. 90, p. 1371-1380, 2002.
- DEB, M. K., BABUŠKA, I., ODEN, J. T. Solution of Stochastic Partial Differential Equations using Galerkin Finite Element Techniques, Comput. Methods Appl. Mech. Engrg., v. 190, p. 6359-6372, 2001.
- DORINI, F. A., CUNHA, M. C. C., Oliveira, S. P. Soluções de problemas envolvendo equações diferenciais sujeitas a incertezas. TEMA Tend. Mat. Apli. Comput. v.12, n.2, p. 111-123, 2011.
- GHANEM, R. Ingredients for a general purpose stochastic finite elements implementation. Comput. Methods Appl. Mech. Engrg. v. 168, p. 19-34, 1999.
-
Intergovernmental Panel on Climate Change. IPCC Fifth Assessment Report - Climate Change 2013. 2013. Available at www.ipcc.ch Accessed August 2014.
» www.ipcc.ch - LU, L.W., OZER, E., DANIELS, J.H., OKTEN, O.S., MORINO, S. Frame stability and design of columns in unbraced multistory steel frames, Fritz Engineering Laboratory Report n. 375.2. Lehigh University, Bethlehem, Pennsylvania: Lehigh University, 1975.
- MA, X., ZABARAS, N. A stabilized stochastic finite element second-order projection method for modeling natural convection in Random Porous Media. Journal of Computational Physics v. 227, p. 8448-8471, 2008.
- MCGUIRE, W., GALLAGHER, R. H., ZIEMIAN, R. D. Matrix structural analysis 2000.
- NBR 6123:1988: Forças devidas ao vento em edificações. ABNT - Associação Brasileira de Normas Técnicas, Rio de Janeiro.
- PADARATZ, I. J. Velocidade básica do vento no Brasil Brasil, Porto Alegre, RS: UFRGS, 1977. (M. Sc. Thesis).
- PBMC, Contribuição do Grupo de Trabalho 1 ao Primeiro Relatório de Avaliação Nacional do Painel Brasileiro de Mudanças Climáticas. Sumário Executivo GT1, PBMC, Rio de Janeiro, Brazil. 2013.
- PBMC, Contribuição do Grupo de Trabalho 2 ao Primeiro Relatório de Avaliação Nacional do Painel Brasileiro de Mudanças Climáticas. Sumário Executivo GT2, PBMC, Rio de Janeiro, Brazil. 2013.
- PBMC, Contribuição do Grupo de Trabalho 3 ao Primeiro Relatório de Avaliação Nacional do Painel Brasileiro de Mudanças Climáticas. Sumário Executivo GT3, PBMC, Rio de Janeiro, Brazil. 2013.
-
PEREIRA, E. B., MARTINS, F. R., PES, M. P., da CRUZ SEGUNDO, E. I. LYRA, A. A. The impacts of global climate changes on the wind power density in Brazil. Renewable Energy v. 49, p. 107-110. doi:10.1016/j.renene.2012.01.053, 2013.
» https://doi.org/10.1016/j.renene.2012.01.053 - SANTOS, M. L. W. Regionalização das velocidades extremas e temperaturas dos ventos no Centro-Sul do Brasil Brasil, Porto Alegre: UFRGS, 1989. (M.Sc. Thesis).
- STATLER, D.E., ZIEMIAN, R.D., ROBERTSON, L.E.. The natural period as an indicator of second-order effects. Proceedings of the Annual Stability Conference Structural Stability Research Council 2011.
- STEENBERGEN, R. D. J. M., GEURTS, C. P. W., VAN BENTUM, C. A. Climate change and its impact on structural safety. HERON Built Environment and Geosciencesv. 54, n. 1, 2009.
- VIEIRA FILHO, J. M. S. Velocidades máximas do vento no Brasil Brasil, Porto Alegre, 1975. (M.Sc. Thesis).
- WAN, X. KARNIADAKIS, G. Multi-element generalized polynomial chaos for arbitrary probability measures. SIAM J. Sci. Comput. v. 28, n. 3, p. 901-928, 2006.
- WOLFRAM Research, Inc., 2015. Mathematica, Version 10.2, Champaign, IL.
- ZHAO, Y.-G., SHARFUDDIN, M., IDOTA, H. Probabilistic evaluation of COF for steel frames considering system reliability. J. Struct. Constr. Eng., AIJ. v. 76, n.665, p. 1235-1244, 2011.
-
ZIEMIAN, R. D. & MCGUIRE, W. 2009. MASTAN2. Available at www.mastan2.com Accessed December 2015.
» www.mastan2.com
Publication Dates
-
Publication in this collection
Apr-Jun 2016
History
-
Received
21 Dec 2015 -
Accepted
01 Mar 2016

 A stochastic approach for the wind load effect on steel structures
A stochastic approach for the wind load effect on steel structures