Abstract
Estimation of some mineral deposits involves chemical species or a granulometric mass balance that constitute a closed constant sum (e.g., 100%). Data that add up to a constant are known as compositional data (CODA). Classical geostatistical estimation methods (e.g., kriging) are not satisfactory when CODA are used, since bias is expected when estimated mean block values are back-transformed to the original space. CODA methods use nonlinear transformations, and when the transformed data are interpolated, they cannot be returned directly to the space of the original data. If these averages are back-transformed using the inverse function, bias is generated. To avoid this bias, this article proposes geostatistical simulation of the isometric logratio ratio (ilr) transformations back-transforming point simulated values (instead of block estimations), with the averaging being postponed to the end of the process. The results show that, in addition to maintaining the mass balance and the correlations among the variables, the means (E-types) of the simulations satisfactorily reproduce the statistical characteristics of the grades without any sort of bias. A complete case study of a major bauxite deposit illustrates the methodology.
Keywords:
compositional data; isometric transformations ratios (ilr); simulation; closure
1. Introduction
Mineral deposits such as iron ore, bauxite, and phosphate are characterized by containing, in addition to the main elements (Fe2O3, Al2O3, P2O5, etc.), other elements or chemical species with effects on economic viability, industrial processes, or mine planning. It is common to estimate multiple elements, possibly correlated and sometimes with a combination of contents that must sum to a particular figure (e.g., 100%). According to Aitchison (1981), data that add up to a constant are termed compositional data (CODA), and they carry information that is relative and not absolute. This condition of summation to a constant implies that the estimates should also sum to a constant.
When working with multi-element deposits and, furthermore, having to deal with CODA, which are not necessarily physically correlated (spurious correlation; Pearson, 1897), it is not possible to use traditional methods to achieve closure of the mass balance of the multiple chemical species or physical variables. Thus, to overcome this inconsistency, it is typically necessary to perform post-processing, such as proportional distribution of the error of closure between the different granulometric fractions for each of the estimated elements.
Classical geostatistical methods such as ordinary kriging (Matheron, 1963) may be appropriate for the best local estimate of a single variable, ignoring its spatial interdependence with other correlated attributes. Each variable is estimated separately (in the case of ordinary kriging) with its specific parameters of spatial continuity, which leads to different weights being obtained for each attribute and a failure to obtain estimates that satisfy the constant-sum constraint. In the case of ordinary cokriging (Marechal, 1970), which takes into consideration the correlation between multiple variables, closure can only be ensured when working with an intrinsic coregionalization model (ICM). However, the model used as reference for the direct and cross variograms is rarely adjusted adequately for all variables. When a linear coregionalization model (LCM) is used, the complexity of modeling the variogram increases with the number of variables and also fails to ensure the closure balance.
Aitchison (1986) developed two transformations to deal with CODA, ensuring that any operation applied to the transformed data sums to a constant after these data are back-transformed to the original space. These transformations are known as additive logratio transformations (alr) and centered logratio transformations (clr). Egozcue et al. (2003) defined new transformations, called isometric logratio transformations (ilr), which are used in this article. A fundamental feature of the methods mentioned is the use of nonlinear transformations (logarithms).
Pawlowsky et al. (1995) and Odeh et al. (2003) applied alr cokriging and univariate ordinary kriging, respectively, to predict composition at unsampled locations. They used the inverse transformations (agl) to back-transform the elements of the estimated variates. However, this back-transform is biased (the average data transformed by a nonlinear function cannot be back-transformed by a linear function (OK) without generating a bias) and a solution for an unbiased back-transform is unknown (Pawlowsky-Glahn and Olea, 2004).
Bragulat et al. (2002), Bragulat and Sala (2003), and Boezio et al. (2012) used kriging and cokriging of logratio transformations applied to mineral deposits. They also used the inverse transformations in the estimated variables, but a problem appears when this type of transformation is used in the estimation process, since the average kriged block values cannot be back-transformed without biasing the estimated grades. To solve this problem, Pawlowsky-Glahn and Olea (2004) suggested a numerical approximation to generate unbiased estimates in the inverse transformations of CODA. This approximation is obtained through the use of the Gauss-Hermite procedure (Lark and Bishop, 2007; Ward and Muller, 2012; Delgado et al., 2012).
This paper presents an alternative way to deal with transformed data (ilr) and avoid bias in the back-transformation, i.e., geostatistical simulations. The main idea is to back-transform simulated points on a closely spaced grid (instead of estimated blocks) to the original space (at point support), postponing the averaging into larger volumes (blocks) to the end of the process. Furthermore, it is proposed that closure of the sum on chemical and granulometric variables be ensured at each simulated block, thereby reproducing the correlations between them. A complete case study of a major bauxite deposit illustrates the methodology.
2. Methodology
2.1 Compositional data analysis (CODA)
A composition of D parts is a vector x=[x1,x2,...,xD] all of whose components are strictly positive numbers and carry only relative information. This information is conditioned to sum of a constant and represents parts of a whole, for example, unit (1), percent (100%), or parts per million (ppm). Pawlowsky-Glahn and Buccianti (2011) define the sample space containing the compositional data as the D-simplex.
where the components of each vector in SD are called the parts of the composition. The operation that defines the closure of a composition in a constant k is given by
where
C(Z) is the closure operation;
k is the closure constant (generally 100%);
Zi is the value of the ith sample.
2.2 Isometric logratio transformation (ilr)
Before defining the transformation (ilr), it is necessary to understand the concept of an orthonormal basis. As in any Euclidean space, there are an infinite number of orthonormal bases in SD that can be obtained by various methods, for example, the Gram-Schmidt procedure mentioned by Egozcue et al. (2003) or the singular value decomposition (SVD) procedure described by Pawlowsky-Glahn et al. (2010). Pawlowsky et al. (2005) proposed a new method for obtaining an orthonormal basis, known as sequential binary partition (SBP).
The SBP is defined by Egozcue et al. (2005) as a hierarchy of parts of a composition for obtaining particular orthonormal coordinates. In the first order of the hierarchy, all parts are divided into two binary groups (+1 and -1). In the following steps, each group is divided into two new groups, and the process continues until all groups have a single part. The number of binary partitions at the end of the process is D - 1 (where D is the number of dimensions, corresponding to the number of variables per fraction). Table 1 shows an example of the SBP applied to a composition of five parts.
Sequential binary partition of a five-part composition (P1,…,P5), where r(+) represents addition of positive 1’s (+1) and s(−) represents addition of negative 1’s (−1).
As proposed by Egozcue et al. (2003), the isometric logratio transformation of the ith composition is defined by
where
ilri = ilr transformation for ith composition;
r = sum of the positive 1's (+1) in the SBP;
s = sum of the negative 1's (-1) in the SBP;
(xi1 xi2...xir)1⁄r = geometric mean of the variables that were selected with (+1) in the SBP;
(xj1 xj2...xjs)1⁄s = geometric mean of the variables that were selected with (-1) in the SBP.
This new transformation will have D - 1 dimensions for each composition analyzed, depending on the number of original variables.
The next step consists in using geostatistical simulation methods for each transformation (ilr). In this specific study, the turning bands algorithm (Matheron, 1973) was used to run simulations in multi-Gaussian space. Various alternative simulation methods are available in literature (Deutsch and Journel, 1998), but the one chosen here proved to be efficient for the purpose of the study. At the end of the process, each simulation is back-transformed to the space of the original data by an inverse isometric logratio transformation given by
where
ilr-1 = back-transformation;
x = simulated value for the transformation (ilr);
ψ = matrix constructed from the SBP;
C = closure operation (equation (2)).
The construction of the matrix ψ is based on the SBP that was initially defined. Each partition will have its own matrix depending on the number of variables. This new matrix is calculated as follows:
where ψi+ and ψi- represent the values of the matrix ψ defined as +1 and -1 in the SBP, and ri and si represent the sums of +1 and -1 obtained in the same partition. For the example presented in Table 1 corresponding to an SBP of five parts, the matrix ψ is defined in Table 2.
2.3 Case study
The case study corresponds to a data set from a bauxite deposit located in the Brazilian Amazon (Figure 1).
The variables correspond to three granulometric fractions (percentages of the total mass retained at given sieves during screening tests). These variables are defined as recoveries at the following fractions: +14# (REC14), +400# (REC400), and -400# (REC-400). Each variable is defined as the percentage of the mass retained on each sieve, and the sum of the variables for each analyzed sample should be 100%. However, there are some errors associated with sampling (Abzalov, 2011) that prevent that the sum of the variables analyzed from closing to a constant. In this particular case, these errors were not greater than ±3%. Therefore, to start the analysis of the CODA, the closure operation given in equation (2) was applied.
The isometric logratio transformation was subsequently applied for each of the compositions of the three analyzed variables. This transformation led to a two-dimensional sample space, in which the variables were called ilr1 and ilr2. Each variable was independently simulated, considering their spatial continuity models and search parameters. The total number of simulations was 30 for each variable (number of realizations sufficient to map uncertainty due to the standardization of the variance of the means). The final estimate was taken to be the E-type (average) of these 30 simulations. Figure 2 shows a suitable procedure for working with CODA without generating bias by back-transforming block estimations. Note that the average of the simulated blocks (50x50x0.5)m is obtained after the punctual simulations (10x10x0.5)m are back-transformed by the inverse function ilr-1 (step 7).
Procedure for using the transformation (ilr) without generating bias in the average blocks that are back-transformed.
3. Results
Each simulation generated was validated by the reproduction of the basic statistics of the original data, the variogram model, and the correlations among the variables. Table 3 shows a statistical summary of the original data and the upscaled results for two realizations selected randomly (Nos. 4 and 24). Note that these simulations, like the others, satisfactorily reproduce the general characteristics of the analyzed variables, not exceeding the minimum and maximum values of the original data and with a relative error in the average not exceeding 5%.
Figure 3 shows the non-ergodic correlogram model of the original data (red) and those for the 30 realizations (green) corresponding to the variables Rec14, Rec400, and Rec-400. Note that for all variables, the model satisfactorily reproduced the ergodic fluctuations. For modeling spatial continuity, a non-ergodic correlogram was used (Srivastava, 1987). Table 4 shows correlation matrices between the original variables (a) and the E-type simulations (b). Note that the correlation of the E-type simulations between the variables Rec14 and Rec400 showed a small increase of 0.1. This small increase is a characteristic resulting from the smoothing effect generated by the E-type model (as in kriging).
Spatial continuity models for the original data (red) and simulations (green), obtained using a non-ergodic correlogram: (a) Rec14; (b) Rec400; (c) Rec-400.
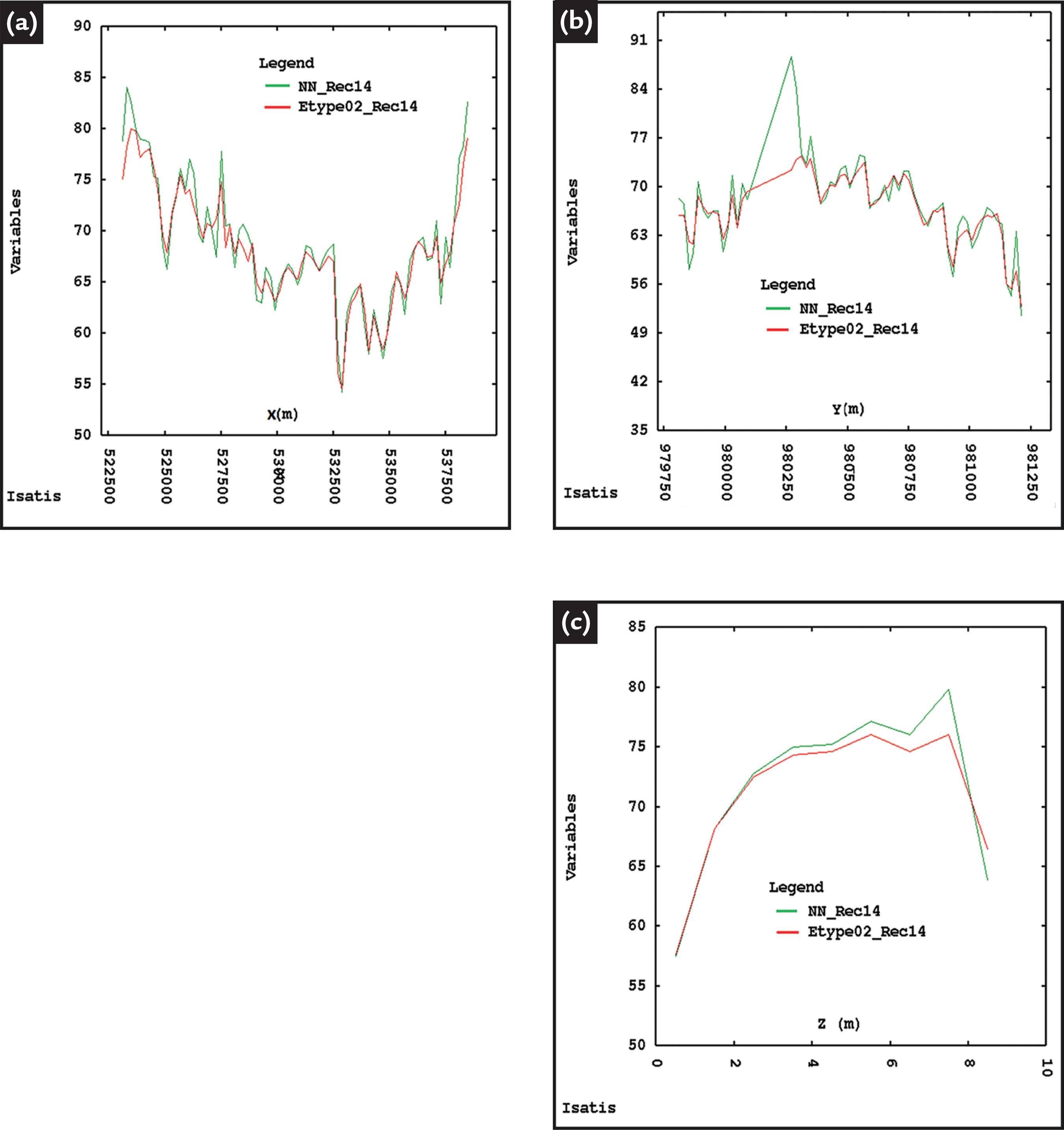
A final validation was carried out through checking the local average reproduction (swath plot) by comparing the block grade means versus the declustered data means for each variable respectively. The plots check the E-type model derived from 30 simulations. Figure 4 shows the local averages of the variable Rec14 along the East-West, North-South, and vertical (Z) directions. Note that the model and data mean show good adherence along all directions.
Swath plot for the variable Rec14 comparing grades from the E-type models (red line) and the declustered data local mean (green line) along (a) the East-West, (b) the North-South, and (c) the vertical (Z) directions.
Finally, the closure of the estimated masses retained on each sieve was analyzed. This closure is given by the sum of the percentages retained at the three granulometric fractions at each simulated point. Figure 5 shows the histograms for the closure values at each block for three randomly selected simulations (Nos. 8, 15, and 21). Note that in each case, the closure was at 100%; that is, the sum of the percentages of the total mass at each simulated node was guaranteed to be constant.
Histograms for the closure (sum of the percentages of the total mass for each granulometric fraction) of the simulations: (a) No. 8; (b) No. 15; (c) No. 21.
4. Conclusion
Simulations of the transformation (ilr) have shown it to be an alternative tool for dealing with compositional data on multi-element mineral deposits for several reasons. It avoids bias in direct kriging of blocks of nonlinearly transformed data by retaining the E-type of multiple simulations. The simulations are satisfactorily validated by the data statistics: they satisfactorily reproduce the basic statistics of the original data, the model of spatial continuity, and the correlations between variables, and they exhibit good adherence between E-type block values and the local data average. All the simulations ensured the granulometric closure of the masses retained on each sieve (100%) at each grid node or block (after upscaling).
5. References
-
ABZALOV, M. Sampling errors and control of assay data quality in exploration and mining geology. In: IVANOV O. (Ed.). Applications and experiences of quality control. InTech. http://www.intechopen.com/books/applications-and-experiences-of-quality-control/sampling-errors-and-control-of-assay-data-quality-in-exploration-and-mining-geology, 2011. 35p.
» http://www.intechopen.com/books/applications-and-experiences-of-quality-control/sampling-errors-and-control-of-assay-data-quality-in-exploration-and-mining-geology - AITCHISON, J. A new approach to null correlations of proportions. Mathematical Geology, v. 13, n. 2, p. 175-189, 1981.
- AITCHISON, J. The statistical analysis of compositional data. Chapman & Hall, London, v. 44, n. 2, p. 139-177, 1986.
- BOEZIO, M.N., COSTA, J. F. C., KOPPE, J. C. Cokriging of additive log-ratios (alr) for grade estimation in iron ore deposits. REM - Revista Escola de Minas, Ouro Preto, v. 65, n. 3, p. 401-411, 2012.
- BRAGULAT, E.J. & SALA, C. H. Comparison of kriging results of regionalised compositional data using three different data transformations. Case study: bauxites in Hungary Spain: Universitat Politècnica de Catalunya (UPC), 2003. 6p.
- BRAGULAT, E. J., SALA, C. H. & DIBLASI, A. M. An experimental comparison of cokriging of regionalized compositional data using four different methods. Case study: bauxites in Hungary Spain: Universitat Politècnica de Catalunya (UPC), 2002. 6p.
- DELGADO, R. T., MULLER, U., VAN DEN BOOGAART, K. G., WARD, C. Block cokriging of a whole composition. In: Proceedings of APCOM 2013, Porto Alegre, Brazil, November 2013. p. 267-277.
- DEUTSCH, C. V., JOURNEL, A. G. GSLIB: Geostatistical sofware library and user's guide New York: Oxford University Press, 1998. 369p.
- EGOZCUE, J. J., PAWLOWSKY-GLAHN, V. Groups of parts and their balances in compositional data analysis Spain: Technical University of Catalonia, 2005. 34p.
- EGOZCUE, J.J., PAWLOWSKY-GLAHN, V., MATEU-FIGUERAS, G., BARCELÓ-VIDAL, C. Isometric logratio transformations for compositional data analysis. Mathematical Geology, v. 35, n. 3. p. 279-300, 2003.
- ISAAKS, E. H., SRIVASTAVA, M. R. An introduction to applied geostatistics New York: Oxford University Press, 1989. 561p.
- LARK, R. M., BISHOP, T. F. A. Cokriging particle size fractions of the soil. European Journal of Soil Science, v. 58, p. 763-774, 2007.
- MARECHAL, A. Cokrigeage et regression en correlation intrinsique France, Fontainebleau: Centre de Geostatistique de Fontainebleau, 1970. 40p.
- MATHERON, G. Principles of geostatistics. Economic Geology,v. 58, p. 1246-1266, 1963.
- MATHERON, G. The intrinsic random functions and their applications. Advance Applied Probability, v. 5, p. 439-468, 1973.
- ODEH, I. O. A., TODD, A. J., TRIANTAFILIS, J. Spatial prediction of soil particle-size fractions as compositional data. Soil Science, v. 168, p. 501-515, 2003.
- PAWLOWSKY-GLAHN, V., BUCCIANTI, A. Compositional data analysis - theory and applications Chichester: Wiley, 2011. 241p.
- PAWLOWSKY-GLAHN, V., OLEA, R. A. Geostatistical analysis of compositional data New York: Oxford University Press, 2004. 181p.
- PAWLOWSKY-GLAHN, V., EGOZCUE, J. J., TOLOSANA, D. R. Lecture notes on compositional data analysis Spain: Technical University of Catalonia, 2010. 108p.
- PAWLOWSKY-GLAHN, V. Cokriging of regionalized compositions. Mathematical Geology, v. 21, p. 513-521, 1989.
- PAWLOWSKY-GLAHN, V., OLEA, R., DAVIS, J. C. Estimation of regionalized compositions: a comparison of three methods. Mathematical Geology, v. 27, p. 105-127, 1995.
- PEARSON, K. Mathematical contributions to the theory of evolution - on a form of spurious correlation which may arise when indices are used in the measure of organs. Proceedings of the Royal Society of London, v. 60, p. 489-502, 1897.
- SRIVASTAVA, R. M. A non-ergodic framework for variogram and covariance functions Stanford, California: Stanford University, 1987. 122p. (Master's Thesis).
- WARD, C., MULLER, U. Multivariate estimation using log ratios: a worked alternative. In: ABRAHAMSEN, P., HAUGE, R., KOLBJØRNSEN, O. (Eds.). Geostatistics Oslo 2012Springer, Dordrecht, p. 333-343, 2012.
Publication Dates
-
Publication in this collection
Apr-Jun 2016
History
-
Received
11 Mar 2015 -
Accepted
26 Mar 2016

 A Geostatistical Framework for Estimating Compositional Data Avoiding Bias in Back-transformation
A Geostatistical Framework for Estimating Compositional Data Avoiding Bias in Back-transformation