Abstract
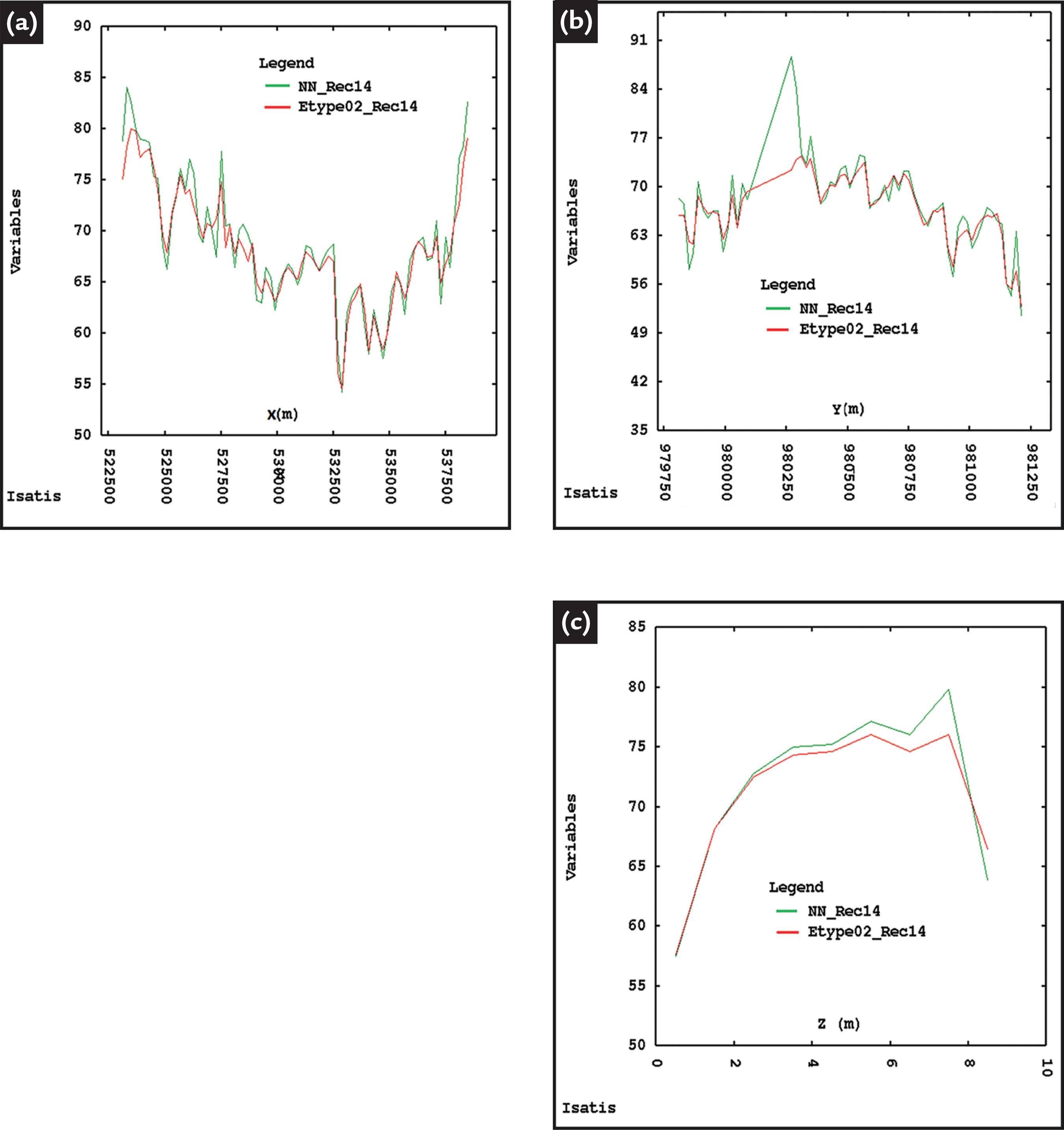
Estimation of some mineral deposits involves chemical species or a granulometric mass balance that constitute a closed constant sum (e.g., 100%). Data that add up to a constant are known as compositional data (CODA). Classical geostatistical estimation methods (e.g., kriging) are not satisfactory when CODA are used, since bias is expected when estimated mean block values are back-transformed to the original space. CODA methods use nonlinear transformations, and when the transformed data are interpolated, they cannot be returned directly to the space of the original data. If these averages are back-transformed using the inverse function, bias is generated. To avoid this bias, this article proposes geostatistical simulation of the isometric logratio ratio (ilr) transformations back-transforming point simulated values (instead of block estimations), with the averaging being postponed to the end of the process. The results show that, in addition to maintaining the mass balance and the correlations among the variables, the means (E-types) of the simulations satisfactorily reproduce the statistical characteristics of the grades without any sort of bias. A complete case study of a major bauxite deposit illustrates the methodology.
Keywords:
compositional data; isometric transformations ratios (ilr); simulation; closure