Abstract
Some mineral deposits show mineralization along layers. These layers may pass through several subsequent geological events such as folding and/or severe erosional processes. Grades within these deposits tend to be correlated along orientations where the mineralization was originally deposited or along the same geological period (stratigraphic level). Consequently, some locations close to each other in terms of geographical coordinates can show uncorrelated grades. Spatial continuity analysis can also be affected by error inflicted by combining samples from different stratigraphic levels. This article uses the coordinate transformation (unfolding) to align the grades measured along the same stratigraphic level. The modification in coordinates improved the spatial continuity modeling and the grade estimates at non-sampled locations. The results showed that the mean of the relative error between the estimated value and the real value of the samples using unfolding is -0.10%. However, when using the original coordinates, the mean of the relative error is -0.65%. Furthermore, the correlation between the real and estimated value using crossvalidation is greater using stratigraphic coordinates. A complete case study in a manganese deposit illustrates the methodology.
Keywords:
Change of coordinates; stratigraphic coordinates; grade estimation; kriging
1. Inroduction
Mineral deposits such as bauxite, coal, manganese and some nickel laterites are constituted mainly by large mineralized layers. These layers formed by sedimentation or weathering processes may pass through several subsequent geological events such as folding, erosions and/or basin formation.
One of the most common problems for this kind of deposit is the spatial continuity analysis. This spatial continuity may be affected by an error caused by the combination of samples from different stratigraphic levels. For example, two samples may be in the same topographic or Cartesian level but along a different geologic or stratigraphic horizon. Figure 1 (a) shows that the Cartesian coordinates of samples 1 and 4 are at the top and at the bottom of the mineralized layer respectively, however at the same z – topographic coordinate. The analysis of the spatial continuity and the block estimates would benefit if samples deposited along the same geologic horizon were used; therefore, Sample 1 should have more spatial connectivity with Sample 2 than with Sample 4 (see Figure 1b).
Interpretation of coordinates between different samples, (a) Cartesian coordinates (b) stratigraphic coordinates.
The geostatistical modeling is based on the spatial dependence of the samples. In this type of strata-bound deposit, it means locations that were deposited during the same period of time are spatially linked (Koppe, 2005KOPPE, V. C. Análise de incerteza associada à determinação da velocidade de onda sônica em depósitos de carvão obtida por perfilagem geofísica. Porto Alegre: Universidade Federal Rio Grande do Sul, 2005. 282p.). Deposits submitted to folding after the mineralization took place can be affected in spatial continuity analysis and consequently in the estimates. One of the ways to minimize this effect is by transforming the vertical coordinates (McArthur, 1988MCARTHUR, G. J. Using geology to control geostatistics in the Hellyer deposit. Mathematical Geology, v. 20, n. 4, p. 343-366, 1988.; Deutsch, 2002DEUTSCH, C. V. Geostatistical reservoir modeling. New York: Oxford University Press,, 2002. 376p.). The coordinate transformation (unfolding) is used to align the grades measured along stratigraphic levels (or geochemical level depending on the case) to improve the analysis of the spatial continuity of the attributes and better estimate block values, using a reference surface (the hangwall or the footwall), taking into consideration the geological characteristics of the unit.
The objective of this paper is to evaluate the possible benefits in terms of increasing the precision and accuracy of the estimates with the change of coordinates. A manganese deposit is used to illustrate the methodology.
2. Methodology
In the 80s and 90s, some authors demonstrated interest in using stratigraphic coordinates (Rendu and Readdy, 1982RENDU, J. M., READDY, L. Geology and the Semivariogram. A Critical Relationship. In: APCOM SYMPOSIUM, 17. New York: A.I.M.E., 1992, p. 771-783.; Weber, 1982WEBER, K. J. Influence of common sedimentary structures on fluid flow in reservoirs models. Journal of Petroleum Technology, v. 34, p. 665-672, 1982.-1990WEBER, K. J., VAN GEUNS, L. C. Framework for constructing clastic reservoir simulation models. Journal of Petroleum Technology, v. 42, n. 10, p. 1248-1253, 1990.; Dagbert et al., 1984DAGBERT, M., DAVID, M., CROZEL, D., DESBARATS, A. Computing variograms in folded strata-controlled deposits. In: VERLY, G. et al. (Ed.). Geostatisitcs for Natural Resources Characterization. D. Reidel, Dordrecht., p. 71-89. 1984. (Part 1).; Bashore and Araktingi, 1994BASHORE, W. M., ARAKTINGI, U.G. Importance of a geological framework and seismic data integration for reservoir modeling and subsequent fluid-flow. In: COBURN, T.C., YARUS, J. M., CHAMBERS, R. L.(Ed.). Stochastic modeling and geostatistics: principles, methods and case studies. AAPG Computer Applications in Geology, n. 5, p. 159-176, 1994.). McArthur (1988)MCARTHUR, G. J. Using geology to control geostatistics in the Hellyer deposit. Mathematical Geology, v. 20, n. 4, p. 343-366, 1988. used the transformation of Cartesian coordinates into stratigraphic coordinates in a uranium deposit in Australia, assigning arbitrarily stratigraphic numbers to the new vertical coordinate Z. Since then, a few studies have shown the process systematically to transform Cartesian coordinates into stratigraphic coordinates in a real case study; among them we find a real case of sonic wave slowness in Koppe et al., (2006)KOPPE, C. V., COSTA, J. F., KOPPE, J. C. Coordenadas cartesianas x coordenadas geológicas em geoestatística: aplicação à variável vagarosidade obtida por perfilagem acústica. REM - Revista Escola de Minas, v. 59, n. 1, p. 25-30, 2006.. Other alternatives to the unfolding techniques can be considered such as geostatistics with locally varying Anisotropy (Boisvert et al., 2009BOISVERT, J., MANCHUK, J., DEUTSCH, C V. Kriging and simulation in the presence of locally varying anisotropy. Mathematical Geosciences, v. 41, n. 10, p. 585-601. 2009.).
Deutsch (2002)DEUTSCH, C. V. Geostatistical reservoir modeling. New York: Oxford University Press,, 2002. 376p. suggests some approximations that can be made to transform Cartesian coordinates into stratigraphic coordinates. A vertical coordinate will be defined as the relative distance between a correlation top and correlation base grid. This will make it possible to infer natural measures of horizontal correlation and to preserve the geologic structure in the final numerical model (Deutsch, 2002DEUTSCH, C. V. Geostatistical reservoir modeling. New York: Oxford University Press,, 2002. 376p.). The new vertical coordinates can be calculated using the following equation:
where:
Z(i)str = Z elevation after stratigraphic correction in sample (i);
Z(i) = actual Z elevation in sample (i);
Z(i)b = bottom layer Z elevation in sample (i);
Z(i) t = top layer Z elevation in sample (i);
T = average layer thickness;
n = number of samples.
This article considered that the mineralized layer has slight changes in thickness along its extension (i.e. Z(i)t-Z(i)b ≅ T), therefore, the equation suggested by Deutsch (2002) has been redefined as follows:
Equations 2 and 3 represent the stratigraphic coordinates performed using as references the footwall and hangwall distance correction respectively. The new vertical coordinate transformations will be a plane shape, maintaining the distances between horizontal coordinates (Cartesian coordinates).
This transformation, does not correct the horizontal distances between samples, which can, in cases where the layers are folded strongly, modify the horizontal continuity determined by the samples values, leading to errors in the determination of the variograms. Therefore, the use of this transformation is appropriate for deposits that show only a slight folding along of the layers. Figure 2 shows the transformation of a stratiform geological layer whose coordinates on the vertical axis (Figure 2a) are transformed to stratigraphic coordinates corrected by the footwall (Figure 2b) or hangwall (Figure 2c) of the layer.
Example of a stratiform layer, (a) Cartesian geological, (b) stratigraphic coordinates corrected by the footwall of the layer, (c) stratigraphic coordinates corrected by the hangwall of the layer. The change of coordinates is made only on the vertical axis (Z).
Figure 3 shows the spatial distribution of the original data in the plane YZ. Note that, the stratiform geological layer has a slight folding along the deposit.
This article begins with a comparison between two point estimates (footwall and hangwall) to choose which reference surface is the most adequate. Subsequently, we will analyze the spatial continuity and point estimates between original Cartesian coordinates and stratigraphic coordinates. Finally, we will make an estimate in blocks to validate the results of the proposed methodology.
3. Results
3.1 Case Study
The case study corresponds to a data set from a manganese deposit located in the Brazilian Amazon (Figure 4).
3.2 Selection of the Surface of Reference
In order to evaluate the two corrections and choose the one that will be used in the analysis of spatial continuity and estimation, two datasets with a new vertical coordinate along Z (distance to hangwall or footwall) were created. Cross-validation (Isaaks and Srivastava, 1989ISAAKS, E. H., SRIVASTAVA, M. R. An introduction to applied geostatistics. New York: Oxford University Press,, 1989. 561p.) was used to check the quality of the estimates for the two coordinate-transformed datasets. Figure 5 (a) shows that the mean error of the variable manganese (mn1) corrected by the hangwall is closer to zero (-0.12) compared with the mean error of the same variable (Figure 5 (b)) corrected by the footwall (-0.55). Furthermore, the spread around the mean error was lower using the hangwall. Consequently, it was decided to proceed with the stratigraphic coordinates corrected by the hangwall.
Histogram of distribution of error, (a) coordinates correct by the hangwall, (b) coordinates corrected by the footwall.
Due to the difference in the sample support (variables analyzed in different granulometric fractions), it was necessary to proceed with an auxiliary (accumulated) variable of the manganese. At the end of the estimation process, the accumulation is divided by the mass fraction at each block to return unbiased grade estimates (Marques et al., 2014MARQUES, D. M., HUNDELSHAUSSEN, R. J., COSTA, J. F., APPARICIO, E. M. The effect of accumulation in 2D estimates in phosphatic ore. REM - Revista Escola de Minas, v. 67, n. 4, p. 431-437, 2014.). Furthermore, the jackknife cross validation was performed.
3.3 Spatial Continuity Analysis
The spatial continuity for the manganese was obtained using experimental non ergodic correlograms (Srivastava, 1987SRIVASTAVA, R. M. Non-ergodic framework for variogram and covariance functions. Stanford, CA: Stanford University, 1987. (Master's Thesis).). The construction of these models was performed using data at the original Cartesian coordinates as well as at the stratigraphic coordinates. Figure 6 shows the models adjusted to the major horizontal directions of anisotropy for each data coordinate. Note that, the modeling using stratigraphic coordinates (Figure 6c, d) produces better structured experimental correlograms than when using Cartesian coordinates (Figure 6a, b). The noise noted in the experimental correlogram using Cartesian coordinates (Figure 6a, b) is due to the influence of events subsequent to the formation of the deposit.
Models of spatial continuity using Cartesian coordinates (a) major axis N-90 dip 0 (b) intermediate axis N-0 dip 0 and, using stratigraphic coordinates (c) major axis N-90 dip 0 (d) intermediate axis N-0 dip 0.
When mixing samples from different stratigraphic levels, the grades lose spatial connectivity, since they are a result of a sampling mix that was probably not deposited along the same deposition period (different horizons). This leads to bias and noise when calculating the experimental spatial continuity and ultimately leading to incorrect spatial continuity.
3.4 Validation of Estimates points Using Original Coordinates and Stratigraphic Coordinates
A comparison was made using cross validation (Isaaks and Srivastava, 1989ISAAKS, E. H., SRIVASTAVA, M. R. An introduction to applied geostatistics. New York: Oxford University Press,, 1989. 561p.) to check the results by the coordinate transformation and using the originals. The method consists of removing momentarily a sample positioned at the location (u) from the original dataset. This location (u) is estimated using the information of the remaining samples and, finally, the difference between the estimated value and the actual value at the same location (u) is calculated. This difference is known as the error of cross validation. The process is repeated for all samples in the dataset.
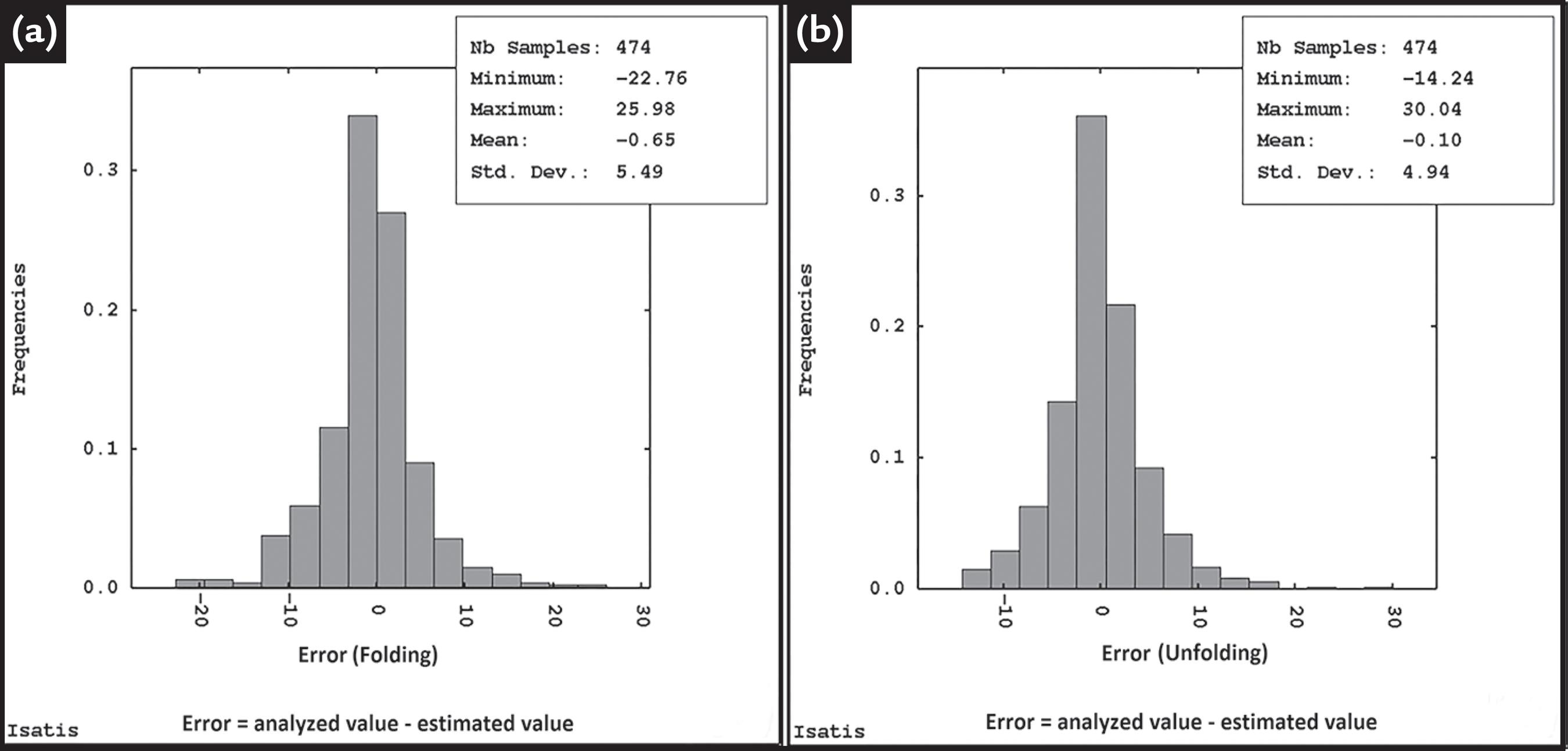
Figures 7a and 7b show the error histogram for the estimates using both the Cartesian coordinates and the stratigraphic coordinates. Note that the mean error using stratigraphic coordinates (Figure 7b) is close to zero (-0.10) whilst the mean error using Cartesian coordinates is -0.65 (Figure 7a). Furthermore, the spread of the error around the center is smaller when using stratigraphic coordinates.
Error histograms obtained by cross validation using (a) original Cartesian coordinates and (b) stratigraphic coordinates correction.
Likewise, Figures 8a and 8b show the scatterplot between the two estimates (original vs. unfolding). Note that the correlation between real and estimated value using stratigraphic coordinates (Figure 8b) is 0.50 whilst the correlation between real and estimated value using Cartesian coordinates is 0.45 (Figure 8b). Globally this difference may be insignificant, but we can see that the dispersion of the estimated values in relation to real value using unfolding (Figure 8b) is much less than the estimated values estimated in the Cartesian coordinates (Figure 8a). For example, the estimated values in red are closer when using stratigraphic coordinates (Figure 8b) than when using Cartesian coordinates (Figure 8a).
Correlations obtained by cross validation using (a) original Cartesian coordinates and (b) stratigraphic coordinates correction.
3.5. Validation of Estimates Blocks Using Stratigraphic Coordinates
The first check used to verify the models is the reproduction of the global declustered mean of the original data. Figure 9 shows the histogram of declustered data (Figure 9a) obtained using the polygonal method (Isaaks and Srivastava, 1989) and histogram of the estimated data (Figure 9b) obtained by ordinary kriging (Matheron, 1963MATHERON, G. Principles of geostatistics. Economic Geology, n. 58, p. 1246-1266, 1963.). Note that the global mean of the estimates (47.19%) is very similar to the declustered mean (47.15%), with a slight relative difference of 0.08% between the two, thus ensuring a good reproduction by the estimated model.
Validation of global mean, (a) declustered data histogram (b) block model grades histogram using the stratigraphic coordinates.
Next, the local means were checked. Basically, this method consists in locally comparing the values of the declustered mean and the kriged block model for each attribute along bands in the X, Y and Z directions. The result of each mean is plotted versus its location along X, Y and Z. The plots of the local mean show coherence between both estimates along each band. Figures 10 (a, b, c) show the swath plots between the estimated blocks and declustered data along the three main directions, i.e. X, Y, and Z. Note that the local mean estimates are very similar to the declustered mean along each band. The bands used were 100 m wide along X and Y and 8 m along Z.
Swath plot for the manganese, (a) X direction, (b) Y direction and (c) Z. Red line represents the declustered mean from the data and black line represents the estimated blocks.
4. Conclusion
Stratiform deposits are frequently found in different mineral commodities, and they are properly modelled and estimated in most cases. Coordinate correction along the vertical axis (Z) using stratigraphic coordinates is essential in geostatistical estimations for this style of mineralization. Ignoring this practice leads to a mix between samples from different geochemical horizons possibly not correlated and ultimately leading to a significant bias in the estimates.
The use of stratigraphic coordinates showed to be more appropriate for properly capturing the spatial continuity. Correlograms were more continuous with greater adhesion between the experimental points and the model, if compared to the ones using Cartesian coordinates. Furthermore, the error derived by comparing the estimated values and the actual values was more precise and accurate when using stratigraphic coordinates than when using Cartesian coordinates. Moreover, the correlation between the real and estimated value using cross-validation is greater using stratigraphic coordinates.
The global and local means in the estimated grade block model using stratigraphic coordinates is very similar to the global and local means using declustered data.
References
- BASHORE, W. M., ARAKTINGI, U.G. Importance of a geological framework and seismic data integration for reservoir modeling and subsequent fluid-flow. In: COBURN, T.C., YARUS, J. M., CHAMBERS, R. L.(Ed.). Stochastic modeling and geostatistics: principles, methods and case studies. AAPG Computer Applications in Geology, n. 5, p. 159-176, 1994.
- BOISVERT, J., MANCHUK, J., DEUTSCH, C V. Kriging and simulation in the presence of locally varying anisotropy. Mathematical Geosciences, v. 41, n. 10, p. 585-601. 2009.
- DAGBERT, M., DAVID, M., CROZEL, D., DESBARATS, A. Computing variograms in folded strata-controlled deposits. In: VERLY, G. et al. (Ed.). Geostatisitcs for Natural Resources Characterization D. Reidel, Dordrecht., p. 71-89. 1984. (Part 1).
- DEUTSCH, C. V. Geostatistical reservoir modeling New York: Oxford University Press,, 2002. 376p.
- ISAAKS, E. H., SRIVASTAVA, M. R. An introduction to applied geostatistics New York: Oxford University Press,, 1989. 561p.
- KOPPE, V. C. Análise de incerteza associada à determinação da velocidade de onda sônica em depósitos de carvão obtida por perfilagem geofísica Porto Alegre: Universidade Federal Rio Grande do Sul, 2005. 282p.
- KOPPE, C. V., COSTA, J. F., KOPPE, J. C. Coordenadas cartesianas x coordenadas geológicas em geoestatística: aplicação à variável vagarosidade obtida por perfilagem acústica. REM - Revista Escola de Minas, v. 59, n. 1, p. 25-30, 2006.
- MATHERON, G. Principles of geostatistics. Economic Geology, n. 58, p. 1246-1266, 1963.
- MCARTHUR, G. J. Using geology to control geostatistics in the Hellyer deposit. Mathematical Geology, v. 20, n. 4, p. 343-366, 1988.
- MARQUES, D. M., HUNDELSHAUSSEN, R. J., COSTA, J. F., APPARICIO, E. M. The effect of accumulation in 2D estimates in phosphatic ore. REM - Revista Escola de Minas, v. 67, n. 4, p. 431-437, 2014.
- RENDU, J. M., READDY, L. Geology and the Semivariogram. A Critical Relationship. In: APCOM SYMPOSIUM, 17. New York: A.I.M.E., 1992, p. 771-783.
- SRIVASTAVA, R. M. Non-ergodic framework for variogram and covariance functions Stanford, CA: Stanford University, 1987. (Master's Thesis).
- WEBER, K. J. Influence of common sedimentary structures on fluid flow in reservoirs models. Journal of Petroleum Technology, v. 34, p. 665-672, 1982.
- WEBER, K. J., VAN GEUNS, L. C. Framework for constructing clastic reservoir simulation models. Journal of Petroleum Technology, v. 42, n. 10, p. 1248-1253, 1990.
Publication Dates
-
Publication in this collection
Oct-Dec 2015
History
-
Received
08 Apr 2015 -
Accepted
02 Sept 2015