Abstract
A common technique in hard rock tunneling, and underground excavation in general, is drilling and blasting. This method of excavation assumes that damage will be done to the surrounding rock mass depending on its quality. Herein is a proposal for how to estimate blast-damaged zone extent and shape, and how to quantify rock mass properties in this zone. Comparison was made, using FEM, between models with and without blast-damaged zone consideration through analyzing its impact on the support load. Results showed greater support loads in the case of blast-damaged zone modeling. Also, comparison was made between the proposed method for blastdamaged zone quantification and quantification using blast damage factor D. Results showed that in both cases, the support loads are in same magnitude order. In other words, compared to the blast damage factor D method, the proposed is more objective and makes it possible to describe the blasting process before it is actually done.
Keywords:
Tunneling in hard rock; rock blasting; blast-damaged zone; rock breakage by explosives
1. Introduction
Tunneling in hard rock is hard to imagine without using explosives for rock excavation. In the case of this excavation method, the surrounding rock mass that represents the tunnel walls is damaged by blasting. Depending on how well the blasting pattern is designed, determines how damaged the surrounding rock mass will be. Many researches have been conducted to describe and quantify blast-induced damage of surrounding rock mass and many techniques have been invented to prevent this damage. Many tests were conducted by Swedish Rock Engineering Research Organization (SveBeFo) and these test offered new explanations on how rock breakage by explosives occurs Langefors and Kihlstrom (1973)LANGEFORS, U., KIHLSTROM, B. The modern techniques of rock blasting. New York: John Wiley and Sons, 1973. and Brinkmann (1987BRINKMANN, J. R. Separating shock wave and gas expansion breakage mechanisms. PROC.2ND INT. SYMP. ON FRAGMENTATION BY BLASTING. Keytone, Colorado USA: 1987. p. 6-15., 1990)BRINKMANN, J. R. An experimental study of the effects of shock and gas penetration in blasting. PROC. 3RD INT. SYMP.ON FRAGMENTATION BY BLASTING, Brisbane, Australia: 1990. p. 55-66.. Järnvägs (1996)JÄRNVÄGS, A. M. A. Swedish National Railway Authorities Complement to AMA 83. Rock Technique Rpt. TM-95-060 1996-09-01. Banverket, Borlänge, 1996. introduced a contour blasting technique that reduced blasting damage to surrounding rock mass. Ouchterlony (1997)OUCHTERLONY, F. Prediction of crack lengths in rock after cautious blasting with zero inter-hole delay. Int. J. for Blasting and Fragmentation, n. 1, p. 417-444, 1997. gave an equation for estimating radial crack length, and later this equation was expanded by correction factors, Ouchterlony et al. (2002)OUCHTERLONY, F., OLSSON, M., BERGQVIST, I. Towards new Swedish recommendations for cautious perimeter blasting. Fragblast, v. 6, n. 2, p. 235-261, 2002.. Many papers that consider damaged zone extent were published by Hustrulid. Hustrulid (1999) analyzed the energy and work done by an explosive charge in a borehole. In 2002. Hustrulid and Lu presented their approach to determine peak particle velocity (PPV), which was later revised by Hustrulid and Johnson (2008)HUSTRULID, W., JOHNSON, J. A gas pressure-based drift round blast design methodology. In: SCHUNNESSON, H. NORRDLUND, E. Proceedings, MassMin 2008. Lulea, p. 567-669, June 9-11, 2008.. Hustrulid (2010)HUSTRULID, W. Some comments regarding development drifting practices with special emphasis on caving applications. PROC. CAVING 2010 SYMP. In: POTVIN, AGG. On Block and Sublevel Caving. Perth Australia. p. 3-44, 2010. used Ash's (1963)ASH, R. L. The mechanics of rock breakage. Pit and Quarry I, (Aug) p. 98-112. Part , II (Sept) p. 118-123. Part III, (Oct), p. 126-131. Part IV (Nov), p. 109-118, 1963. a classic approach to develop the extent of damage based on explosive energy. Based on Holmberg's (1982)HOLMBERG, R. Charge calculation for tunnelling. In: HUSTRULID W.A. (Ed.), Underground Mining Methods Handbook, Soc. Min. Metall. Explosives, p.1580-1589, 1982. paper, Hustrulid (2010)HUSTRULID, W. Some comments regarding development drifting practices with special emphasis on caving applications. PROC. CAVING 2010 SYMP. In: POTVIN, AGG. On Block and Sublevel Caving. Perth Australia. p. 3-44, 2010. presented the Rock Constant Approach. Senuk (1979)SENUK, V. M. The impulse from an explosion and conditions for its greater utilization in crushing hard rock masses in blasting.: Soviet Mining Science p. 22-27, 1979. presented his method for crack zone radius estimation. This method was based on the relationship between borehole pressure and tensile strength. Kanchibotla et al. (1999)KANCHIBOLTA S. S., VALERY, W., Morrell, S. Modeling fines in blast fragmentation and its impact on crushing and grinding. Proc. of Explo. '99-A CONFERENCE ON ROCK BREAKING. Brisbane, Australia: The Australasian Institute of Mining and Metallurgy, p. 137-144, 1999. offered an equation to estimate the crushing zone radius based on the relationship between borehole radius, borehole pressure and compressive strength of rock. Most of models cited here use parameters such as PPV, borehole radius and pressure inside borehole, and strength parameters usually consider only compressive strength of rock, although it is very well known that failure in rock occurs by tension or shear. Tensile strength of rock was incorporated in the theoretical work published by Drukovanyi et al. (1976), although this work does not explain mechanisms by which blast damage in rock occurs. Also, practice showed that this approach was applicable only for rocks with a compressive strength over 100 MPa. These models are only considered for estimating the extent of the blast damaged zone and do not provide any suggestion as to how to estimate the mechanical properties of rock mass in this zone.
Kwon et al. (2009)KWON, S., LEE, C.S., CHO, S.J., JEON, S.W., CHO, W.J. An investigation of the excavation damaged zone at the KAERI underground research tunnel. Tunnelling and underground space technology, n. 24, p. 1-13, 2009. conducted a series of tests to determine the extent and properties of the blast damaged zone at the KAERI underground research tunnel. It is reported that the blast-damaged zone (BDZ) had an extent of around 2 m; the RQD in this zone decreased around 17% in comparison with the RQD in undisturbed rock mass; and the elastic module decreased around 56%. A decreased RQD value means that the rock mass in the damaged area is becoming more jointed, which is an important fact for this paper.
A description of rock damage by blasting was incorporated in Hoek-Brown's failure criterion by introducing the blast damage factor D, Hoek et al (2002)HOEK, E., CARRANZA-TORRES, C. Corkum, B., Hoek-Brown criterion - 2002 edition. Proc. NARMS-TAC CONFERENCE. Toronto: 2002, v. 1, p. 267-273.. Factor D at first was used for estimating parameters of Hoek-Brown's failure criterion mb, s and a. Later on, it was incorporated in the estimation of a rock mass modulus Hoek and Diederichs (2006)HOEK, E, DIEDERICHS, M.S. Empirical estimation of rock mass modulus. International Journal of Rock Mechanics and Mining Sciences, n. 43, p. 203-215, 2006.. Values for the blast damage factor and extent of damaged zone are suggested by Hoek (2002HOEK, E., CARRANZA-TORRES, C. Corkum, B., Hoek-Brown criterion - 2002 edition. Proc. NARMS-TAC CONFERENCE. Toronto: 2002, v. 1, p. 267-273., 2012)HOEK E. Blast damage factor D. Technical note for RocNews, 2012.. This suggestion is made on empirical investigations and there is no solution for the exact estimation of these parameters. A common mistake made by engineers is that factor D is applied on whole rock mass instead of just the close perimeter around excavation. This mistake is caused by lack of exact methods to estimate the damage zone extent and to estimate the mechanical properties of this zone. With this in mind, the authors herein has now mainly focused on this problem, and presents a method for estimating the extent and rock mass properties of the blast-damaged zone around the excavation.
2. Rock blasting theory
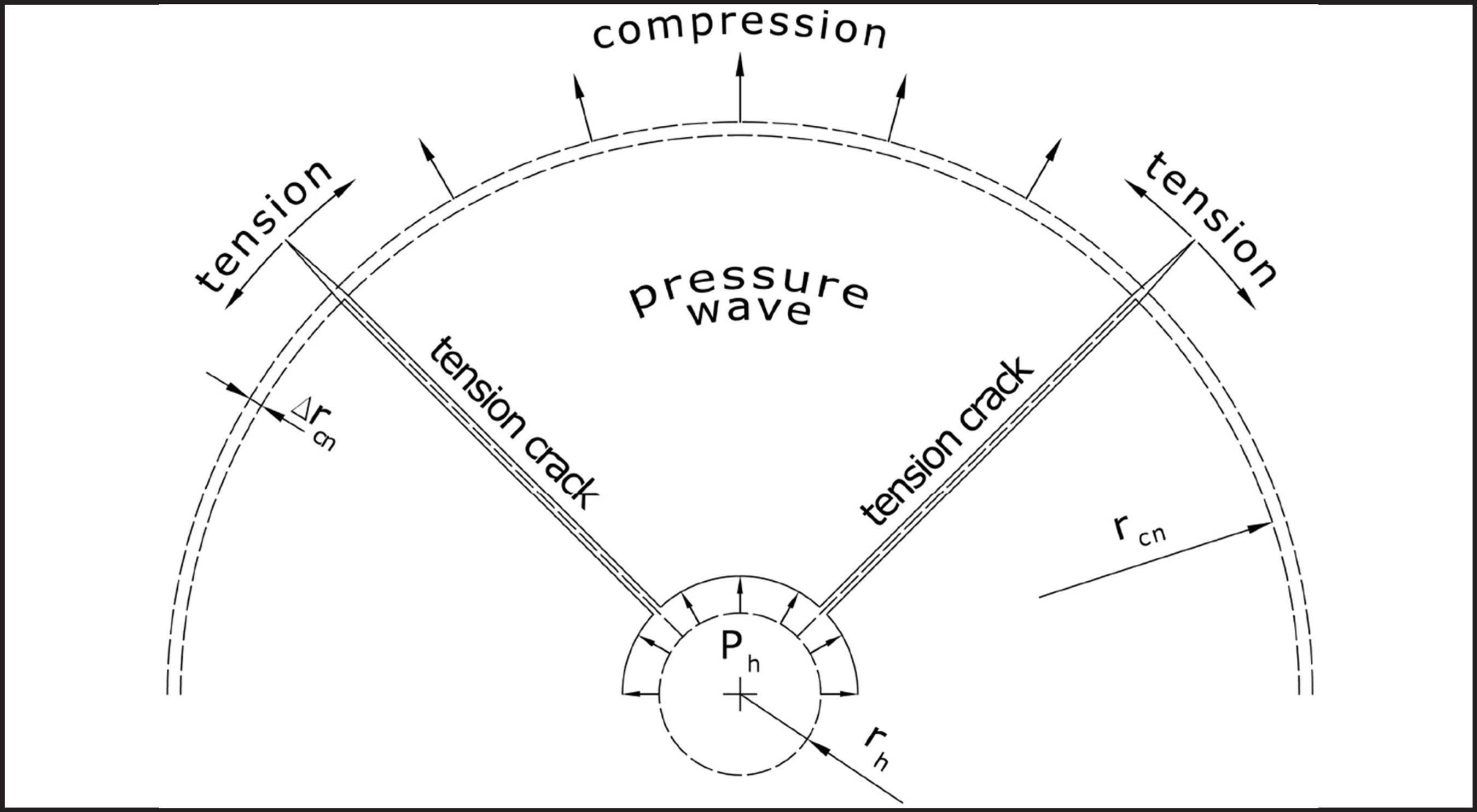
According to a new rock blasting theory, Torbica and Lapcevic (2014)TORBICA, S., LAPCEVIC, V. Rock breakage by explosives. European International Journal of Science and Technology, p. 96-104, 2014., it is possible to calculate the radii of zones having a different density of radial cracks around the blasthole. This theory explains the fracturing mechanism of rock under explosive load. Here, the main part of that theory is presented, since it is the basis of this paper. Detonation of an explosive charge in rock results in dynamic loading of the walls of the borehole and generation of a pressure wave that transmits energy through the surrounding medium.
The pressure wave extends from borehole walls circularly around the borehole (Figure 1). At the distance rcn from the borehole compressive stress of the rock in the radial direction is:
Where:
σrc- radial compressive stress
Ph - borehole pressure
rh - borehole radius
rcn - crack zone radius
On the other hand:
Where:
M - pressure wave modulus
er - radial strain
E -Young's modulus of rock
ν - Poisson's ratio
Or:
Therefore:
At the distance rcn, before the pressure wave gets to it, the perimeter of the closed circular ring zone of rock mass is:
When the pressure wave reaches the closed circular ring zone of rock mass, it is moved to a new position with a radius (rcn + ∆rcn), and with the perimeter:
Therefore:
Once the closed circular ring zone of rock mass is subjected to tension with a lateral strain:
For the formation of the radial tension cracks, tensile strain is required:
Where:
et - tensile strain
σt - tensile strength
E - Young's modulus of rock
In addition, the number (n) of radial tensile cracks formed at a distance rcn will be:
Therefore, it is:
Therefore:
Therefore, for the borehole radius rh =0.051m and the borehole pressure Ph=1.6 GPa in limestone with tensile strength σt=7MPa, Poisson's ratio ν=0.3 (Table 1) will be:
In Figure 2, the schematic illustration of tension crack length and density around blasthole is shown. Practical application of this theory was demonstrated by Torbica and Lapcevic (2014)TORBICA, S., LAPCEVIC, V. Rock breakage by explosives. European International Journal of Science and Technology, p. 96-104, 2014. for the estimation of blasted rock fragmentation.
3. Estimating the extent and properties of the blast-damaged zone around the underground excavation
3.1 Damaged zone extent and shape
The extent and shape of the damaged zone around the excavation depends on the blasting pattern, cross section of the excavation and the structure of rock mass (primary block sizes). One should imagine rock mass as a set of interlocked monolith blocks that are separated by preexisting rock joints. In this manner rock blocks may be considered to be an elastic part of rock mass and their plasticization is done through the blasting process when blast-induced radial cracks are formed. It is well known that discontinuities as joints and fractures in rock mass limit pressure wave propagation and therefore may limit propagation of radial cracks induced by explosive charge, Figure 3. This also means that preexisting joints and fractures define the extent and shape of the blast damaged zone around the excavation, as explosive charge will break only the rock block in which it is placed. In other words, preexisting joints define domain for pressure wave propagation. Numerical investigations, using distinct element modeling, on radial crack and pressure wave propagation in jointed rock mass are presented by Aliabadian et al. (2014)ALIABADIAN, Z., SHARAFISAFA, M., MORTAZAVI, A., MAAREFVAND, P. Wave and fracture propagation in continuum and faulted rock masses: distinct element modeling. Arabian Journal of Geosciences. p. 5021-5035, 2014. DOI 10.1007/s12517-013-1155-3.
https://doi.org/10.1007/s12517-013-1155-...
.
Impact of preexisting joints in rock mass on blast induced radial crack length, published in Saiang (2008) with permission from Mats Olsson.
As it is possible to determine the radii of cracking zones around the blasthole, we can use this principle to determine the extent of the damaged zone in the rock mass surrounding the excavation. As first, the damaged zone extent depends on the explosive pressure in the contour blastholes. It is well known that contour blastholes are placed closer and charged with less explosive than other blastholes in the blasting pattern. Therefore, if blastholes are charged less, the length of the tension cracks around the excavation decreases and vice versa. The shape of the damaged zone depends on the excavation cross section and its shape is the same as the shape of excavation cross section, but it is offset for the radius of the damaged zone.
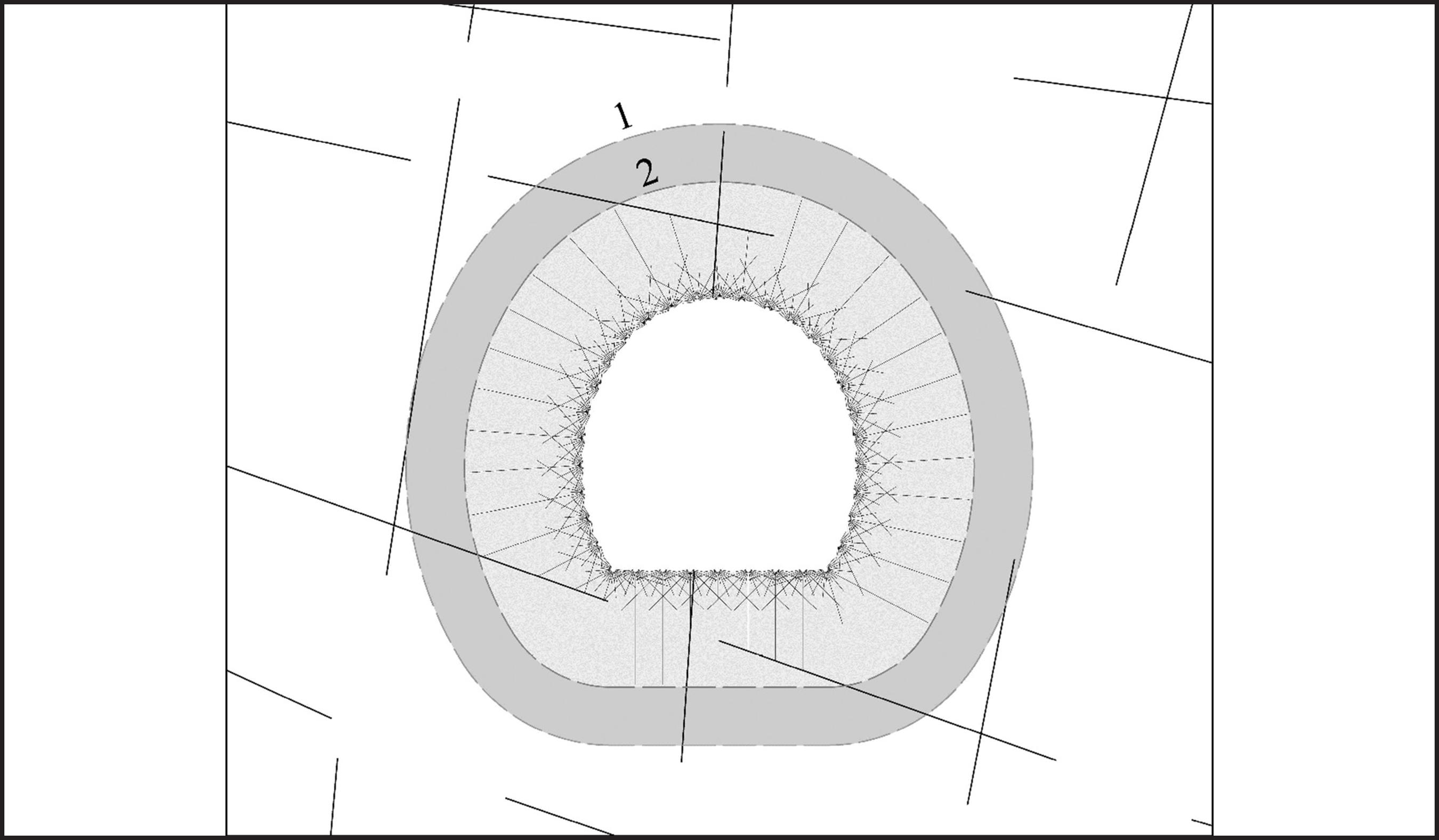
Depending on how much rock mass is jointed we can differ two possible situations. The first situation is when primary block size is larger than the maximum length of the blast induced radial cracks in zone r4. In this case pressure wave that induces radial cracks is not limited by preexisting joints in rock mass and radial cracks may reach their maximum length, Figure 4. Therefore, for this situation, the extent of the blast damaged zone is equal to the maximum length of the radial cracks in cracking zone r4.
Blasting in rock mass where primary block sizes are larger than the maximum length of the blast induced radial cracks. Line 1 marks maximum length from contour blastholes to preexisting rock joints. Line 2 marks maximum length of blast induced radial cracks in monolith block.
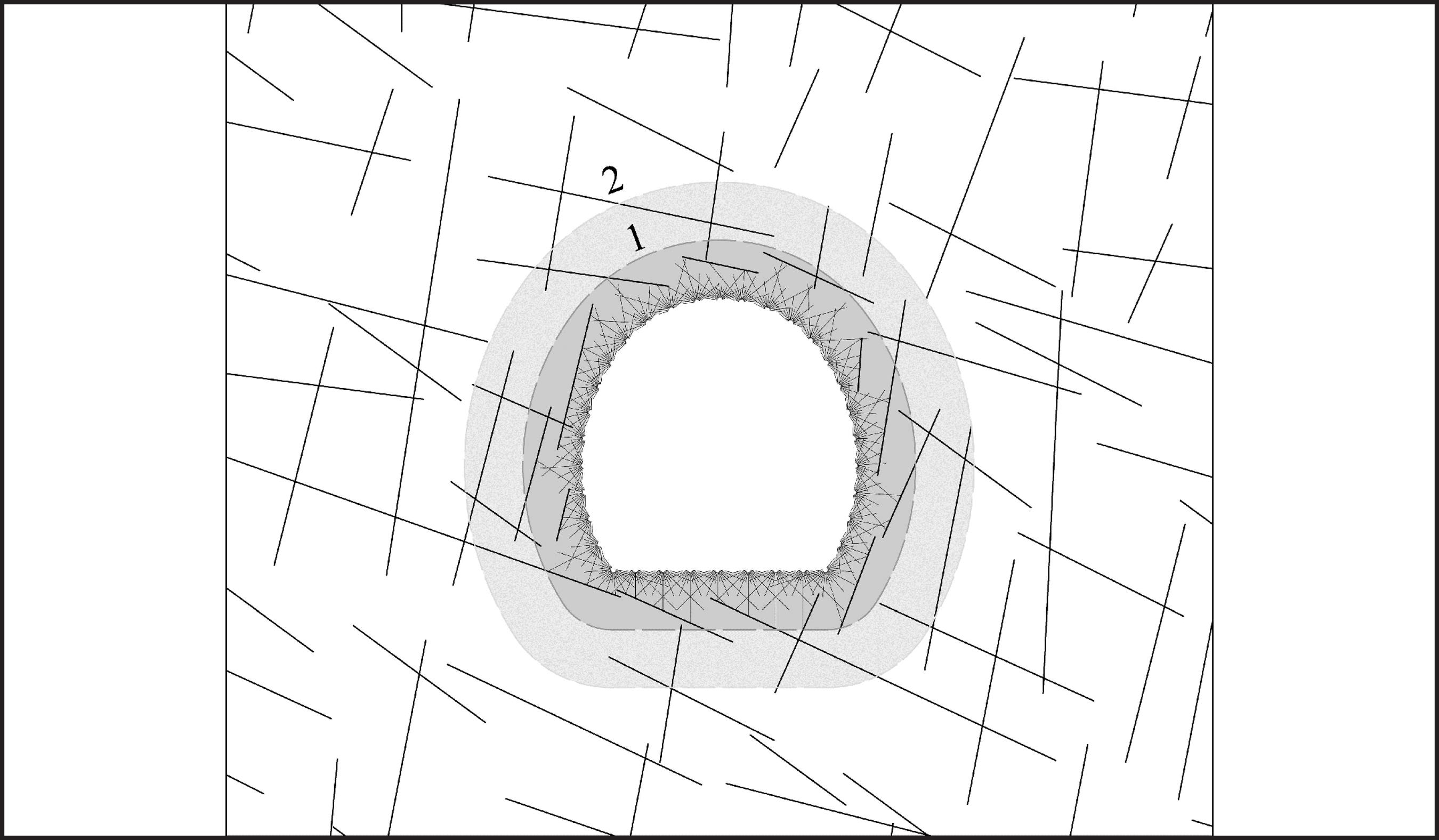
The second situation is when the primary block size is smaller than the maximum length of blast induced radial cracks. In this case, pressure wave propagation is being limited by preexisting joints in rock mass, and therefore blast-induced radial cracks are limited in their length by preexisting joints, Figure 5. It is obvious that more jointed rock masses are less subjected to blast induced damage and vice versa. The size of the blast damaged zone, in this case, depends primarily on maximum distance between preexisting joints in rock mass, or primary block size.
Blasting in rock mass where primary block sizes are smaller than the maximum length of the blast-induced radial cracks. Line 1 marks maximum length from contour blastholes to preexisting rock joints. Line 2 marks maximum length of blast induced radial cracks in monolith block. As can be seen, preexisting joints in rock mass are limiting radial crack propagation and therefore the blast damaged zone around the excavation has a smaller extent.
3.2 Quantification of the rock mass properties in the blast-damaged zones
Rock mass is presented as a set of monolith blocks intersected by joints and the first parameter that described the blocky structure of rock mass was the Geological Strength Index (GSI) (Hoek 1994HOEK, E. Strength of rock and rock masses, ISRM News Journal, v. 2, n.2, p. 4-16, 1994.). GSI describes rock mass based on the number of joint sets and the quality of the joint walls and is incorporated in the Hoek-Brown failure criterion (Hoek and Brown 1988HOEK, E., BROWN, E.T. The Hoek-Brown failure criterion - a 1988 update. In: CANADIAN ROCK MECH. SYMP., 15. Proc. In: Curran, J. H. (Ed.). Toronto: Civil Engineering Dept., University of Toronto, 1988. p. 31-38.; Hoek et al. 2002HOEK, E., CARRANZA-TORRES, C. Corkum, B., Hoek-Brown criterion - 2002 edition. Proc. NARMS-TAC CONFERENCE. Toronto: 2002, v. 1, p. 267-273.). Explosive detonation creates tension cracks in monolith blocks in the rock mass. The rock breakage by explosives theory (Torbica and Lapcevic 2014TORBICA, S., LAPCEVIC, V. Rock breakage by explosives. European International Journal of Science and Technology, p. 96-104, 2014.) made it possible to predict blast-induced radial crack length and density around the blasthole. Explosive detonation in contour blastholes creates the shape of excavation, but inevitably creates radial tension cracks in surrounding rock mass and damages it. Therefore, it is clear that rock mass around the excavation becomes more jointed. Said in other words, the zone around the excavation has a decreased GSI value when compared to the undisturbed rock mass. Using this principle, it is possible to determine strength parameters of rock mass in the blast damaged zone by choosing the proper GSI value for its quantification. Since rock mass in a blast damaged zone becomes more jointed, the GSI value for this part of rock mass should be chosen from the adjacent row below the GSI value for undisturbed rock mass. This corresponds to the fact that rock mass in the blast damaged zone has one joint set more (blast-induced cracks) than that of the undisturbed rock mass. In this manner, the GSI value of undisturbed rock mass is being decreased for 10 points. Quality of surface walls for blast-induced radial cracks will not be decreased in comparison with preexisting joints and therefore the GSI value should not be decreased regarding this criterion. Figure 6 illustrates the selection of the GSI value for blast damaged zone and equation (16) shows how this value can be calculated.
where: GSIbdz - GSI value in blast damaged zone
GSIurm - GSI value of undisturbed rock mass
4. Comparison between the modeled rock mass, with and without the damaged zones
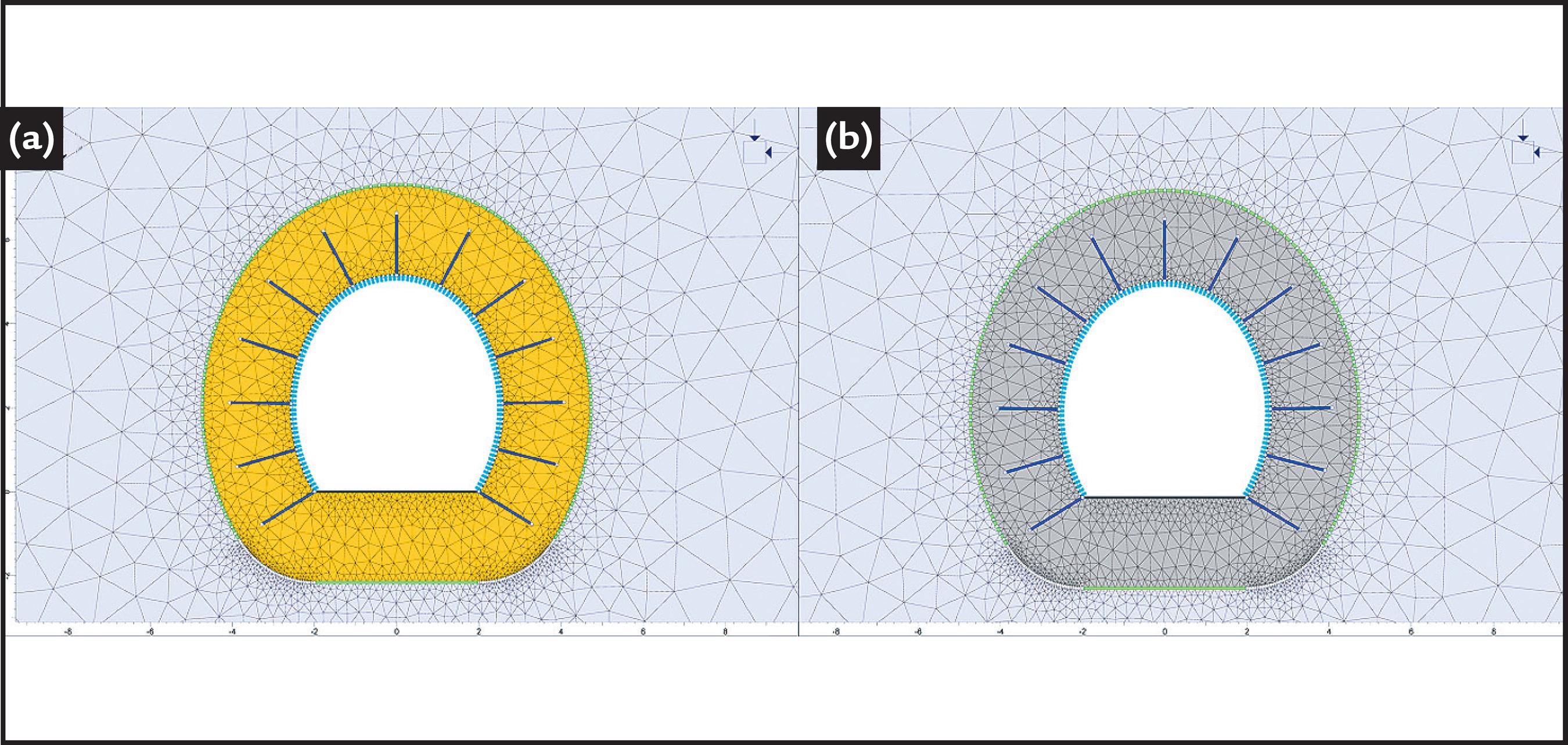
To describe and show the practical usage of the proposed method of blast-induced damage quantification, a typical tunneling situation was modeled using FEM and Phase2 software (Rocscience Inc.) for modeling. Table 2 presents the monolith and rock mass parameters (Hoek-Brown failure criterion) of the undisturbed rock mass and blast-damaged zones. The field stress components used in these examples are equal to 10 MPa (σ1 = σ3 = σz). Figure 7 shows two models, one that is used for analysis of the tunnel excavation without the blast-damaged zone and another for analysis with the blast-damaged zone (r4 = 2.16m = radius of damaged zone). Each model has the same support system installed and analyzed. This system consisted of 5 cm thick concrete (σc = 40MPa, σt = 3MPa E = 30GPa, Poisson ratio ν = 0.15) and fully bonded bolts with 1.6 m length (D = 19mm, E = 200GPa, and Tensile capacity of 0.072 MN).
Figure 8 presents the support capacity plots for the two models. Figure 9 presents a comparison between the maximum axial forces in the bolts with the marked tensile capacity for the two models. From these, it is obvious that in the case where blast-damaged zones are included in the analysis, the support system is subjected to higher loading which leads to safety factor decrease. Table 3 presents the maximum support loads.
Support capacity plots – a) model without blast-damaged zones b) model with blast-damaged zone
Maximum axial forces induced along bolts a) model without blast-damaged zone b) model with blast-damaged zone
5. Comparison between the proposed method for blast-damaged zone quantification and quantification using the blast damage factor D
As mentioned by Hoek (2012)HOEK E. Blast damage factor D. Technical note for RocNews, 2012., in the case of poor blasting, it can be expected that the blast-induced damage in the surrounding rock mass extends 2-3m. Kwon et al. (2009)KWON, S., LEE, C.S., CHO, S.J., JEON, S.W., CHO, W.J. An investigation of the excavation damaged zone at the KAERI underground research tunnel. Tunnelling and underground space technology, n. 24, p. 1-13, 2009. reports values in the same range. To quantify damage in the excavation walls, Hoek introduced the blast damage factor D and incorporated it into Hoek-Brown's failure criterion. If blasting is poorly done, it is suggested that D = 0.8. It has to be mentioned that this suggestion does not explain what is poor blasting and how to determine whether the used blasting pattern will give poor or good results. So, it is possible to describe the blasting process as poor only if it is already done. But, how to quantify and describe blasting quality before it is done?
We define poor blasting as blasting where contour blastholes are drilled with a smaller span between them and charged with the same amount of explosive as all other blastholes. If the contour blastholes, in the blasting pattern used to create tunnel shape shown in Figure 10, are charged the same as all other blastholes, we have a typical example of poor blasting. To compare these two methods for quantification of blast-induced damage in the rock mass, two FEM models were set up under the same loading and geometry conditions. The first model describes quantification using the blast damage factor D (D = 0.8). The damage zone extent is considered to be equal to the extent of zone r4 (2.16 m). This makes it possible to compare the two models. The second model's analyzed damaged zone was as described in section 4. In Table 4, the rock mass parameters used in these models are shown. In Figure 10, the FEM models used for analyses are shown. The support system is the same as used in the examples of section 4.
FEM models used for analysis a) damaged zone quantified using D=0.8 b) damaged zone quantified as proposed in this paper
Figure 11 presents the support capacity plots for concrete. Figure 12 presents the maximum axial forces along the bolts for the two models. From these plots, it can be seen that the support loading intensity is similar in both cases. Table 5 presents the maximum loading of the support systems in these cases.
Support capacity plots – a) model where blast-damaged zone is quantified using D=0.8 b) where blast-damaged zone is quantified using method proposed in this paper
Maximum axial forces induced along bolts a) model where blast-damaged zone is quantified using D=0.8 b) where blast-damaged zone is quantified using method proposed in this paper
6. Controlling blast-induced damage
It has been shown that the extent of blast damaged zone (BDZ) depends on several factors, such as pressure on blasthole walls, size of primary blocks in rock mass and strength of monolith rock. One of these factors that can be controlled is blasthole pressure. Pressure on the blasthole walls can be controlled by changing amount of explosive charge inside the blastholes or changing radii of explosive charge and blastholes.
According to Torbica and Lapcevic (2014)TORBICA, S., LAPCEVIC, V. Rock breakage by explosives. European International Journal of Science and Technology, p. 96-104, 2014. burden for a blasthole can be calculated by the equation:
Where: B - burden; r4 – radius of cracking zone according to eqn. (15)
After insertion of equation (15) into (17) for n=4:
Form equation (18) pressure on the blasthole walls, which is the only controllable factor, can be expressed as:
Using equation (19), it is possible to calculate required pressure in order to break burden B that is left for contour blastholes. Therefore, for the borehole radius rh =0.051m in limestone with tensile strength σt=7MPa, Poisson's ratio ν=0.3, the required pressure to break 0.5 m thick burden equals to 543 MPa (~0.5 GPa). At this point it is possible to determine the maximum extent of blast damaged zone created by contour blastholes by calculating radius of cracking zone r4 for pressure of 0.5 GPa. For pressure 0.5 GPa using equation (15) radius of cracking zone r4 equals 0.68 m (~0.7 m) instead of 2.16 m (Ph=1.6 GPa) as shown in Table 1. Figure 13 illustrates how thickness of blastholes burden impacts damaged zone extent. It has to be mentioned that one should take care about the explosive charge in blastholes that are initiated before the contour blastholes. In fact, the explosive charge in these blastholes may produce much longer radial cracks than those from contour blastholes, if pressure is unreasonably high. Therefore, care should be taken when choosing explosive amount for each blasthole the in blasting pattern.
Illustration on how blast damaged zone extent can be controlled. Situation before contour blastholes initiation is shown. B1 and B2 are burdens for contour blastholes in two different situations. B2 is larger than B1 and therefore higher pressure in contour blastholes is required in order to break thicker burden B2. By careful design of blasting pattern, the burden of contour blastholes can be optimized in such manner that pressure in these blastholes is minimized.
According Chapman-Jouguet detonation theory, Chapman (1899)CHAPMAN, D. L. On the rate of explosion in gases. Philosophical Magazine. v. 47, n. 284, p. 90-104, 1899. (Series 5). DOI:10.1080/14786449908621243
https://doi.org/10.1080/1478644990862124...
and Jouguet (1905)JOUGUET, EMILE. Sur la propagation des réactions chimiques dans les gaz. [On the propagation of chemical reactions in gases]. Journal de Mathématiques Pures et Appliquées, series 6 (in French) p.347-425, 1905., pressure on the blasthole walls for explosives with density above 1 g/cm3 can be calculated as:
Where: ρe – density of explosive (g/cm3); D – detonation velocity of explosive (km/s).
For explosive with density below 1 g/cm3 pressure on the blasthole walls is calculated by:
Equations (20) and (21) assume that blasthole if fully filled with explosive, if blasthole radius and radius of explosive charge differ or blasthole is not fully filled with explosive, pressure on the blasthole walls is calculated by:
Where: Ph – Pressure on the blasthole walls (GPa), Pd – Detonation pressure (GPa), de – Diameter of explosive charge, dh – Blasthole diameter
Equation (22) provides a very useful tool for estimating the amount of explosive needed to acquire specific pressure value. From equation (22) we are able to express diameter of explosive charge as follows:
To achieve pressure of 0.5 GPa on blasthole walls using boreholes with 0.102 m in diameter and explosive with detonation pressure of 1.6 GPa, diameter of explosive charge should be ~0.069 m which corresponds to a standardized diameter of 70 mm explosive patrone.
7. Discussion
It has to be stated that there is no model for the exact assessment of the extent and quantification of blast-damaged zones. Hoek-Brown's failure criterion has incorporated the blast damage factor D as a parameter that describes the blasting damage in the rock mass. This parameter only describes the blasting process that has been done, but one cannot describe the blasting process beforehand, in the project phase. On the other hand, there is a common misuse of blast damage factor in the way it is applied to the whole rock mass. In this way, one underestimates the whole rock mass properties instead of the limited zone around the excavation. Herein, a method for the precise assessment of blast-damaged zone's shape and extent is proposed, and also a method for the quantification of the rock mass parameters in these zones. With this suggestion, it is possible to define the blasting process as “good” or “bad” before it is done. One can easily assess the damaged zone extent based on the rock and explosive properties and quantify it using the Hoek-Brown's failure criterion.
Results presented in this paper show that there is an obvious need to differentiate between the undisturbed rock mass and the blast-damaged zones. It has been shown that in the case of modeling the blast-damaged zones, higher support loading occurred as was expected. When comparing the proposed method and quantification using the blast damaged factor D, results showed that in both cases similar support loads occurred. The main difference between these methods is in fact that when using the blast damage factor, one has to rely on the supposed extent of the blast-damaged zone being assessed, while the proposed method herein is able to offer a precise assessment of the blast-damaged zone extent. On the other hand, quantification using the blast damage factor is highly subjective, since it is not possible to say whether the blasting pattern that will be used for excavation will provide severe rock mass damage or not. In contrast, the proposed method offers an objective quantification of the damaged zone in the surrounding rock mass. In addition, the nature of the blast damage factor is empirical and its values are estimated based on reverse analysis. This makes it highly case dependent. The method that is proposed here is based on constitutive relationships that describe rock breakage by explosives.
At the end of this paper, it is explained how blast-induced damage around excavations can be controlled. Using principles described here and relationships that are used to calculate pressure on the blasthole walls, it is possible to determine exact amounts of explosive inside contour blastholes that are necessary to break their burden. It has to be emphasized that it is not the size of the blast damage zone that is crucial for analysis, but the relative size of the blast damage zone size and the size of primary rock blocks. In fact, small primary blocks may even be crushed by small amounts of explosive. Said in other words, with decreasing primary block size impact of blast-induced damage increases.
8. Conclusion
As it is already known, there are plenty of methods for assessment of blast-damaged zones. Also, there is a lack of precise methods for assessing the extent and quantification of these zones. Many of the existing methods are empirical and highly case dependent, while on the other hand, theoretical methods have limited applicability. An important part of the new rock breakage theory is presented, making it possible to estimate the length and density of the tension (radial) cracks caused by explosive charge initiation. Based on this theory, the method for the blast-damaged zone extent and quantification of its rock mass properties has been proposed. It explains how to assess the zone's shape and extent based on the blasting pattern that is used, the main properties of rock mass, and the explosive used. To show the importance for analysis of blast-damaged zones, a typical tunneling situation was modeled using FEM. Analysis showed that in case when blast-damaged zones were included in the model, much higher support loads occurred, as was expected. Furthermore, a comparison between the quantification of the blast-damaged zones using blast damage factor D and the herein proposed method was done. Results showed that in both cases, the support loads are in the same magnitude order, which also confirms that the proposed blast-damaged zone quantification method is correct. Finally, a discussion between these two methods for blast-damaged zone quantification has been presented, whereupon it can be concluded that the proposed method is more objective than quantification using the blast damage factor D. Controlling the blast-induced damage around underground excavations is of great importance and here it is explained how pressure on the blasthole walls can be controlled in order to reduce the extent of blast-damaged zone.
References
- ALIABADIAN, Z., SHARAFISAFA, M., MORTAZAVI, A., MAAREFVAND, P. Wave and fracture propagation in continuum and faulted rock masses: distinct element modeling. Arabian Journal of Geosciences p. 5021-5035, 2014. DOI 10.1007/s12517-013-1155-3.
» https://doi.org/10.1007/s12517-013-1155-3 - ASH, R. L. The mechanics of rock breakage. Pit and Quarry I, (Aug) p. 98-112. Part , II (Sept) p. 118-123. Part III, (Oct), p. 126-131. Part IV (Nov), p. 109-118, 1963.
- BRINKMANN, J. R. Separating shock wave and gas expansion breakage mechanisms. PROC.2ND INT. SYMP. ON FRAGMENTATION BY BLASTING. Keytone, Colorado USA: 1987. p. 6-15.
- BRINKMANN, J. R. An experimental study of the effects of shock and gas penetration in blasting. PROC. 3RD INT. SYMP.ON FRAGMENTATION BY BLASTING, Brisbane, Australia: 1990. p. 55-66.
- CHAPMAN, D. L. On the rate of explosion in gases. Philosophical Magazine v. 47, n. 284, p. 90-104, 1899. (Series 5). DOI:10.1080/14786449908621243
» https://doi.org/10.1080/14786449908621243 - DRUKOVANYI, M. F., KRAVTSOV, V. S., CHERNYAVSKII, Y. E., REVA, V. V., ZERKOV, S. N. Calculation of fracture zones created by exploding cylindrical charges in ledge rocks. Soviet Mining Science, v. 12, n. 3, p. 292-295, 1976.
- HOEK, E., BROWN, E.T. The Hoek-Brown failure criterion - a 1988 update. In: CANADIAN ROCK MECH. SYMP., 15. Proc. In: Curran, J. H. (Ed.). Toronto: Civil Engineering Dept., University of Toronto, 1988. p. 31-38.
- HOEK, E. Strength of rock and rock masses, ISRM News Journal, v. 2, n.2, p. 4-16, 1994.
- HOEK, E., CARRANZA-TORRES, C. Corkum, B., Hoek-Brown criterion - 2002 edition Proc. NARMS-TAC CONFERENCE. Toronto: 2002, v. 1, p. 267-273.
- HOEK, E, DIEDERICHS, M.S. Empirical estimation of rock mass modulus. International Journal of Rock Mechanics and Mining Sciences, n. 43, p. 203-215, 2006.
- HOEK E. Blast damage factor D. Technical note for RocNews, 2012.
- HOLMBERG, R. Charge calculation for tunnelling. In: HUSTRULID W.A. (Ed.), Underground Mining Methods Handbook, Soc. Min. Metall. Explosives, p.1580-1589, 1982.
- HUSTRULID, W., LU, W. Some general concepts regarding the control of blast-induced damage during rock slope excavation. Fragblast-7, p. 595-604, 2002.
- HUSTRULID, W., JOHNSON, J. A gas pressure-based drift round blast design methodology. In: SCHUNNESSON, H. NORRDLUND, E. Proceedings, MassMin 2008. Lulea, p. 567-669, June 9-11, 2008.
- HUSTRULID, W. Some comments regarding development drifting practices with special emphasis on caving applications. PROC. CAVING 2010 SYMP. In: POTVIN, AGG. On Block and Sublevel Caving. Perth Australia. p. 3-44, 2010.
- JÄRNVÄGS, A. M. A. Swedish National Railway Authorities Complement to AMA 83. Rock Technique Rpt. TM-95-060 1996-09-01. Banverket, Borlänge, 1996.
- JOUGUET, EMILE. Sur la propagation des réactions chimiques dans les gaz. [On the propagation of chemical reactions in gases]. Journal de Mathématiques Pures et Appliquées, series 6 (in French) p.347-425, 1905.
- KANCHIBOLTA S. S., VALERY, W., Morrell, S. Modeling fines in blast fragmentation and its impact on crushing and grinding. Proc. of Explo. '99-A CONFERENCE ON ROCK BREAKING. Brisbane, Australia: The Australasian Institute of Mining and Metallurgy, p. 137-144, 1999.
- KWON, S., LEE, C.S., CHO, S.J., JEON, S.W., CHO, W.J. An investigation of the excavation damaged zone at the KAERI underground research tunnel. Tunnelling and underground space technology, n. 24, p. 1-13, 2009.
- LANGEFORS, U., KIHLSTROM, B. The modern techniques of rock blasting. New York: John Wiley and Sons, 1973.
- OUCHTERLONY, F. Prediction of crack lengths in rock after cautious blasting with zero inter-hole delay. Int. J. for Blasting and Fragmentation, n. 1, p. 417-444, 1997.
- OUCHTERLONY, F., OLSSON, M., BERGQVIST, I. Towards new Swedish recommendations for cautious perimeter blasting. Fragblast, v. 6, n. 2, p. 235-261, 2002.
- Rocscience Inc., Phase2 Version 7.0 - Finite Element Analysis for Excavations and Slopes. www.rocscience.com, Toronto, Ontario, Canada, 2008.
» www.rocscience.com - SAIANG, DAVID. Blast-induced damage: a summary of SveBeFo investigations. Luleå: Luleå tekniska universitet, (Technical report / Luleå University of Technology, n. 21, 2008). 42 p.
- SENUK, V. M. The impulse from an explosion and conditions for its greater utilization in crushing hard rock masses in blasting.: Soviet Mining Science p. 22-27, 1979.
- TORBICA, S., LAPCEVIC, V. Rock breakage by explosives. European International Journal of Science and Technology, p. 96-104, 2014.
- TORBICA, S., LAPCEVIC, V. Model for estimating blasted rock fragmentation. In: SGEM GEOCONFERENCE ON SCIENCE AND TECHNOLOGIES. In: Geology, Exploration and Mining. www.sgem.org, SGEM2014 GeoConference Proceedings, ISBN 978-619-7105-09-4 / ISSN 1314-2704, June 19-25, 2014, v. 3, p. 379-386, 2014.
» www.sgem.org
Publication Dates
-
Publication in this collection
Oct-Dec 2015
History
-
Received
16 Apr 2015 -
Accepted
11 Aug 2015