Abstract
This article presents a numerical model based on the finite difference method for the physical and geometric non-linear analysis of a one-dimensional consolidation problem regarding a saturated, homogeneous and isotropic soil layer with low permeability and high compressibility. The problem is formulated by adopting the void ratio as the primary variable, considering a Lagrangian movement description. The physical non linearity is introduced on the formulation by the constitutive law defined as effective stress and permeability void ratio functions. Based on this numerical model, a computational system named AC-3.0 was developed, which has been verified and validated in terms of the temporal variation of the void ratio distribution throughout the soil layer, by comparing the numerical results with analytical and numerical solutions found in literature for some specific scenarios. Knowing the void ration distribution,it is possible to obtain secondary variables such as: superficial settlement, effective stress and excess of pore water pressure.The importance of the non-linear formulation is highlighted for the analysis of problems related to material presenting high compression and a very high initial void ratio.
keywords:
non-linear geometric analysis; finite difference method; Lagrangian formulation; physical non-linearity; self-weight consolidation problem
1. Introduction
Consolidation is a physical phenomenon that can occur in porous media and is related to the temporal dissipation of the excess of pore water pressure generated by anexternal force (body and/or surface loads), causing displacement, strain, and stress field variations throughout the soil layer. This problem was initially studied by Terzaghi, in 1923,who formulated the classical consolidation theory (Schiffman, 2001). Terzaghi adopted some simplified hypotheses, such as: the soil layer's material is homogeneous and saturated; the solid particles and the water are incompressible; the water flow and the deformation occur only in a vertical direction; the strains are small and time-independent; the Darcy Law is valid; and, the permeability coefficient and the volumetric compressibility modulus does not vary during the process.
Although these simplified hypotheses are unreal for some scenarios, the Terzaghi's theory, by its mathematical relative simplicity, provides very good results for some practical engineering problems. Nevertheless, in some engineering practical situations, such as mining tailings deposits/dams and the dredging process, it is necessary toadopt a more precise theory involving physical and geometric non-linearity,since the tailings(ormud) generated by the mining plant and dredging activities are very soft and present a high initial void ratio distribution when placed in the field.
Bartholomeeusen et al. (2002) highlight the importance of using a non-linear constitutive law in order to analyze the consolidation problem related to the dredging and embankment of soft soil. Yao et al. (2002) highlight the importance of studying this phenomenon in the sense of optimizing the storage capacity and the consolidation time reduction of the high amount of tailings generated by the mining and civil construction industries. In this context, as well highlighted by Abu-Hejleh et al. (1996), the computational models are valuable tools for the mining reclamation process, since they provide the storage capacity of the tailings disposal along with the estimated duration of the consolidation process (Almeida et al. 2005). Penna and Oliveira Filho (2012) highlight the importance of the slope stability of the tailings retaining structures during their constructive phase.
Herein, the governing differential equation and the finite difference equations of the non-linear, physical and geometric, one dimensional consolidation problem taking into account body force effects are presented. The numerical model generated was implemented into a computational system named AC (Analysis of Consolidation) in its third version. The previous version was developed by Nogueira (2002) and Ferreira and Nogueira (2004). This computational system is verified with the analytical solution provided by Gibson et al. (1967) and Xie and Leo (2004); and, with other numerical solutions presented by Yao and Znidarcic (1997) and Batholomeeusen et al. (2002).
2. Non-linear consolidation problem's governing equation
The theory of the non-linear one dimensional consolidation problem presented by Gibson et al. (1967) considers the following hypotheses: the porous media is considered as homogeneous, saturated and normally consolidated; solid particles and water are incompressible; the deformation of the media is due to solid particle rearrangement followed by the flow of the water into pores;the volume of the solid remains constant during the process; there is no restriction related to the magnitude of the deformation; the strain and the water flow occur in a vertical direction; the process is induced by the body and/or surface monotonic loads; the strain is time-independent; the permeability coefficient and the volumetric compressibility vary during the process with the void ratio variation.
By considering the above hypotheses and adopting a Lagrangian movement description, one can obtain the following non-linear differential partial equation, which represents the conservation and balance of the porous media mass (Gibson et al., 1967), in terms of the reduced coordinate (z) and the time (t):
where e is the void ratio; γs is the self-weight of solid particles; γw is the self-weight of water; k and are, respectively, the permeability coefficient and the effective stress which is defined as a void ratio function named of constitutive laws. The reduced coordinate (z) is defined in terms of the Lagrangian coordinate (a) as:
where (a,0) represents the initial void ratio distribution, which inrelation to the solid particle volume isbetween the fixed referential and a generic point. Thus, Equation (1) can be rewritten in a compact form as follows:
in which:
are functions which depend on the constitutive laws and theirderivatives related to the void ratio. The constitutive laws are defined by field and laboratory observation (Silva and Azevedo, 1999). Many constitutive laws can be found in literature. Based on the Hydraulic Consolidation Test (HCT), Liu and Znidarcic (1991) suggested the following constitutive laws:
or
for which A, B, C, D, and ZL are constitutive parameters determined by curves adjusted for the procedure. From Equation (7b) it is possible to obtain:
Xie and Leo (2004), on the other hand, suggested the following ones:
or
where 0 is the previous effective stress on the soil layer; mv is the volumetric deformability modulus on confined compression (made constant during the process); e00 is the initial void ration on the soil layer's surface; and, k00 is the permeability coefficient related to the initial void ratio for the soil layer's surface. From Equation (8b), it is possible to obtain:
where av is the compressibility coefficient (made constant during the process).
Equation (3) can be written in a normalized form as suggested by Gibson et al. (1981) by doing:
where Z and T are, respectively, the normalized height and time; z is the height of a generic point on the soil layer defined in terms of reduced coordinated according to the Equation (2); Hr is the initial thickness of the soil layer in the reduced coordinate system; H0 is the initial thickness of the soil layer; is the function defined in Equation (6) corresponding to the initial void ration on the soil layer's surface (e00). Using the definition on Equations (9) to (11), one can obtain the following normalized governing equation:
where
Equation (12) must obey the initial condition, e (Z,0) = e (σ' (Z,0) ), where:
The second term of Equation (15) represents the effective surcharge of the soil layer weight on the Z point. In addition, Equation (12) must obey the following boundary conditionon the surface or top of the soil layer (Z=1), considered as a drained boundary:
in which Δq is the incremental load applied instantaneously on the surface and kept constant during the process. For the base of the soil layer (Z=0), the condition depends on the drainage. If the base is considered as a drained boundary, the problem is identified as double drained where:
For a single drained condition, when the base is considered as an impermeable boundary, one can have
Once the void ratio distribution (primary variable)is obtained by solving Equation (12), one can obtain the secondary variables such as: settlement, total and effective stress, and pore water pressure (total, initial and excess). The settlement S(T) can be obtained by executing:
The total stress distribution σ(Z,T) can be obtained with:
where Hw is the water thickness above the soil layer surface. The effective stress can be obtained by adopting one of the constitutive laws presented Equation (7a) or (8a).Once the total and effective stressesare known, the pore water pressure (p) can be obtained according to the Terzaghi's principle, by using:
The hydrostatic pore water pressure pss (Z,T) is given by:
where
is the soil layer's height at the reduced coordinate. Finally, the excess of pore water pressures is obtained by doing:
3. Finite difference equations of the non-linear consolidation problem
The non-linear second order differential partial equation which represents the non-linear consolidation problem (Equations 1, 3 and 12), is considered as a high complexity resolution differential partial equation. For some simplified situations, it is possible to obtain an analytical solution such as the solution presented by Xie and Leo (2004). However, some situations having complex geometry, loading and boundary conditions indicate the use of some approximation technique which transforms the differential equation into an algebraic equation system. By doing this, it is possible to obtain at least an approximated solution for the complex problem. Many different methods can be defined depending on the adopted discretization technique.
The finite difference method (FDM), adopted herein, divides the domain problem into a finite number (npoin) of discreet points named nodal points (k point). The set of nodal points is the nodal point mesh. For each nodal point, the derivative parcels of the differential partial equation are changed by the variation rate of the primary variable.
As Equation (12) involves a time derivative, the normalized time (T) is divided into finite increments (ΔT) and a time march is defined by the θ constant, which localizes the time function into the time interval from T to T+ΔT and defines the kind of algorithm: θ=0.0 for the explicit algorithm, θ=0.5 for the implicit algorithm (Cranck-Nicholson), and θ=1.0 for the purely implicit algorithm. Using a central difference approximation, it is possible to obtain the following approximation for the first and second order of the space derivative which appears in the governing equation:
Applying the approximation described by Equations (24) into Equation (12), one can obtain the following algebraic equation system on a generic k nodal point within the problem domain:
where:
and:
For the point on the top of soil layer (k=npoin; Z=1), considered as a drained contour, the boundary condition equation (Equation 16) is given by:
where:
For the point on the base of soil layer (k=1; Z=0) the boundary condition equation is given by:
For the drained contour (Equation 17a):
For the impermeable contour (Equation 18):
Equations (25), (28) and (30) can be arranged into a compact form by making:
where:
Due to the non-linear nature of the constitutive laws, Equation (33) is also non-linear. Then, an iterative process is necessary in order to obtain the equation solution.This study adopts the Picard Method (Pereira, 2017) as the solution strategy.
4. Verification examples
Three examples are now presented.The first example refers to the non-linear analyses of the consolidation problem due to the body and surface load as suggested by Xie and Leo (2004). The second example considers a specific scenario of a mining industry related to a material with initial void ratio distribution (Yao and Znidarcic, 1997). The last one was proposed by Bartholomeeusen et al. (2002) and is related to a consolidation problem due to the self-weight force of a sedimentproduced by a dredgingprocess. The results presented by Xie and Leo (2004) are analytical, while the results presented by Yao and Znidarcic (1997) and Bartholomeeusen et al. (2002) are numerically obtained by different computational systems.
4.1 Example 1
This first example deals with the consolidation problem in the context of the physical and geometric non-linearity of a saturated, homogeneous, isotropic and soft soil layer. The initial thickness of the soil layer is 10m. The soil layer presents an initially uniform distribution of effective stress (q'0) of 10kPa and is subject to a uniform surface load of 100kPa instantaneously applied and kept constant throughout the time limit.This soil layer is subject to a doubled drainage boundary condition. The following material parameters were considered: mv of 0.004kPa-1; e00 of 3.0; k00 of 10-9m/s; γs of 27.5 kN/m3 and γw of 10kN/m3. The initial thickness in the reduced coordinate is equal to 2.5m according to Equation (11), while Equations (6), (9) and (10) respectively provide: g2(e00)=1.5625x10-9m2/s, Z=0.4z and T=2.5x10-10t. According to the constitutive law indicated by Equations (8c), one can obtain:
The initial condition in terms of the void ratio is obtained by Equation (39) according to the following distribution of the effective stress along the soil layer:
According to this equation, the initial void ratio on the base and top of the soil layer is respectively given by 2.36 and 3.0. According to the Equations (16) and (17) the effective stress at the top (Z=1) and base (Z=0) of soil layer is, respectively, 110kPa and 153kPa, leading to a boundary condition in terms of the void ratio of 1.68 and 1.25, respectively.
Figure 1 presents the numerical results obtained with theAC-3.0 system by adopting a finite difference mesh with 21 nodal points and the implicit algorithm (q=1.0) with the real time increment (Δt) of 9.855x106s. The tolerance for Picard's algorithm was 10-5. Figure 1 apresents the time variation of the void ratio distribution, while Figures 1b presents the time variation of the average degree of consolidation defined as:
where:
for which, Δp is the excess of pore water pressure given by Equation (23); and T=0+ represents the time instant immediately after the instantaneous surface load application.
The numerical results are in a good agreement with the analytical solution presented by Xie and Leo (2004). This verifies the implementation of the AC-3.0 computational program. At the end of the process, the void ratio distribution tends to a linear variation, such as the initial distribution. As can be seen in Figure 1b, more than 70% of consolidation occurs in a normalized time around 0.1, while according to the linear theory (Schiffman, 2001), this same average degree of consolidation is observed at a normalized time of 0.4. The velocity of the consolidation process is higher when analyzed in the context of the non-linear theory than when analyzed in the context of the linear theory.
4.2 Example 2
The second example presents the consolidation analysis of a saturated, homogeneous, isotropic and soft soil layer withhigh initial void ratio uniform distribution subject to a self-weightload. The initial thickness of the soil layer is 17.85m. The uniform distribution of the initial void ratio of 32.42 is considered as the initial condition. The base of the soil layer is considered impermeable, so the problem is analyzed adopting asingle drainage boundary condition. The constitutive law (Equation 7) proposed by Liu and Znidarcic (1991) is adopted and the following material parameters were considered:A=13.49; B=−0.319; ZL=0.064kPa; C=3.84x10-12m/s; and, D=3.5. Also, considered were: gs is equal to 26.58kN/m3; and γw is equal to 9.81kN/m3. This scenario was analyzed numerically by the software Condes0 (Yao and Znidarcic, 1997).
The initial thickness for thereduced coordinate is equal to 0.534m according to Equation (11), while Equations (6), (9) and (10) respectively provide:g2(e00)=1.41x10-11 m2/s, Z=1.87z and T=4.94x10-11t. The boundary condition on top of the soil layer is 32.42 as the soil layer is only subject to a self-weight load. However, the boundary condition on the base of the soil layer is given, adopting Equations (7d), by:
Figure 2 presents the numerical results obtained in theAC-3.0 system by adopting a finite difference mesh with 61 nodal points and the implicit algorithm (θ=1.0) with the real time increment (Δt) of 3.15x106s. The tolerance of Picard's algorithm was 10-5. Figure 2a presents the time variation of the void ratio distribution, while Figure 2b presents the variation in time of the soil layer thickness. The numerical results obtained by the AC-3.0 software are in good agreement with those of software Condes0. The final void ratio distribution is non-linear with the minimal value located at the base of the soil layer. No significant variation of the soil layer thickness is observed after 20 years. This information is very important in the field of tailings disposal in the mining process.
4.3 Example 3
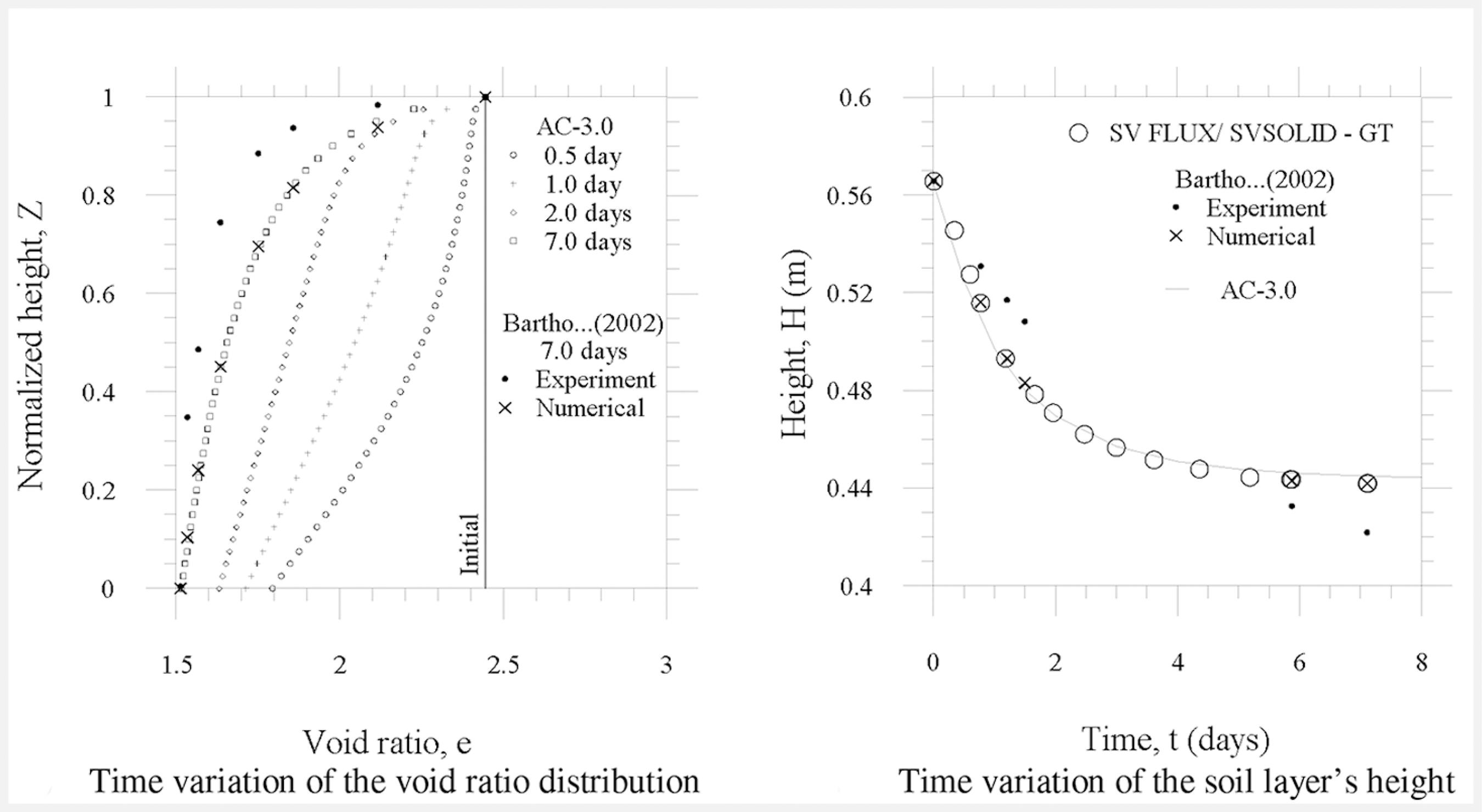
Bartholomeeusen et al. (2002) studied the consolidation problemfora sediment of the Schelde River (Antwerp, Belgium) provided by a dredging process. The consolidation problem was considered for only the self-weight load. Bartholomeeusen et al. (2002) adopted a different constitutive law in order to analyze its influence on the process. According to these authors, when compared to the large scale experimental data,the best numerical results were obtained by adopting the constitutive law (Equation 7) presented by Liu and Znidarcic (1991).
The homogeneous, isotropic and saturated sediment was placed into a consolidation column withan initial thickness of 0.565m. The sediment layer is submitted to a single drainage from its top. The following material parameters were adopted: γs=27.2kN/m3; γw=10kN/m3; A=1.69, B=−0.12, ZL=0.046kPa; C=4.14x10-9m/s; and, D=6.59. The initial thickness of thereduced coordinate is equal to 0.16m according to Equation (11) by considering a uniform initial void ratio distribution of 2.45. Equations (6), (9) and (10) respectively provide: g2(e00)= 6.15x10-9 m2/s, Z=6.25z and T=2.40x10-7t. The boundary condition on top of the soil layer is 2.45, as the soil layer is subject only to a self-weight load. However, the boundary condition on the base of the soil layer is given when adopting the Equations (7d), by:
Figure 3 presents the numerical results obtained by AC-3.0 system by adopting a finite difference mesh with 41 nodal points and the implicit algorithm (θ=1.0) with the real time increment (Δt) of 8.6x103s. The tolerance of Picard's algorithm was 10-5. Figure 3a presents the time variation of the void ratio distribution, while Figure 3b presents the variation in time of the soil layer thickness. The numerical results obtained by the AC-3.0 software are in a good agreement with the numerical results presented by Bartholomeeusen et al. (2002) at the end of the consolidation process. No significant variation of the soil layer thickness is observed after 7 days. The final void ratio at the base of soil layer was found to be around 1.54, while on the top of this layer the void ratio was kept constant and equal to 2.45.
The time variation of the soil layer thickness obtained by AC-3.0 software (Figure 3b) agrees with the result presented by Bartholomeeusen et al. (2002) and the results provided by the software SVFLUX/SVSOLID GT (SoilVision Systems Ltda, 2017). In the context of a practical engineering problem, the numerical results are in a good agreement with the large scale experimental data.
5. Conclusions
A soft soil layer that is highly compressible and with a high initial distribution void ratio subject to a consolidation process due to self-weight and/or surface load must be analyzed in the context of the physical and geometric nonlinearities. The physical nonlinearity should take into account the constitutive law that plays a fundamental role in the numerical simulation.The numerical/computational model based on the FDM presented herein was verified by comparison with analytical and numerical solutions available in literature. Also, the model was validated by comparison with field data that is also available in literature. However, great effort must be made regarding constitutive law definition and field monitoring in order to improve the quality of the numerical simulation.
Acknowledgements
The authors are grateful for the financial support received from CAPES, CNPq, FAPEMIG, Fundação Gorceix, PPGEM/UFOP, PROPEC/UFOP, PROPP/UFOP. The first author is grateful for the grant received by CAPES. The second author is grateful for the grant received by FAPEMIG. They also acknowledge Harriet Konkel Reis for the editorial review of this text.
References
- ABU-HEJLEH, A. N., ZNIDARČIĆ, D., BARNES, B. L. Consolidation characteristics of phosphatic clays. Journal of Geothechnical Engineering, v. 122, n. 4, p. 295-301, 1996.
- ALMEIDA, F. E., OLIVEIRA FILHO, W. L., NOGUEIRA, C. L. Numerical analysis of the drying process of a fine tailings. REM: Revista Escola de Minas, v. 58, n. 4, p. 355-365, 2005. (in Portuguese).
- BARTHOLOMEEUSEN, G., SILLS, G. C., ZNIDARČIĆ, D., VAN KESTEREN, W., MERCKELBACH, L. M., PYKE, R., CARRIER III, W. D., LIN H., PNEUMADU, D., WINTERWERP, H., MASALA, S., CHAN, D. Sidere: numerical prediction of large-strain consolidation. Geotechnique, v. 52, n. 9, p. 639-648, 2002.
- FERREIRA, A. M., NOGUEIRA, C. L. Analysis of one-dimensional consolidation with large deformations using the finite difference method. Final Report of Beginners Research PIBIC 2003-2004 2004. 59 p. (in Portuguese).
- GIBSON, R. E., ENGLAND, G. L., HUSSEY, M. J. L. The theory of one-dimensional consolidation of saturated clays: 1. Finite non-linear consolidation of thin homogeneous layers. Geotechnique, v. 17, n. 3, p. 261-273, 1967.
- GIBSON, R. E., SCHIFFMAN, R. L., CARGILL, K. W. The theory of one-dimensional consolidation of saturated clays. II. Finite non-linear consolidation of thick homogeneous layers. Canadian Geotechnical Journal, v. 18, n. 2, p. 280-293, 1981.
- LIU, J., ZNIDARCIC, D. Modeling one-dimensional compression characteristics of soils. Journal of Geotechnical Engineering, v. 117, n. 1, p. 162-169, 1991.
- NOGUEIRA, C.L. Analysis of one-dimensional consolidation with large deformations using the finite difference method. Final Report of the Project TEC 1487/98 - FAPEMIG 69 p. 2002. (in Portuguese).
- PEREIRA, R. D. A non-linear analysis using the finite difference method for a one-dimensional consolidation problem Ouro Preto: Escola de Minas, Universidade Federal de Ouro Preto, 2017. 79 p. (Msc. Dissertation). (in Portuguese).
- PENNA, L. R., OLIVEIRA FILHO, W. L. Monitoring constructive pore water pressure. REM: Revista Escola de Minas, v. 65, n. 4, p. 443-448, 2012. (in Portuguese).
- SCHIFFMAN, R. L. Theories of consolidation University of Colorado at Boulder, 2001. 500 p.
- SILVA, W. S., AZEVEDO, R. F. Hydraulic Consolidation Test. In: CONGRESSO BRASILEIRO DE GEOTECNIA AMBIENTAL, 4, 1999. São José dos Campos. REGEO'99. São Paulo: ABMS, 1999. v. 1, p. 225-233. (in Portuguese).
- SOILVISION SYSTEMS LTDA. Verification Manual Saskatoon. Saskatchewan, Canada, 2017.
- XIE, K. H., LEO, C. J. Analytical solutions of one-dimensional large strain consolidation of saturated and homogeneous clays. Computers and Geotechnics, v. 31, n. 4, p. 301-314, 2004.
- YAO, D. T. C., OLIVEIRA-FILHO, W. L., CAI, X., ZINIDARCIC, D. Numerical solution for consolidation and desiccation of soft soils. International Journal for Numerical and Analytical Methods in Geomechanics, v. 26, n. 2, p. 139-161, 2002.
- YAO, D. T. C., ZNIDARCIC, D. Users Manual for Computer Program CONDES0 Boulder: FIPR, Department of Civil, Environmental and Architectural Engineering, University of Colorado, 1997. 98 p.
Publication Dates
-
Publication in this collection
Apr-Jun 2019
History
-
Received
18 Dec 2017 -
Accepted
26 Oct 2018

 Physical and geometric non-linear analysis using the finite difference method for one-dimensional consolidation problem
Physical and geometric non-linear analysis using the finite difference method for one-dimensional consolidation problem