Abstract
To optimize a mining project, it is necessary to deal with several technical aspects and constraints, such as orebody modelling, reserve estimation, blending strategy, optimal and operational pit designs, cost control, environmental issues, among others. In this sense, locating surface infrastructures is one of the most critical mine planning concerns, as approximating these facilities to the pit in order to reduce the operational costs, might interfere with future pit expansions in new favorable scenarios. In such cases, impacts on the project's net present value (NPV) are inevitable and must be technically dealt with, evaluating alternative scenarios to propose a strategy that increases profitability. The aim of this study is to evaluate, through NPV comparisons, different constrained scenarios, under geological uncertainty, determining the possibility of moving the constraints from their current position and/or defining priorities measuring the impact that each of them represents on the project's profitability. The methodology is applied to a phosphate mine, to determine the best alternative from a long-term mine planning perspective. The use of the hybrid pit approach, applied to a simulated grade model, allowed to identify the occurrence of probability zones within a mathematical pit, providing further information to support decision making regarding infrastructure relocation.
keywords:
mine planning; surface constraints; geological uncertainty; NPV; pit optimization
1. Introduction
Mining operations demand extensive studies regarding technical and economic aspects. Decision making must be done after a comprehensive understanding of the geological, operational and economical parameters. However, even with a detailed study about those parameters, it might not be enough to precisely predict their behavior. Therefore, decisions on planning, especially long-term, carry a high degree of uncertainty (ALBACH, 1967ALBACH, H. Long range planning in open-pit mining. Management science. v. 13, n. 10, p. B-549-B-568, 1967.).
Risk assessment during the strategic planning plays a critical role in a mining project and must cover the variables with highest impact potential on project's final economical value (DIMITRAKOPOULOS; MARTINEZ; RAMAZAN, 2007DIMITRAKOPOULOS, R., MARTINEZ, L., RAMAZAN, S. A maximum upside / minimum downside approach to the traditional optimization of open pit mine design. Journal of mining science, v. 43, n. 1, p. 81-90, 2007.). Depending on variable fluctuations and their impact on the current mining scenario, the operation's feasibility might be put at risk (DEUTSCH; GONZÁLEZ; WILLIAMS, 2015DEUTSCH, M. V., GONZÁLEZ, E., WILLIAMS, M. Using simulation to quantify uncertainty in ultimate-pit limits and inform infrastructure placement. Mining engineering magazine, n. December, p. 49-55, 2015.; DIMITRAKOPOULOS; RAMAZAN, 2003DIMITRAKOPOULOS, R., RAMAZAN, S. Uncertainty-based production scheduling in open pit mining. Transactions of the Institutions of Mining and Metallurgy, Section a: Mining Technology, v. 316, n. 3, p. 106-112, 2003.; PERONI, 2002PERONI, R. L. Análise da sensibilidade do seqüenciamento de lavra em função da incerteza do modelo geológico. Porto Alegre: Universidade Federal do Rio Grande do Sul, 2002. (Thesis).).
Implementation of stochastic tools and processes to support strategic planning solutions is increasingly gathering attention within the mining community, as stated by Dagdelen (2001)DAGDELEN, K. Open pit optimization - strategies for improving economics of mining projects through mine planning. In: INTERNATIONAL MINING CONGRESS AND EXHIBITION OF TURKEY, 17. N. November, p. 117-122, 2001. and other authors who used such implementation to optimize pit limits (DEUTSCH, M.; DEUTSCH, C., 2013DEUTSCH, M. V., DEUTSCH, C. V. An open source 3d lerchs grossmann pit optimization algorithm to facilitate uncertainty management. CCG Annual Report 15, 2013. v. 2013, n. Line 6, p. 1-6.; ELKINGTON; DURHAM, 2011ELKINGTON, T., DURHAM, R. Integrated open pit pushback selection and production capacity optimization. Journal of mining science, v. 47, n. 2, p. 177-190, 2011.; LEITE; DIMITRAKOPOULOS, 2007LEITE, A., DIMITRAKOPOULOS, R. Stochastic optimisation model for open pit mine planning: application and risk analysis at copper deposit. Transactions of the Institutions of Mining and Metallurgy, Section a: Mining Technology, v. 116, n. 3, p. 109-118, 2007.), mine schedules (RAMAZAN; DIMITRAKOPOULOS, 2013RAMAZAN, S., DIMITRAKOPOULOS, R. Production scheduling with uncertain supply: a new solution to the open pit mining problem. Optimization and engineering, v. 14, n. 2, p. 361-380, 2013.), cut off calculation (LI; YANG; LU, 2012LI, S., YANG, C., LU, C. Cut-off grade optimization using stochastic programming in open-pit mining. In: INTERNATIONAL CONFERENCE ON INTERNET COMPUTING FOR SCIENCE AND ENGINEERING, 6. Proceedings... 2012. p. 66-69, 2012.) and stock sizes (VIANEN; OTTJES; LODEWIJKS, 2014VIANEN, T. VAN, OTTJES, J., LODEWIJKS, G. Simulation-based determination of the required stockyard size for dry bulk terminals. Simulation Modelling Practice and Theory, v. 42, p. 119-128, 2014.; WAQAR ALI ASAD; DIMITRAKOPOULOS, 2012WAQAR ALI ASAD, M., DIMITRAKOPOULOS, R. Optimal production scale of open pit mining operations with uncertain metal supply and long-term stockpiles. Resources Policy, v. 37, n. 1, p. 81-89, 2012.). Conventionally, such problems are treated with methods that generate results based on predetermined technical, economic and geologic parameters (LEITE; DIMITRAKOPOULOS, 2007LEITE, A., DIMITRAKOPOULOS, R. Stochastic optimisation model for open pit mine planning: application and risk analysis at copper deposit. Transactions of the Institutions of Mining and Metallurgy, Section a: Mining Technology, v. 116, n. 3, p. 109-118, 2007.), which end up restricting the planning to an alternative that is updated with the progress of the mining. However, the current reality of business presents complexity and dynamism, demanding that knowledge of uncertainties becomes a key part of strategic planning (SMITH, 2012SMITH, G. L. Strategic long term planning in mining. Journal of the Southern African Institute of Mining And Metallurgy, v. 112, n. 9, p. 761-774, 2012.).
Pit optimization is one of the most discussed and questioned topics in literature, along with mining sequencing. Several authors (e.g. DIMITRAKOPOULOS (1998)DIMITRAKOPOULOS, R. Conditional simulation algorithms for modelling orebody uncertainty in open pit optimisation. International journal of surface mining, reclamation and environment, v. 12, n. 4, p. 173-179, 1998., DIMITRAKOPOULOS; MARTINEZ; RAMAZAN (2007)DIMITRAKOPOULOS, R., MARTINEZ, L., RAMAZAN, S. A maximum upside / minimum downside approach to the traditional optimization of open pit mine design. Journal of mining science, v. 43, n. 1, p. 81-90, 2007.; HALL; STEWART (2004)HALL, B. E., STEWART, C. A. Optimising the strategic mine plan - methodologies, findings, successes and failures. Orebody modelling and strategic mine planning, v. 14, p. 301-307, 2004.) report some benefits of uncertainty model inclusion in optimal pit construction and interpretation, besides Deutsch, González and Williams (2015)DEUTSCH, M. V., GONZÁLEZ, E., WILLIAMS, M. Using simulation to quantify uncertainty in ultimate-pit limits and inform infrastructure placement. Mining engineering magazine, n. December, p. 49-55, 2015. highlight the importance of simulated models in decision making regarding infrastructure positioning, since it allows optimal pit variation range comprehension.
The optimal pit represents the reference for mid and short-term planners to set the mine schedule to the end of mine's life, thus the pit boundary will directly affect facility location, which should be placed in order to avoid blocking the geological resources, if future pit expansion becomes feasible in new favorable economic scenarios (DEUTSCH; GONZÁLEZ; WILLIAMS, 2015DEUTSCH, M. V., GONZÁLEZ, E., WILLIAMS, M. Using simulation to quantify uncertainty in ultimate-pit limits and inform infrastructure placement. Mining engineering magazine, n. December, p. 49-55, 2015.). Planning issues, such as infrastructure relocation might become usual problems in cases of complex orebodies and/or unstable prices that could directly affect pit dimensions and ore reserves.
In this perspective, this study presents a methodology that uses pit sensitivity analysis, under geological uncertainty and simulated grades, to support decision making concerning facility relocation, such as waste piles and support infrastructures (KUCKARTZ, 2017KUCKARTZ, B. T. Análise de expansão de cava com múltiplas restrições de superfície sob incerteza geológica. Porto Alegre: Universidade Federal do Rio Grande do Sul, 2017. (Master Dissertation).). By comparing the Net Present Value (NPV) of different possible relocation scenarios, it is possible to rank each situation from the highest to the least impacting constraint on the project's revenue, indicating the most attractive scenario for further mine development.
2. Methodology
Considering the multiple constraints that might exist in a project and also their combinations and interactions, ten different scenarios were considered in this study. The scenarios were proposed in order to reduce total possible scenarios (32 possibilities built with combinations of 5 different constraints) and yet to allow evaluation of each structure, even when combined with others. The first one is the unconstrained scenario, the second one considers keeping mining at its current situation (all constraints applied) to determine the maximum and minimum usage of mineral resources and perform the NPV assessment. The other eight scenarios are combinations of different configurations of constraint releases to calculate the impact that each infrastructure has on the project's result. Definition of each scenario considered previous knowledge from mine planning, regarding which structures are most likely to be moved. Slope stability angle, besides being an important constraint that would directly impact on NPV, was considered as used in the mine (54º global slope). The impact of such constraint variation, in the same mine, was described in Kuckartz, Peroni and Capponi (2017)KUCKARTZ, B. T., PERONI, R. L., CAPPONI, L. N. Mine planning under grade uncertainty and slope angle evaluation. 38th APCOM proceedings, p. 9-1 - 9-8, 2017..
For all scenarios, we generated optimized pits through the LG algorithm (LERCHS; GROSSMANN, 1965LERCHS, H., GROSSMANN, L. F. Optimum design of open-pit mines. Transactions, Canadian Mining and Metallurgical Bulletin, Montreal, Canada, v. LXVIII, p.17-24, 1965.) using a grade simulated model, built with the turning band method and 50 realizations. In the first phase, pit optimization was built using simulation E-Type, and NPV determined its maximum value for each optimized pit. After that, pits were ranked from the highest to the lowest NPV. In the second phase, for the best four NPV scenarios (plus scenario S1 - current situation), a hybrid pit methodology (WHITTLE; BOZORGEBRAHIMI, 2004WHITTLE, D., BOZORGEBRAHIMI, A. Hybrid pits - linking conditional simulation and lerchs-grossmann through set theory. Orebody Modelling and Strategic Mine Planning, v. 14, n. November, p. 22-24, 2004.) was applied to evaluate the uncertainty associated to grades in the areas where pit contours overlay surface constraints. Four occurrence probability values were chosen:
-
10% - The lowest chance of occurrence, which provides the largest pit influence zone. Outside this zone is a proper place to locate facilities; however, this might imply in higher operational costs;
-
50% - Delineates the average contour. This percentage was established to understand the pit contour behavior against grade variability;
-
80% - Pit with low uncertainty, considered with a good probability of occurrence and not as restrictive as a 100% occurrence probability.
-
100% - This scenario identifies the pit with the highest probability of occurrence, indicating where surface structures must not be placed. This scenario contains blocks that compose all 50 possible optimized pits, obtained using the simulated model.
A mine schedule was proposed for each one of the 80% scenarios, maximizing NPV and keeping the ore production and strip ratio (SR) constant. The final results, regarding NPV, were used to set up a final classification between scenarios.
3. Case study
To test the methodology, a case study was carried out in a pit excavated in a cylindrical shape orebody, composed of many different carbonatites, hosted in the surrounding barren volcanic rock, named Jacupiranguito. The processing plant produces three main products (phoscalcium, cement and magnesian) depending on the P2O5 and MgO grades. Table 1 shows the cutoffs for each element and the corresponding final products.
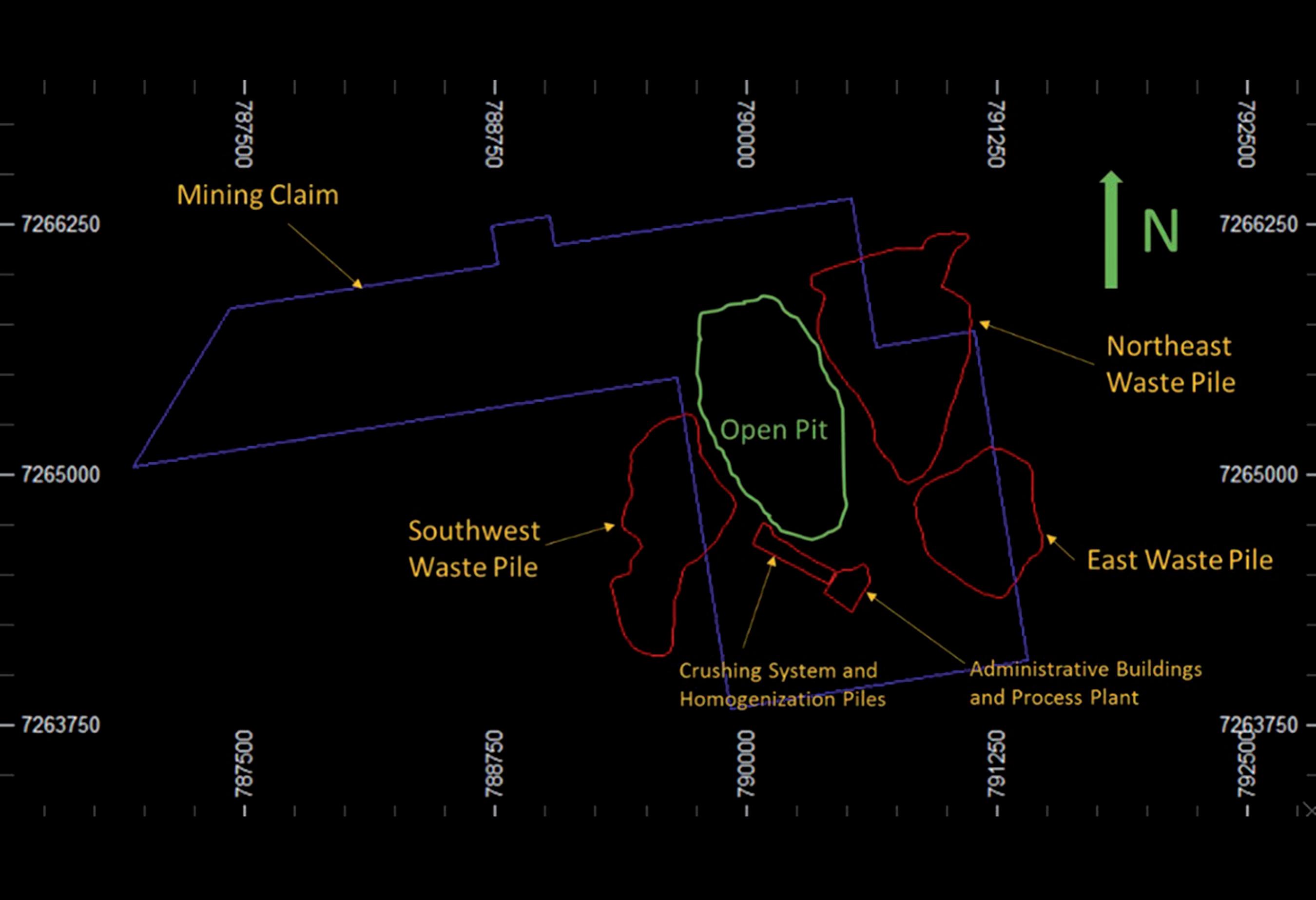
Several surface structures are surrounding the pit, limiting mine expansions. There are three waste dump piles blocking advances to the east, southeast and southwest directions. To the south, there are also two facility groups, one composed by the crushing system and homogenization piles, and the other one is represented by the processing plant and administrative buildings. In all situations, mining claim limit is always considered as a constraint. An overall view of the mine's current situation is shown in Figure 1.
Table 2 contains descriptions of all scenarios and some combinations of the six surface constraints as presented in Figure 1. (where blue line represents the mining claim limit, red lines the surface constraints and green line the current pit boundary). It is important to say that all scenarios consider the mining claim limit as a hard boundary for all the situations considered. Having said this, S0 would be the "unconstrained" case to serve as a reference for maximum outcome in terms of mineral resource usage, and consequently, creates the expectation of being able to be converted into ore reserves, if the limitations (or constraints) can be overcome.
4. Results and discussion
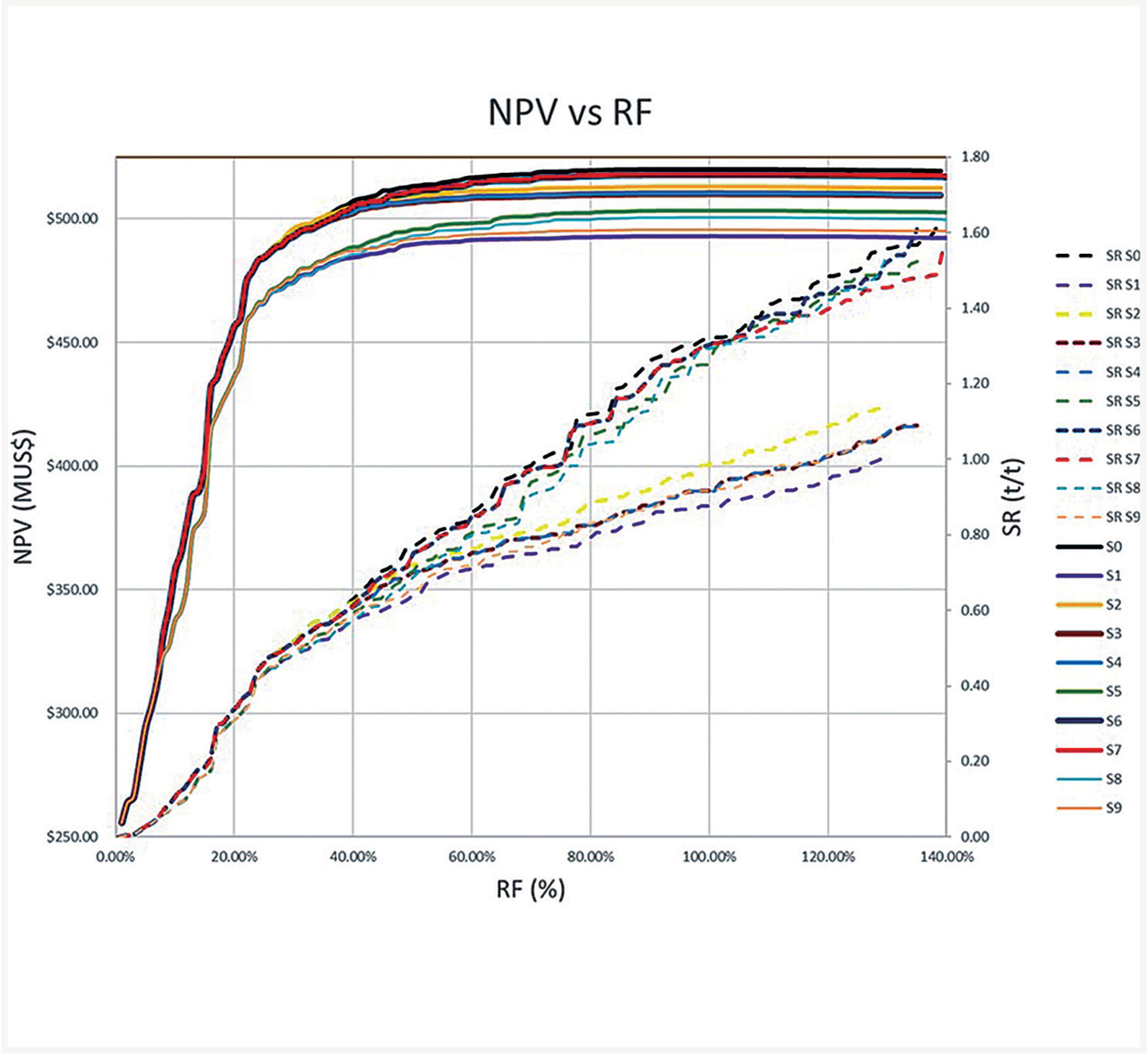
From the analysis of the ten scenarios tested using the proposed methodology, NPV and SR behavior are represented as the function of revenue factor (RF), as shown in Figure 2. Although there seems to occur a stabilization of the NPV curve around 100% revenue factor, what really happens is a discrete reduction of this value for all scenarios. This indicates that P2O5 selling price, has a small impact on NPV result. This behavior may be explained by the deposit's geometry, which is dependent on a large amount of waste material, increasing SR, to deepen the pit. Table 3 shows NPV results for each scenario with respective RF and mass content split in ore, waste and landfill material.
Graph of NPV (continuous lines) and SR (dashed lines) behavior as function of revenue factor resultant from LG optimization algorithm for each one of the ten scenarios
The S3 and S4 curves in Figure 2, (brown and light blue continuous lines, respectively) are identical for every RF. These two scenarios have the same constraints, apart from the processing plant and administrative buildings considered as constraints in S4. This is an evidence that this group of facilities is not actually blocking a significant amount of ore mass, expanding the pit over these facilities. This result is strengthened by pit contours from each scenario, as presented in Figure 3, where S3 and S4 are identical.
Optimized pit contours (yellow) obtained for each scenario compared to the surface constraints (red and blue). Grayish those constraints considered in each scenario
The same situation is observed with curves S6 and S7, in Figure 2, and indistinguishable pit contours in Figure 3. In this case, the only difference between these two scenarios is the E waste pile considered in S7, which is also not blocking pit expansion. Furthermore, as can be seen in Figure 3, both processing plant and administrative buildings and E pile are not constraints in all evaluated scenarios, as none pit contours intersect these structures lines.
All scenarios present similar NPV values, with the biggest difference found between S0 and S1 (S1 is 5.24% lower). As was expected, these scenarios represent the extreme NPV values (highest and lowest) as they are the unconstrained and most restrictive scenarios.
All scenarios, except S5 and S8, follow the same behavior demonstrating that the increase in total mass provides higher NPV. Scenarios S0, S5, S6, S7 and S8 contain the largest amounts of waste and landfill material, with around 43% higher than S1, S2, S3, S4 and S9. Total ore mass is also around 20% higher for these scenarios and the higher average grades of P2O5 are provided by S1, S2, S3 and S4. This result might be explained by the lower amount of waste content, but also by the releasing of the southern portion (crushing system and homogenization piles) where there is less waste material to be removed. Scenario S9, despite its low waste and landfill content, has similar P2O5 average grade to S5, which indicates that the crushing system and homogenization piles are blocking a phosphate high grade portion of the deposit.
The resultant optimal pit contours for each scenario is shown in Figure 3, where the yellow areas represent optimal pit contours and blue and red lines the mining claim limit and surface constraints, respectively.
The two more restrictive structures to pit expansion are the NE waste pile and crushing system plus homogenization piles. In all scenarios, except the ones where they are considered as constraints, the pit limits exceed their boundaries. Pit expansion to the southern portion is explained by the phoscalcium ore concentration, which results an average P2O5 grade of 5,86%, which is higher than other regions.
Table 4 shows total ore mass and the respective average grade that each surface structure is blocking. These results highlight the interference of crushing system and homogenization piles as the major constraint.
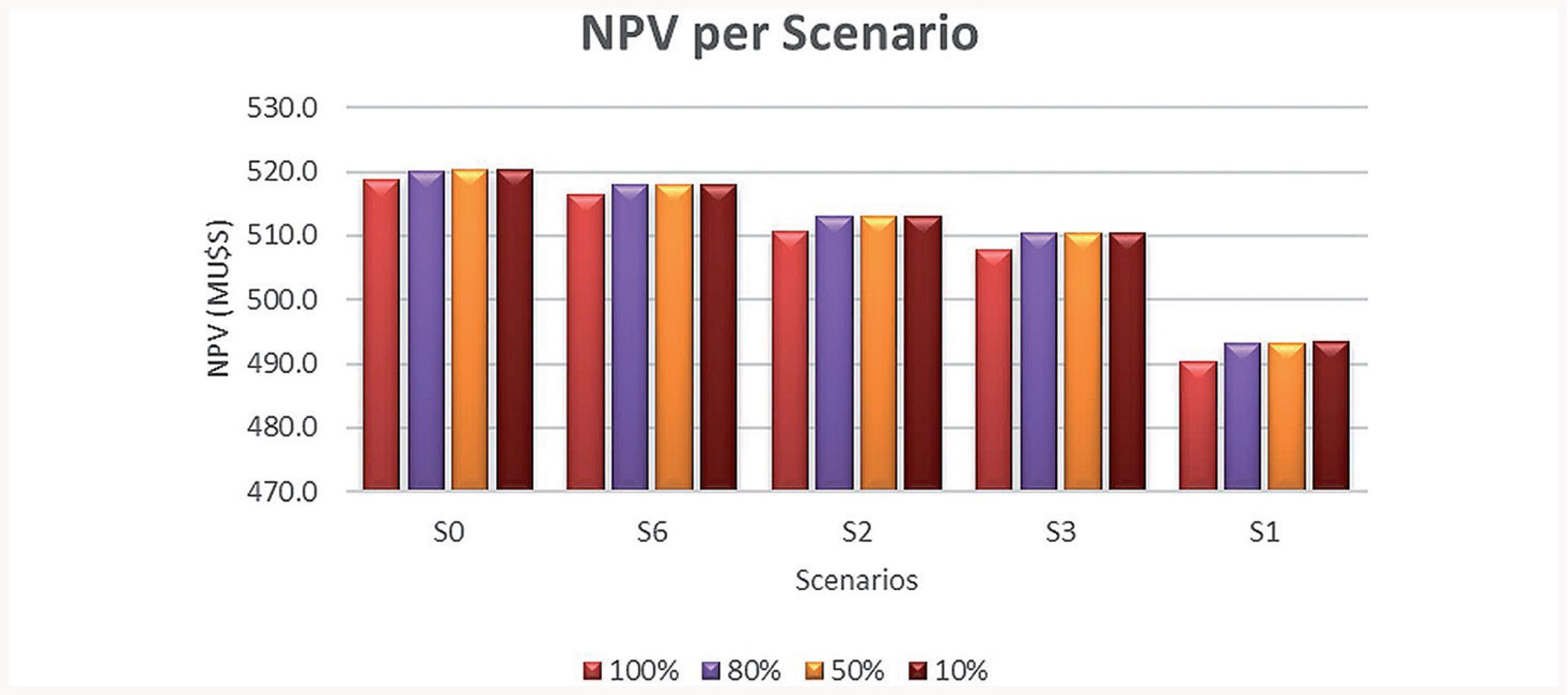
The four best scenarios to be used in the second phase analysis, according to the highest to lowest NPV, are S0, S6, S2 and S3 (S1 is also included as reference). The Geological Risk Assessment (GeoRisk) tool, from NPV Scheduler software, was used to generate probability occurrence pits of 100%, 80%, 50% and 10%.
NPV results for each scenario and occurrence probability can be seen in Figure 4. The results are very similar among probability pits for each scenario. The greater difference in all scenarios lies between 100% and 80%, thus, it is indicated that the geological variability, regarding P2O5 grades, is not large enough to generate different pits.
To illustrate the low pit variability, Figure 5 presents the contours of pits with 100%, 80%, 50% and 10% occurrence probability. Small differences between probability pit outlines, for all five scenarios are observed, especially between 80%, 50% and 10%, which reinforces low data variability. Pit outlines of 50% and 10% are virtually identical, except for a few sectors. In some areas, where divergences between pit limits are bigger, the sector was highlighted. Even in those areas, it is hard to identify detachment between pit limits of 80% and 10% (which is very similar to the 50% pit). The small variation observed is attributed to the orebody geometry that is cylindrical, vertical and centralized within the pit.
After the risk analysis, the scheduling process was carried out, assuming the 80% probability pit of the five considered scenarios, to determine the final ranking. The scheduling was performed according to actual mine production and also trying to stabilize the yearly stripping ratio and feed grades. Table 5 shows the results obtained after sequencing the scenarios, the results from S1 pit are used as reference and comparison in case no physical constraint is released and consequently no relocation will be done.
Scenario S0 demonstrated to be the worst case after scheduling, with NPV reduction of about 21.26%. Scenario S6 is also bad, dropping the NPV value to 18.18%. This situation was expected due the high SR of these two scenarios, implying relocation of approximately 9 Mt of landfill in the first 10 years, if compared to other scenarios.
Scenario S2 became the most attractive solution at this point, presenting 8.9% NPV increase compared to S0. However, S3 has a very similar NPV value, and still needs to relocate 12 Mt less landfill compared to S2, representing an attractive alternative also.
5. Conclusion
The results obtained in this study show that the methodology presented herein is capable of offering a range of possibilities when analyzing multiple constraints besides ranking the alternatives and determining the impacts that each has on a project's viability. Insertion of uncertainty models demonstrated to be a useful tool to predict the relationship between orebody variability and the resultant optimum pit. Thereafter, the hybrid pit approach demonstrated to be an effective process to take into account simulated models and build the probability zones, which contain valuable information to analyze facility allocation, preventing interferences with pit expansions.
Considering the results obtained from the case study, some of these surface structures, such as the northeast waste pile, became an interesting alternative to increase the project's NPV when compared to the other constraints. The analysis demonstrated that moving the NE waste dump increases mineral resource usage, while on the other hand, the necessity of relocation in the first years penalizes NPV, considering the amount of additional waste to be moved. Other surface constraints like the eastern pile, processing plant and administrative buildings do not turn out to be constraints as, in all scenarios evaluated, the pit limits do not intersect them.
Moving the crushing + homogenization system and southwestern waste pile, according to the S2 scenario, is the best alternative as demonstrated in this study. However much of the resources will be left in place and a pit design would be necessary to determine the amount of ore that would be left behind before a final decision is taken.
Despite the low variability of pit limits, it was possible to identify some areas where surface structures should not be placed or moved in. Yet, the relevance of the necessity of available areas for waste relocation and/or waste removal must be considered in all scenarios.
It is also interesting to consider the possibility of transition for underground operation. Even moving surface structures some of the resource still might not be possible to reach with the deepest ultimate pit scenario.
References
- ALBACH, H. Long range planning in open-pit mining. Management science v. 13, n. 10, p. B-549-B-568, 1967.
- DAGDELEN, K. Open pit optimization - strategies for improving economics of mining projects through mine planning. In: INTERNATIONAL MINING CONGRESS AND EXHIBITION OF TURKEY, 17. N. November, p. 117-122, 2001.
- DEUTSCH, M. V., DEUTSCH, C. V. An open source 3d lerchs grossmann pit optimization algorithm to facilitate uncertainty management. CCG Annual Report 15, 2013. v. 2013, n. Line 6, p. 1-6.
- DEUTSCH, M. V., GONZÁLEZ, E., WILLIAMS, M. Using simulation to quantify uncertainty in ultimate-pit limits and inform infrastructure placement. Mining engineering magazine, n. December, p. 49-55, 2015.
- DIMITRAKOPOULOS, R. Conditional simulation algorithms for modelling orebody uncertainty in open pit optimisation. International journal of surface mining, reclamation and environment, v. 12, n. 4, p. 173-179, 1998.
- DIMITRAKOPOULOS, R., MARTINEZ, L., RAMAZAN, S. A maximum upside / minimum downside approach to the traditional optimization of open pit mine design. Journal of mining science, v. 43, n. 1, p. 81-90, 2007.
- DIMITRAKOPOULOS, R., RAMAZAN, S. Uncertainty-based production scheduling in open pit mining. Transactions of the Institutions of Mining and Metallurgy, Section a: Mining Technology, v. 316, n. 3, p. 106-112, 2003.
- ELKINGTON, T., DURHAM, R. Integrated open pit pushback selection and production capacity optimization. Journal of mining science, v. 47, n. 2, p. 177-190, 2011.
- HALL, B. E., STEWART, C. A. Optimising the strategic mine plan - methodologies, findings, successes and failures. Orebody modelling and strategic mine planning, v. 14, p. 301-307, 2004.
- KUCKARTZ, B. T. Análise de expansão de cava com múltiplas restrições de superfície sob incerteza geológica. Porto Alegre: Universidade Federal do Rio Grande do Sul, 2017. (Master Dissertation).
- KUCKARTZ, B. T., PERONI, R. L., CAPPONI, L. N. Mine planning under grade uncertainty and slope angle evaluation. 38th APCOM proceedings, p. 9-1 - 9-8, 2017.
- LEITE, A., DIMITRAKOPOULOS, R. Stochastic optimisation model for open pit mine planning: application and risk analysis at copper deposit. Transactions of the Institutions of Mining and Metallurgy, Section a: Mining Technology, v. 116, n. 3, p. 109-118, 2007.
- LERCHS, H., GROSSMANN, L. F. Optimum design of open-pit mines. Transactions, Canadian Mining and Metallurgical Bulletin, Montreal, Canada, v. LXVIII, p.17-24, 1965.
- LI, S., YANG, C., LU, C. Cut-off grade optimization using stochastic programming in open-pit mining. In: INTERNATIONAL CONFERENCE ON INTERNET COMPUTING FOR SCIENCE AND ENGINEERING, 6. Proceedings... 2012. p. 66-69, 2012.
- PERONI, R. L. Análise da sensibilidade do seqüenciamento de lavra em função da incerteza do modelo geológico Porto Alegre: Universidade Federal do Rio Grande do Sul, 2002. (Thesis).
- RAMAZAN, S., DIMITRAKOPOULOS, R. Production scheduling with uncertain supply: a new solution to the open pit mining problem. Optimization and engineering, v. 14, n. 2, p. 361-380, 2013.
- SMITH, G. L. Strategic long term planning in mining. Journal of the Southern African Institute of Mining And Metallurgy, v. 112, n. 9, p. 761-774, 2012.
- VIANEN, T. VAN, OTTJES, J., LODEWIJKS, G. Simulation-based determination of the required stockyard size for dry bulk terminals. Simulation Modelling Practice and Theory, v. 42, p. 119-128, 2014.
- WAQAR ALI ASAD, M., DIMITRAKOPOULOS, R. Optimal production scale of open pit mining operations with uncertain metal supply and long-term stockpiles. Resources Policy, v. 37, n. 1, p. 81-89, 2012.
- WHITTLE, D., BOZORGEBRAHIMI, A. Hybrid pits - linking conditional simulation and lerchs-grossmann through set theory. Orebody Modelling and Strategic Mine Planning, v. 14, n. November, p. 22-24, 2004.
Publication Dates
-
Publication in this collection
Apr-Jun 2019
History
-
Received
18 July 2018 -
Accepted
05 Nov 2018