Abstract
The objective of the present study is to evaluate the fluid dynamics of a flotation column (2" in diameter and 6 m in height) based on gas hold-up measurements and, in particular, by applying the liquid-phase RTD (residence time distribution) technique. Additionally, a comparative study is performed between different methodologies used to determine RTD hydrodynamic parameters such as fitting of tanks-in-series and axial dispersion models to the experimental data.
The evidence indicates that the axial dispersion and tanks-in-series models agreed well with the experimental data, with a slight advantage of the first model, in terms of obtaining the fluid dynamic parameters. It was proven that the axial dispersion model parameters (Pe or Nd) can be obtained with good precision (R2 > 0.99) within the evaluated ranges from correlations that use the number of tanks in series (N) values estimated by the tanks-in-series model.
keywords:
flotation column; fluid dynamics; residence time distribution
keywords:
flotation column; fluid dynamics; residence time distribution
1. Introduction
In many industrial processes, such as flotation, the equipment is continuously operated with at least one input and one output, through which matter and/or energy is transferred. Such processes are known as open systems. In the design of continuous equipment, the flow is often considered to be ideal, i.e., perfectly agitated or of the piston-flow type (Fogler, 1992FOGLER, H. S. Residence time distributions. In: FOGLER, H. S. Elements of chemical reaction engineering. 2nd ed. New Jersey: Prentice-Hall International, 1992.; Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.). However, flow through equipment does not always follow ideal patterns, which may generally interfere with system performances, which thus generates responses below what is expected.
The residence time distribution (RTD) theory was created by studying flow in real, continuous systems with the purpose of quantifying any deviations from ideal behaviour (Danckwerts, 1953DANCKWERTS, P. V. Continuous flow systems: distribution of residence times. Chemical Engineering Science, v. 2, p. 1-13, 1953.; Zwietering, 1959ZWIETERING, T. N. The degree of mixing in continuous systems. Chemical Engineering Science, v. 11, p. 1-15, 1959.). The RTD analysis represents a useful and valuable tool to estimate the mixing quality within equipment, including flotation cells. This technique uses a tracer element or marker, such as dye, inorganic salts, or activated radioactive elements, etc., inserted into the feed stream of cells or equipment, generally applied as a pulse, which is then used to analyse the concentration of the tracer in the output, as indicated in Figure 1 (Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366., Lima et al., 2005LIMA, O. A.; LEAL FILHO, L. S.; SILVA, A. L.; MOURA, A. J. Distribuição de tempos de residência da polpa em células mecânicas de flotação. REM: Rev. Esc. Minas,Ouro Preto, v. 58, n. 3, p. 213-218, 2005., Santos, 2005SANTOS, A. R. Estudo do comportamento dinâmico de colunas de flotação utilizando técnicas nucleares. 2005. 134 f. Dissertação (Mestrado em Ciência e Tecnologia das Radiações, Minerais e Materiais) - CDTN/CNEN, Belo Horizonte, 2005.).
Specifically in the case of a column flotation process, several advantages can be cited in relation to conventional cells, which lead to higher recovery when processing ore of finer grain sizes, particularly because of the better control of the size of the generated bubbles and the addition of wash water at the top of the column, which decreases the hydrodynamic entrainment of hydrophilic particles in the froth (Dobby and Finch, 1985DOBBY, G. S.; FINCH, J. A. Mixing characteristics of industrial flotation columns. Chemical Engineering Science, v. 40, n. 7, p. 1061-1068, 1985.; Mills et al., 1992MILLS, P. J. T.; O'CONNOR, C.T., The mixing characteristics of solid and liquid phases in a flotation column. Minerals Engineering, v. 5, n. 10-12, p. 1195-1205, 1992. ; Santos, 2005SANTOS, A. R. Estudo do comportamento dinâmico de colunas de flotação utilizando técnicas nucleares. 2005. 134 f. Dissertação (Mestrado em Ciência e Tecnologia das Radiações, Minerais e Materiais) - CDTN/CNEN, Belo Horizonte, 2005.).
Normally, industrial flotation columns are operated under pre-established operational conditions according to studies performed in pilot columns; conditions include the air flowrate, gas hold-up (volume fraction of air in the column), feed flowrate or superficial feed velocity, percentage of solids, reagent dosage, average residence time (Santos, 2005SANTOS, A. R. Estudo do comportamento dinâmico de colunas de flotação utilizando técnicas nucleares. 2005. 134 f. Dissertação (Mestrado em Ciência e Tecnologia das Radiações, Minerais e Materiais) - CDTN/CNEN, Belo Horizonte, 2005.). According to Mavros (1993MAVROS, P.; DANIILIDOU, A. Mixing in flotation columns. Part II. Liquid-phase residence time distributions studies. Minerals Engineering, v. 6, n. 7, p. 707-719, 1993.) and Santos (2005), the mixing condition in which the liquid, solid, and gas phases are found in the collection zone of a flotation column is a preponderant factor for process recovery. Additionally, according to these authors, the lower the turbulence in the collection zone, the better the performance of the column which is a primary factor that affects the collection and release of mineral particles by bubbles. Studies performed by Goodall and O'Connor (1992GOODALL, C. M.; O'CONNOR, C. T. Residence time distribution studies in a flotation column. Part 2: the relationship between solids residence time distribution and metallurgical performance. International Journal of Mineral Processing, v. 36, p. 219-228, 1992.) reported that the mixing intensity in the collection zone of the column only slightly influences the recovery of the flotation process of pyrite, which is explained by the use of a column height larger than necessary for the obtained results. Shukla et al. (2010SHUKLA, S. C.; KUNDU, G.; MUKHERJEE, D. Study of gas holdup and pressure characteristics in a column flotation cell using coal. Minerals Engineering, v. 23, n. 8, p. 636-642, 2010.) also agrees that a highly turbulent mixture in the collection zone affects bubble-particle adhesion, which consequently affects the flotation process. In this context, by knowing the distribution and average residence time of the present phases, the mixing intensity in the cell can be quantified and correlated to process recovery (Santos, 2005). When the phases are properly mixed, the occurrence of dead zones or short-circuits is minimised, offering more appropriate hydrodynamic conditions to achieve a better flotation performance. Additionally, the determination of the liquid-phase RTD parameters, which is assisted by fluid dynamics models that describe the mixing intensity within the flotation column, can be useful to establish the scale-up procedure of the equipment (Yianatos et al., 2017YIANATOS, J.; VINNETT, L.; PANIRE, I.; ALVAREZ-SILVA, M.; DÍAZ, F. Residence time distribution measurements and modelling in industrial flotation columns. Minerals Engineering, v.110, p. 139 - 144, 2017.).
A literature review on the application of the RTD technique in mechanical flotation cells and columns in the last decades was performed, as presented by Table 1. An analysis of this table indicates the existence of a relatively reasonable number of studies performed on the subject; however, few of them focus on a comparative analysis of the adequacy of the main models used: continuous stirred-tank reactor - CSTR in series (tanks-in-series model), and plug-flow reactor - PFR with axial dispersion (axial dispersion model). In the axial dispersion model, the mixture is generated by the deviation from an ideal PFR. The most commonly used tracer element detection techniques are the following: spectrophotometry for dyes, such as methylene blue and fluorescein (dye fluorescein); conductivity for KCl and NaCl (except in Lima et al. (2005LIMA, O. A.; LEAL FILHO, L. S.; SILVA, A. L.; MOURA, A. J. Distribuição de tempos de residência da polpa em células mecânicas de flotação. REM: Rev. Esc. Minas,Ouro Preto, v. 58, n. 3, p. 213-218, 2005.), where atomic absorption was used); pH measurements for HCl; and gamma-ray spectroscopy for radioactive tracers and irradiated elements.
In this sense, the present study is propitious because the efficiency of the flotation process is strongly affected by the fluid dynamics of the system. The purpose of the present study is to evaluate the fluid dynamics of a flotation column by performing liquid-phase RTD tests as a function of key process variables, which are the following: superficial velocity of feed and air, and froth concentration. A comparative study was performed between different methodologies used to determine the RTD hydrodynamic parameters, which include approximation by discrete systems and nonlinear fit of the tanks-in-series and axial dispersion models for the experimental data.
2. Materials and methods
2.1 Materials
A.R. grade potassium chloride (KCl, 74.55 g/mol) in solutions of 1 mol/L and methylene blue - MB (C16H18ClN3S.xH2O, 319.86.xH2O g/mol) in solutions of 3.13 x 10-3 mol/L; both chemical tracers were purchased from SIGMA ALDRICH®. Polyalkylene glycol ether-based Flotanol D25 from Clariant S. A. was used as the frother, in the different concentrations: 0; 2.5; 5.0, and 7.5 mg/L.
2.2 Experimental determination of the RTD
Determining the RTD consists of continuously operating the column with previously known air and water flowrates according to the conditions recommended in literature (Aquino et al., 2010AQUINO, J. A.; OLIVEIRA, M. L. M.; FERNANDES, M. D. Flotação em colunas. In: LUZ, A. B.; SAMPAIO, J. A.; FRANÇA, S. C. A. (ed.). Tratamento de minérios. 5 ed. Rio de Janeiro: CETEM/MCT, 2010. cap. 12, p. 517-556.; Finch and Dobby, 1990FINCH, J. A.; DOBBY, G. S. Column flotation. Oxford: Pergamon Press, 1990.). Once the desired conditions are established, an amount of tracer is instantaneously added to the column feed (impulse disturbance), and a chronometer is simultaneously activated. In predetermined time intervals, samples are collected in the output flow (tailings) to evaluate the tracer element concentration with time using the spectrophotometric analysis technique for dye or electric conductivity for inorganic salts. A volume of tracer sample of 66 mL was used for injection, which in comparison with column volume (13.200 ml) is negligible (0.5% of the volume of the column). The conductivity was measured with an MS Tecnopon (model mCA-150) conductometer, whereas the absorbance was measured by an HACH visible spectrophotometer, model DR5000, with a wavelength of 620 nm. The experiments were performed in the laboratory flotation column at the Centre for Mineral Technology (CETEM) with an internal diameter of 5.1 cm and height 600 cm, which was built from transparent PVC with a total volume of 14.3 L and manufactured by Eriez Minerals Flotation Group - Canada, Inc. (Figure 2). All experiments were conducted using a column height of 570 cm in the collection zone in the column (liquid-gas), with the first segment of the column, at the bottom (40 cm), of 7.6 cm in diameter, corresponding to 13.2 L of volume. Thus, 30 cm of froth layer height (below the overflow lip) was held in the experiments in which a frother was used. The experimental apparatus also comprises of a system to control the level, wash water, and air flowrates using rotameters and peristaltic pumps for the feed and product output (Cole-Parmer®, Model 7553-75).
2.3 Experimental determination of gas hold-up in the column
The air volume fraction in the column, which is known as gas hold-up (eg), was determined by the methodology of level or volume measurement with the aid of a calibrated scale fixed in the column, which is also known as the gas-liquid displacement method (overall hold-up). This method consists of adjusting the liquid and air flowrates in the column under continuous operation. After reaching steady-state operation, the air feed is instantaneously closed, and the liquid volume (VL) inside of the column is measured when all bubbles have been released (Finch and Dobby, 1991FINCH, J. A.; DOBBY, G. S. Column flotation: a selected review. Part I. International Journal of Mineral Processing,v. 33, n. 1, p. 343-354, 1991.). Thus, the gas hold-up in the column is calculated according to Equation (1). Since the gas hold-up in the froth zone is typically up to 90% (liquid hold-up less than 10%) in the flotation process (Finch and Dobby, 1990) and this froth layer represents only about 5% of the total volume of the column, the content of liquid in the froth zone was neglected to estimate the gas hold-up in the collection zone.
where VT represents the total volume in the collection zone in the column (liquid + gas).
2.4 Liquid-phase RTD in the flotation column
To dimension continuous systems, such as flotation cells, it is practical to use nominal residence time or spatial time (τ) of the system pulp, also known as theoretical residence time, which is defined by Equation (2).
where V is the column volume occupied by liquid phase, and Qf is the volumetric feed flowrate in the system input.
The flotation cells generally present a certain level of agitation and phase mixing, where the RTD analysis provides the average residence time (tm) that may differ greatly from the nominal residence time (τ). Only in the ideal situation, where the equipment is perfectly agitated, are these times equal (tm=τ). Therefore, the comparison of the average residence time and nominal residence time in the system makes it possible to verify if the flow is ideal (when τ=tm) or to identify the type of deviation from the ideal flow. If tm>τ, short-circuit is predominant, whereas tm<τ indicates the formation of dead zones in the equipment.
2.4.1 RTD by discrete systems
To investigate the fluid dynamics of the flotation column, the most commonly used feed disturbance is the impulse type (impulsional), where the concentration of the tracer is periodically monitored at the bottom output of the column. For this type of disturbance, the residence time distribution function E(τ), its average residence time tm and variance σt2 are given by Equations (3), (4), and (5) respectively, which are presented next (Fogler, 1992FOGLER, H. S. Residence time distributions. In: FOGLER, H. S. Elements of chemical reaction engineering. 2nd ed. New Jersey: Prentice-Hall International, 1992.; Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.; Melo, 2002MELO, M. V. Tratamento de águas oleosas por flotação. 2002. Tese (Doutorado em Engenharia Química) - COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 2002.). The variance of the distribution σ2 makes it possible to determine the dispersion of the distribution around its average value.
These parameters are experimentally determined by measuring the concentration of a tracer - c(τ) as a function of time - t, as the response to an applied impulse tracer concentration signal in the feed.
2.4.2 Tanks-in-series model
For N perfectly stirred and identical tanks in series, the distribution function is given by Equation (6), whereas the number of tanks in series is calculated by Equation (7) (Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.).
where G(N) is the gamma function.
Using dimensionless variables, where θ=t/tm and E(θ)=E(t)*tm, the experimental curve of E(θ) versus θ is obtained; thus, the tanks-in-series model in dimensionless variables becomes Equation (8) (Mavros et al., 1989MAVROS, P.; LAZARIDIS, N. K.; MATIS, K. A. A Study and Modelling of Liquid-Phase Mixing in a Flotation Column. International Journal of Mineral Processing, v. 26, p. 1-16, 1989.):
The variance for the dimensionless time (σθ2) can be obtained by Equation (7).
2.4.3 Axial dispersion model
This model considers that during transfer by convection, an axial dispersion phenomenon of the evaluated phase or element of interest (such as fluid molecules or solid or tracer particles) occurs along the system, which results in a certain mixing level. A balance of the element of interest (tracer for the present study) that is transported along a column of length Lc of the collection zone by convection and dispersion is represented by Equation (9). The extension of the collection zone is defined as the region of the column between the pulp/froth interface and the air sparger (Finch and Dobby, 1990FINCH, J. A.; DOBBY, G. S. Column flotation. Oxford: Pergamon Press, 1990.).
where c is the tracer concentration, u is the tracer flow velocity in the x axial direction (considered as the interstitial velocity of the liquid in the column), and D is the axial dispersion coefficient of the tracer in the column.
The dimensionless variables are defined
where Pe is a dimensionless number known as the Peclet number, which represents the ratio between the velocities of transport by convection and dispersion; thus, for extremely small Pe values (approaching zero), the transport by convection is greatly reduced, and the flow can be approximated to that of CSTR. In turn, if Pe is extremely large (approaching infinity), transport by dispersion is greatly reduced and the flow can be approximated to that of PFR. The flotation column is generally considered as a type of reactor with intermediary flow between the two previously cited extreme conditions (Mankosa et al., 1992MANKOSA, M. J.; LUTTRELL, G. H.; ADEL, G. T.; YOON, R. H., A study of axial mixing in column flotation. International Journal of Mineral Processing, v. 35, n. 1, p. 51-64, 1992.). Several studies in literature have used a dimensionless parameter, referred to as the "vessel dispersion number" (Nd), to quantify the intensity of the axial mixture in the equipment, which is equal to the inverse of the Peclet number and is as a function of the coefficient of axial dispersion (D), as presented in Equation (11) (Dobby and Finch, 1985DOBBY, G. S.; FINCH, J. A. Mixing characteristics of industrial flotation columns. Chemical Engineering Science, v. 40, n. 7, p. 1061-1068, 1985.; Ityokumbul et al., 1988ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Parameter estimation with simplified boundary conditions. Chemical Engineering Science, v. 43, n. 9, p. 2457-2462, 1988.; Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.).
The relationship between the interstitial (u) and superficial (uL) liquid velocity is given by Equation (12) being known the gas hold-up (εg) of the column for a given experimental condition. In mineral processing, the symbol Jf is more commonly used to represent the superficial velocity of the liquid in the feed, which is the same nomenclature used in the present study.
In contrast to the analysis of Pe, when Nd approaches zero, the dispersion is negligible, and the flow approaches that of PFR. In turn, when this parameter approaches infinity, the dispersion is extremely high, and the flow approaches that of CSTR. Thus, these parameters allow the evaluation of the mixture intensity of a given phase inside equipment, such as the flotation cells.
To solve Equations (9) and (10), the boundary conditions open to diffusion (known as open-open) and for Nd>0.01 were used, as presented in Equations (13) and (14) (Dobby and Finch, 1985DOBBY, G. S.; FINCH, J. A. Mixing characteristics of industrial flotation columns. Chemical Engineering Science, v. 40, n. 7, p. 1061-1068, 1985.; Ityokumbul et al., 1988ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Parameter estimation with simplified boundary conditions. Chemical Engineering Science, v. 43, n. 9, p. 2457-2462, 1988.; Levenspiel, 1999LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.). As it will later be demonstrated, the obtained Nd values were within the recommended range of application for the adopted model.
The variance for the axial dispersion model using the open-open boundary condition can be calculated with Equation (15).
3. Results and discussion
The results of the gas hold-up (εg) in the column are presented in Figure 3 (a) as a function of the superficial air velocity (Jg) for different concentrations of Flotanol D25. The superficial air velocity, as well as for the other flows, is defined by the ratio between the air volumetric flowrate and the cross-sectional area of the column (Finch and Dobby, 1991FINCH, J. A.; DOBBY, G. S. Column flotation: a selected review. Part I. International Journal of Mineral Processing,v. 33, n. 1, p. 343-354, 1991.).
(a) Gas hold-up as a function of the superficial air velocity for different concentrations of the Flotanol D25 frother and (b) surface tension as a function of the Flotanol concentration.
Figure 3(a) indicates an almost linear increase of the gas hold-up as the superficial air velocity increases as a function of the increased number of bubbles for higher air flowrates, which further increase when the frother concentration is increased. This result can be justified by the reduction of the surface tension (γ) of the Flotanol solution in the studied interval, as observed in Figure 3 (b), which minimises the coalescence of bubbles as a function of the orientation of the frother molecules at the surface of the bubbles (gas-liquid interface) according to various studies in literature (Finch and Dobby, 1990FINCH, J. A.; DOBBY, G. S. Column flotation. Oxford: Pergamon Press, 1990., Ityokumbul el al., 1995ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Effect of fine solids and frother on gas hold-up and liquid mixing in a flotation column. Minerals Engineering, v. 8, n. 11, p. 1369-1380, 1995., Couto et al., 2009COUTO, H. J. B.; NUNES, D.; NEUMANN, R.; FRANCA, S. C. A. Micro-bubble size distribution measurements by laser diffraction technique. Minerals Engineering., v. 22, n. 4, p. 330-335, 2009.).
The first experiments were performed using two types of chemical tracers for the liquid phase (MB and KCl), for comparison and selection purposes in the subsequent tests. As such, the superficial feed velocity (Jf) of the column was initially evaluated for a nominal residence time between 10 and 20 min, which is commonly used in column flotation processes. The experimental results of the residence time distribution E(τ) with time (τ), which was obtained by Equation (3) for the KCl tracer, are presented in Figure 4 (a) and for the dimensionless form in Figure 4 (b). Figures 4 (c) and (d) present the results for the MB tracer. The calibration curves obtained between the measurements of KCl concentrations with electric conductivity and concentration of MB with absorbance resulted in a correlation coefficient (R2) of the lines with values of 0.999 and 0.998, respectively.
(a) and (c) RTB function of superficial feed velocity (Jf) with time for KCl and MB, respectively; (b) and (d) in dimensionless variables (Jg=1.5 cm/s; Cf = 0 mg/L) for KCl and MB.
The tendency of the RTD curves was extremely similar for both tracers; thus, KCl was chosen for the other tests because, in addition to being used more often in literature, it is more chemically stable than MB, which presents photosensitive characteristics. Nevertheless, problems regarding the excessive adsorption of methylene blue have been previously reported in literature when it was used with solids (Dobby and Finch, 1985DOBBY, G. S.; FINCH, J. A. Mixing characteristics of industrial flotation columns. Chemical Engineering Science, v. 40, n. 7, p. 1061-1068, 1985.). The advantage of the latter is the visual perception of the variation of the tracer concentration by the colour variation of the solution inside of the column.
Equations (4), (5), and (7) were used to calculate the hydrodynamic parameters tm, σθ2, and N for discrete systems for several key process variables, which are presented in Table 2. When not evaluated, the adopted base conditions, i.e., fixed conditions, were (Jg=1.5; Jf=0.62) cm/s and Cf = 0 mg/L.
One of the advantages of determining the hydrodynamic parameters (tm and N) by discrete systems is the possibility of using them as initial values to adjust the tanks-in-series model, which increases the success of convergence and decreases the number of iterations required to obtain the adjusted parameters. For the axial dispersion model, the initial estimation of the Peclet number can be obtained using the variance calculated by the discrete system in Equation (15).
Table 3 presents the results of the parameters estimated by the tank-in-series and axial dispersion models by Equations (6) and (13), respectively, as well as the obtained correlation coefficients (R2). The parameters of the models were estimated by nonlinear regression of the experimental data using the least square method using STATISTICA 12 (StatSoft, Inc., 2013) software. The estimations of the fluid dynamic parameters for the two models were performed successfully, with a slight advantage to the axial dispersion model, which provided slightly higher correlation coefficients compared with those of the tanks-in-series model.
Several studies (Xu and Finch, 1991XU, M.; FINCH, J. A. The axial dispersion model in flotation column studies. Minerals Engineering, v. 4, p. 553-562, 1991.; Finch and Dobby, 1991) have compared values of Nd (Nd=1/Pe) obtained from open-open and closed-closed boundary conditions (Nd-oo and Nd-cc, respectively) for the same set of RTD data by adjusting it to the axial dispersion model using the method of least squares in both cases. It was demonstrated that for values of Nd lower than 0.5, particularly for values lower than 0.25, i.e., for the situation of the present study, the values obtained for both boundary conditions are extremely similar and optimally adjusted to the experimental data. In this context, the use of the open-open boundary condition presents a great advantage of simplicity in estimating Nd and can be obtained by the analytical solution according to Equation (13). This is different from using the closed-closed boundary condition normally performed in numerical methods, which requires more time and computational effort. Nonetheless and if necessary, the values of Nd-cc can be obtained from the values of Nd-oo by the correlation proposed by Ityokumbul et al. (1988ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Parameter estimation with simplified boundary conditions. Chemical Engineering Science, v. 43, n. 9, p. 2457-2462, 1988.), which results in relative precision (Xu and Finch, 1991). Nevertheless, although it was previously reported in literature that the open-open boundary condition for the axial dispersion model should only be used for Pe values greater than approximately 16 (Mavros, 1993MAVROS, P.; DANIILIDOU, A. Mixing in flotation columns. Part II. Liquid-phase residence time distributions studies. Minerals Engineering, v. 6, n. 7, p. 707-719, 1993.; Mavros, 1992), a good fit was obtained in the present study (with a correlation coefficient R2 greater than 0.99) for Pe values below this value. The estimated Pe values were in the range of 3 to 25. However, the obtained good fitting in all Pe range does not necessarily mean that the model has a physical meaning; it can be attributed to the proper structure of this model to fit the data.
Figure 5 presents the fitted results for both models with the experimental data for two different superficial feed velocity scenarios, denoted E2 (Jf = 0.93 cm/s) and E15 (Jf = 0.46 cm/s), in accordance with Table 2 using KCl as the tracer. The other experimental conditions used in these tests were Jg=1.5 cm/s; and Cf = 0 mg/L. In order to evaluate the errors of the experimental data from RTD measurements, the E2 assay was repeated three times. The error bars present in the experimental data from Figure 5 were calculated as twice the standard deviation from the triplicate measurements, considering a 95% confidence level. Since the experimental error values for assay E2 were low, the same level of errors was attributed for all assays, including E15. A slightly higher precision can be observed for the axial dispersion model, particularly at the extreme data points of the curve, i.e., the ascent and descent regions of the function.
Adjustment of the tanks-in-series and axial dispersion models to the experimental data of E2 (Jf = 0.93 cm/s) and E15 (Jf = 0.46 cm/s) tests using the KCl tracer.
Figure 6 presents the average residence time (tm) values obtained by discrete systems and the tanks-in-series and axial dispersion models as well as the corresponding spatial time as a function of superficial feed velocity.
Average residence times obtained from discrete systems and the tanks-in-series and axial dispersion models (Jg=1.5 cm/s; Cf = 0 mg/L).
As expected, the average residence time decreased as the superficial feed velocity increased, which was caused by the increase in the feed flowrate for a fixed volume in the column. The average residence times obtained by discrete systems and for both models presented similar results, in most cases, below the spatial time (τ) due to the previously explained reasons, which are related to the regions of lower mixing intensity in the column or stagnation zones.
Figure 7 presents the results of parameters for the models used, number of tanks-in-series (N), and Peclet number (Pe) in (a) and the column dispersion number (Nd) in (b) as a function of the superficial feed velocity for both tracers evaluated.
(a) Number of tanks-in-series (N) and Pe number and (b) N and column dispersion number (Nd) as a function of superficial feed velocity for both tracers KCl and MB.
The same behaviour was observed for both tracers, where the number of tanks-in-series (N) and Peclet number (Pe) increased, whereas the column dispersion number (Nd) decreased with an increase in the superficial feed velocity, which was also evidenced by the previously presented RTD curve of Figure 4. These results (lower Nd and higher N and Pe) indicate the decrease of mixing intensity inside the column, which is caused by the increase in Jf, and corroborated by many studies in literature (Mavros et al. 1989MAVROS, P.; LAZARIDIS, N. K.; MATIS, K. A. A Study and Modelling of Liquid-Phase Mixing in a Flotation Column. International Journal of Mineral Processing, v. 26, p. 1-16, 1989.; Mankosa et al., 1992MANKOSA, M. J.; LUTTRELL, G. H.; ADEL, G. T.; YOON, R. H., A study of axial mixing in column flotation. International Journal of Mineral Processing, v. 35, n. 1, p. 51-64, 1992.; Mavros and Danilidou 1993; Moustiri et al., 2001MOUSTIRI, S.; HEBRARD, G.; THAKRE, S. S.; ROUSTAN, M. A unified correlation for predicting liquid axial dispersion coefficient in bubble columns. Chemical Engineering Science, v.56, p. 1041-1047, 2001.; Shukla et al, 2010SHUKLA, S. C.; KUNDU, G.; MUKHERJEE, D. Study of gas holdup and pressure characteristics in a column flotation cell using coal. Minerals Engineering, v. 23, n. 8, p. 636-642, 2010.), but diverge from the results found by other authors (Goodall and O'Connor, 1991GOODALL, C. M.; O'CONNOR, C. T. Residence time distribution studies in a flotation column. Part l: The modelling of residence time distributions in a laboratory column flotation cell. International Journal of Mineral Processing, v. 31, p. 97-113, 1991. and 1992). In gas-liquid flotation columns, the most accepted conclusion in literature is that the increase of the superficial feed velocity, which increases the interstitial liquid velocity in the axial direction of the column according to Equation (12), causes less disturbance in the ascending gas flow, and therefore, there is less turbulence in the column and approaches the behaviour of the PFR reactor more (Mavros et al., 1989; Shukla et al., 2010). However, the fact that the column used in the present study presents a large length/diameter ratio (L/D~110), favouring the plug-flow condition (Mankosa et al., 1992). Additionally, it can be said that the KCl dispersion or mixing degree is slightly higher than that of MB, which may be due to the difference of size of the KCl and MB ions because the same concentrations of these tracers were used in the solutions. Since both the tracers are present as ions in aqueous solution (K+ and Cl- for KCl; C16H18N3S+ and Cl- for MB), another possibility for the differences between the two tracers may be due to the differences in the bubble size caused by the presence of these ions in the solution. Thus, changing the gas hold-up in the collection zone, may affect the liquid RTD in the column.
Figures 8 (a) and 8 (b) present the trends of the fluid dynamic parameters N and Nd with increases of the superficial air velocity (Jg) and frother concentration (Cf), respectively, using the KCl tracer. As observed in Figure 8 (b), the increase in frother concentration increased the degree of mixing inside of the column. The presence of the frother caused a greater dispersion of the liquid phase in the column compared with that at the condition without the frother, but maintained practically constant N and Nd levels in the studied Flotanol concentration range. The explanation is that the presence of the frother reduces the bubble size, which increases the air volume fraction (gas hold-up) caused by the increase in the number of bubbles per unit volume in the column. The increase in the superficial air velocity in the evaluated range (Figure 8 (a)) increased the mixing intensity of the liquid phase in the column, which has been observed by other authors (Mavros and Danilidou, 1993MAVROS, P.; DANIILIDOU, A. Mixing in flotation columns. Part II. Liquid-phase residence time distributions studies. Minerals Engineering, v. 6, n. 7, p. 707-719, 1993.; Massinaei et al., 2007MASSINAEI, M.; KOLAHDOOZAN, M.; NOAPARAST, M.; OLIAZADEH, M.; SAHAFIPOUR, M.; FINCH, J. A. Mixing characteristics of industrial columns in rougher circuit. Minerals Engineering, v. 20, p. 1360-1367, 2007.; Goodall & O'Connor, 1991GOODALL, C. M.; O'CONNOR, C. T. Residence time distribution studies in a flotation column. Part l: The modelling of residence time distributions in a laboratory column flotation cell. International Journal of Mineral Processing, v. 31, p. 97-113, 1991.; Mavros et al., 1989; Shukla et al., 2010SHUKLA, S. C.; KUNDU, G.; MUKHERJEE, D. Study of gas holdup and pressure characteristics in a column flotation cell using coal. Minerals Engineering, v. 23, n. 8, p. 636-642, 2010.), which is also explained by the increase in the number of bubbles in the column per volume unit. The decrease in N (higher mixing intensity) with increases in Jg was also observed by Goodall & O'Connor (1991) using a bench flotation column and radioactive tracer for the solid phase.
(a) N and Nd parameters as a function of the superficial air velocity (Cf = 0 mg/L) and (b) as a function of the frother concentration (Jg=1.5 cm/s), respectively. (Jf = 0.62 cm/s).
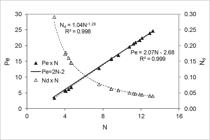
It is also important to comment that an increase in the frother concentration causes an increase in gas hold-up, which consequently increases the interstitial liquid velocity, according to Equation 12, leading to an increase in transport by convection. This occurs even for a fixed superficial liquid velocity in the column. Correlations between the parameters of the axial dispersion model (Pe and Nd) and the tanks-in-series model parameter (N) were obtained for all the evaluated experimental conditions, as presented in Figure 9. Additionally, the equation proposed by Elgeti (1996ELGETI, K. A new equation for correlating a pipe flow reactor with a cascade of mixed reactors. Chemical Engineering Science, v. 51, n. 23, p. 5077-5080, 1996.), to verify if these two models are equivalent, was plotted in Figure 9. This equation considers the Bodenstein number (Bo) as the Peclet number, as follows: .
Correlations between parameters Pe and Nd (axial dispersion model) as a function of N (tanks-in-series model).
From these correlations (linear for Pe versus N and power for Nd versus N), the parameters of the dispersion model can be obtained with great precision (R2 > 0.99) within the studied intervals using the N values estimated for the tanks-in-series model. It can also be seen that the Elgeti's equation had a good agreement with the experimental data (Pe versus N), mainly for N greater than 8. Special attention is drawn to the fact that this liquid-phase RTD study can be applied to the solid phase when it is composed of fine particles because, in this case, the differences of flow between these phases are small (Yianatos et al., 2001YIANATOS, J.; BERGH, L.; CONDORI, P.; AGUILERA, J. Hydrodynamic and metallurgical characterization of industrial flotation banks for control purposes. Minerals Engineering, v. 14, n.9, p. 1033-1046, 2001.; Yianatos et al., 2015). However, in RTD studies involving mineral pulps constituted by a significant amount of coarser particles (mainly > 150 µm), specific tests using proper tracers for the solid phase should be performed to obtain better results (Yianatos et al., 2001).
The RTD technique proved to be extremely useful and effective for the fluid dynamic study of the flotation column used in the experiments, which allows the evaluation of the mixing quality and flow type for different process variables.
4. Conclusions
The results show that the axial dispersion and tanks-in-series models agreed well with the experimental data, with a slight advantage for the first model, to obtain the fluid dynamic parameters. This fact might be related to the geometry of the column used, the large length/diameter (L/D) ratio, and more favourable plug flow, which thus demonstrates that this variable is extremely important to the flotation process in columns. It was proven that the parameters of the axial dispersion model (Pe/Nd) can be obtained with good precision (R2 > 0.99) and within the evaluated ranges from correlations using the N values estimated by the tanks-in-series model.
It was observed that the increase of superficial air velocity and frother concentration increased the mixing intensity of the liquid phase inside the column, whereas the superficial feed velocity had the opposite effect, according to the values of the fluid dynamic parameters determined.
Acknowledgements
The authors would like to thank the Brazilian Funding Research Agency (CNPq) for financial support and CETEM for the facilities and technical support.
References
- AQUINO, J. A.; OLIVEIRA, M. L. M.; FERNANDES, M. D. Flotação em colunas. In: LUZ, A. B.; SAMPAIO, J. A.; FRANÇA, S. C. A. (ed.). Tratamento de minérios 5 ed. Rio de Janeiro: CETEM/MCT, 2010. cap. 12, p. 517-556.
- CHEGENI, M. H.; ABDOLLAHY, M.; KHALESI, M. R. Column flotation cell design by drift flux and axial dispersion models. International Journal of Mineral Processing, v. 145, p. 83-86, 2015.
- COUTO, H. J. B.; NUNES, D.; NEUMANN, R.; FRANCA, S. C. A. Micro-bubble size distribution measurements by laser diffraction technique. Minerals Engineering, v. 22, n. 4, p. 330-335, 2009.
- DANCKWERTS, P. V. Continuous flow systems: distribution of residence times. Chemical Engineering Science, v. 2, p. 1-13, 1953.
- DOBBY, G. S.; FINCH, J. A. Mixing characteristics of industrial flotation columns. Chemical Engineering Science, v. 40, n. 7, p. 1061-1068, 1985.
- ELGETI, K. A new equation for correlating a pipe flow reactor with a cascade of mixed reactors. Chemical Engineering Science, v. 51, n. 23, p. 5077-5080, 1996.
- FINCH, J. A.; DOBBY, G. S. Column flotation Oxford: Pergamon Press, 1990.
- FINCH, J. A.; DOBBY, G. S. Column flotation: a selected review. Part I. International Journal of Mineral Processing,v. 33, n. 1, p. 343-354, 1991.
- FOGLER, H. S. Residence time distributions. In: FOGLER, H. S. Elements of chemical reaction engineering 2nd ed. New Jersey: Prentice-Hall International, 1992.
- GOODALL, C. M.; O'CONNOR, C. T. Residence time distribution studies in a flotation column. Part l: The modelling of residence time distributions in a laboratory column flotation cell. International Journal of Mineral Processing, v. 31, p. 97-113, 1991.
- GOODALL, C. M.; O'CONNOR, C. T. Residence time distribution studies in a flotation column. Part 2: the relationship between solids residence time distribution and metallurgical performance. International Journal of Mineral Processing, v. 36, p. 219-228, 1992.
- ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Parameter estimation with simplified boundary conditions. Chemical Engineering Science, v. 43, n. 9, p. 2457-2462, 1988.
- ITYOKUMBUL, M.T.; KOSARIC, N.; BULANI, W. Gas hold-up and liquid mixing at low and intermediate gas velocities I. Air-water system. Chemical Engineering Journal, v. 53, n.3, p. 167-172, 1994.
- ITYOKUMBUL, M. T.; KOSARIC, N.; BULANI, W. Effect of fine solids and frother on gas hold-up and liquid mixing in a flotation column. Minerals Engineering, v. 8, n. 11, p. 1369-1380, 1995.
- LELINSKI, D.; ALLEN, J.; REDDEN, L.; WEBER, A. Analysis of the residence time distribution in large flotation machines. Minerals Engineering, v. 15, p. 499-505, 2002.
- LEVENSPIEL, O. Part II: Flow patterns, contacting, and non-ideal flow. In: LEVENSPIEL, O. Chemical reaction engineering. 3rd ed. [S. l.]: John Wiley & Sons, 1999. p. 257-366.
- LIMA, O. A.; LEAL FILHO, L. S.; SILVA, A. L.; MOURA, A. J. Distribuição de tempos de residência da polpa em células mecânicas de flotação. REM: Rev. Esc. Minas,Ouro Preto, v. 58, n. 3, p. 213-218, 2005.
- MANKOSA, M. J.; LUTTRELL, G. H.; ADEL, G. T.; YOON, R. H., A study of axial mixing in column flotation. International Journal of Mineral Processing, v. 35, n. 1, p. 51-64, 1992.
- MASSINAEI, M.; KOLAHDOOZAN, M.; NOAPARAST, M.; OLIAZADEH, M.; SAHAFIPOUR, M.; FINCH, J. A. Mixing characteristics of industrial columns in rougher circuit. Minerals Engineering, v. 20, p. 1360-1367, 2007.
- MAVROS, P. Technical note validity and limitations of the closed-vessel analytical solution to the axial dispersion model. Minerals Engineering, v. 5, n. 9, p. 1053-1060, 1992.
- MAVROS, P. Mixing in flotation columns. Part I: Axial dispersion modelling. Minerals Engineering, v. 6, n. 5, p. 465-478, 1993.
- MAVROS, P.; LAZARIDIS, N. K.; MATIS, K. A. A Study and Modelling of Liquid-Phase Mixing in a Flotation Column. International Journal of Mineral Processing, v. 26, p. 1-16, 1989.
- MAVROS, P.; DANIILIDOU, A. Mixing in flotation columns. Part II. Liquid-phase residence time distributions studies. Minerals Engineering, v. 6, n. 7, p. 707-719, 1993.
- MELO, M. V. Tratamento de águas oleosas por flotação 2002. Tese (Doutorado em Engenharia Química) - COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 2002.
- MILLS, P. J. T.; O'CONNOR, C. T. The modelling of liquid and solids mixing in a flotation column. Minerals Engineering, v. 3, n. 6, p. 567-576, 1990.
- MILLS, P. J. T.; O'CONNOR, C.T., The mixing characteristics of solid and liquid phases in a flotation column. Minerals Engineering, v. 5, n. 10-12, p. 1195-1205, 1992.
- MOUSTIRI, S.; HEBRARD, G.; THAKRE, S. S.; ROUSTAN, M. A unified correlation for predicting liquid axial dispersion coefficient in bubble columns. Chemical Engineering Science, v.56, p. 1041-1047, 2001.
- PUGET, F. P.; MELO, M. V.; MASSARANI, G. Modelling of the dispersed air flotation process applied to dairy wastewater treatment. Brazilian Journal of Chemical Engineering, v. 21, n. 2, p.229-237, 2004.
- RICE, R. G.; OLIVER, A. D.; NEWMAN, J. P.; WILES, R. J. Reduced dispersion using baffles in column flotation. Powder Technology,v. 10, n. 4, p. 201-210, 1974.
- SANTOS, A. R. Estudo do comportamento dinâmico de colunas de flotação utilizando técnicas nucleares 2005. 134 f. Dissertação (Mestrado em Ciência e Tecnologia das Radiações, Minerais e Materiais) - CDTN/CNEN, Belo Horizonte, 2005.
- SHUKLA, S. C.; KUNDU, G.; MUKHERJEE, D. Study of gas holdup and pressure characteristics in a column flotation cell using coal. Minerals Engineering, v. 23, n. 8, p. 636-642, 2010.
- STATSOFT. Statistica Version 12. [S. l.]: StatSoft, 2013.
- XU, M.; FINCH, J. A. The axial dispersion model in flotation column studies. Minerals Engineering, v. 4, p. 553-562, 1991.
- XU, M.; FINCH, J. A. Solids mixing in the collection zone of flotation columns. Minerals Engineering, v. 5, n. 9, p. 1029-1039, 1992.
- YIANATOS, J.; BERGH, L.; CONDORI, P.; AGUILERA, J. Hydrodynamic and metallurgical characterization of industrial flotation banks for control purposes. Minerals Engineering, v. 14, n.9, p. 1033-1046, 2001.
- YIANATOS, J.; BERGH, L.; PINO, C.; VINNETT, L.; MUÑOZ, C.; YAÑEZ, A. Industrial evaluation of a new flotation mechanism for large flotation. Minerals Engineering, v. 36-38, p. 262 - 271, 2012.
- YIANATOS, J.; BERGH, C.; VINNETT, L.; PANIRE, I.; DÍAZ, F. Modelling of residence time distribution of liquid and solid in mechanical flotation cells. Minerals Engineering, v. 78, p. 69 - 73, 2015.
- YIANATOS, J.; CONTRERAS, F.; DÍAZ, F. Gas holdup and RTD measurement in an industrial flotation cell. Minerals Engineering, v. 23, p. 125 - 130, 2010.
- YIANATOS, J.; VINNETT, L.; PANIRE, I.; ALVAREZ-SILVA, M.; DÍAZ, F. Residence time distribution measurements and modelling in industrial flotation columns. Minerals Engineering, v.110, p. 139 - 144, 2017.
- YIANATOS, J. Fluid flow and kinetic modelling in flotation related processes: columns and mechanically agitated cells - a review. Chemical Engineering Research and Design, v. 85, n. 12, p. 1591-1603, 2007.
- ZWIETERING, T. N. The degree of mixing in continuous systems. Chemical Engineering Science, v. 11, p. 1-15, 1959.
Publication Dates
-
Publication in this collection
13 Jan 2021 -
Date of issue
Jan-Mar 2021
History
-
Received
30 June 2019 -
Accepted
19 Sept 2020