Abstract
Real non-spherical particles can be modeled using the Discrete Element Method (DEM) with sphere clusters, superquadrics, or polyhedral particles. However, in applications involving a considerable number of particles, the analysis can become impracticable. The goal of this study is to demonstrate how well spherical particles can reproduce the flow of differently shaped particles. In this analysis, four dry particles are employed with different shapes and sphericity: spherical particles and three non-spherical particles, constituted by a combination of three spherical particles. For each non-spherical particle ensemble, the respective angles of repose were determined with DEM simulations using a simple virtual flow box experiment. Next, the flow of spherical particles through the flow box was calibrated to reach the same angle of repose for each non-spherical particle ensemble by tuning friction coefficients. A comparison of the computational time of the simulations for each non-spherical particle and their spherical representation is presented and discussed. The results show that using spherical particles in DEM simulations reduces the computational processing time in relation to the use of irregular forms in the simulations by approximately 80%.
Keywords:
DEM method; calibration; particle sphericity; particle shape
Keywords:
DEM method; calibration; particle sphericity; particle shape
1. Introduction
The Discrete Element Method (DEM) (Cundall and Strack, 1979CUNDALL, P. A.; STRACK, O. D. L. A discrete numerical model for granular assemblies. Géotechnique, v. 29, n.1, p. 47-65, 1979.) is a numerical method widely used for validation and optimization of particulate handling system designs. The great advantage of this methodology is the virtual visualization of the material flow.
In real situations, with bulk materials constituted by non-spherical particles, modeling the particles using spherical particles generally results in lower interparticle friction compared to real granular material friction (Coetzee, 2016COETZEE, C. Calibration of the discrete element method and the effect of particle shape. Powder Technology , v. 297, p. 50-70. 2016.). To solve this problem, two classes of methods are employed. The first class of methods is generating a non-spherical particle model using sphere clusters, superquadrics, or polyhedral particles (Irazábal et al., 2017IRAZÁBAL, J.; SALAZAR, F.; OÑATE, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Computers and Geotechnics, v. 85. p. 220-229, 2017.). Sphere clusters or clamps are formed by overlapping spheres to form a non-spherical particle (Shi et al, 2015SHI, C.; LI, D.; XU, W.; WANG, R. Discrete element cluster modeling of complex mesoscopic particles for use with the particle flow code method. Granular Matter, v. 17, n. 3, p. 377-387, 2015.). Superquadrics (Cleary, 2010CLEARY, P. DEM prediction of industrial and geophysical particle flows. Particuology, v. 8, n.2, p. 106-118, 2010. ) are a family of geometric shapes defined by various shape parameters in the mathematical formulation; therefore, ellipsoids and other quadric shapes can be obtained (Podlozhnyuk et al., 2017PODLOZHNYUK, A.; PIRKER, S.; KLOSS, C. Efficient implementation of superquadric particles in Discrete Element Method within an open-source framework. Computational Particle Mechanics, v. 4, n. 1, pp 101-118, 2017.). Polyhedral particle models enable the use of sharp corners and edges (Irazábal et al., 2017IRAZÁBAL, J.; SALAZAR, F.; OÑATE, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Computers and Geotechnics, v. 85. p. 220-229, 2017.). Applications of polyhedral particles can be found in Mack et al. (2011)MACK, S.; LANGSTON, P.; WEBB, C.; YORK, T. Experimental validation of polyhedral discrete element model. Powder Technology , v. 214, n. 3, p. 431-442, 2011., Govender et al. (2014)GOVENDER, N.; WILKE, D.; KOK, S.; ELS, R. Development of a convex polyhedral discrete element simulation framework for NVIDIA Kepler based GPUs. Journal of Computational and Applied Mathematics, v. 270, p. 386-400, 2014. and Höhner et al. (2014)HÖHNER, D.; WIRTZ, S.; SCHERER, V. A study on the influence of particle shape and shape approximation on particle mechanics in a rotating drum using the discrete element method. Powder Technology , v. 253, p. 256-265, 2014.. However, all ofthe approaches in the first class of methods have the disadvantage of a high computational cost, i.e., the computational time required to process the contacts between thousands of non-spherical particles can make the analysis impracticable.
In the second class of methods, the real particles are modeled as spherical particles, but an additional torque is included in the model, the rolling resistance torque. Therefore, the rolling friction is used as an effort to model the effect of the irregular shape of real particles. There are different formulations for modeling rolling resistance. Ai et al. (2011)AI, J.; CHEN, J.; ROTTER, J.; OOI, J. Assessment of rolling resistance models in discrete element simulations. Powder Technology, v. 206, n. 3, p. 269-282, 2011. and Irazábal et al. (2017)IRAZÁBAL, J.; SALAZAR, F.; OÑATE, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Computers and Geotechnics, v. 85. p. 220-229, 2017. discussed four types of rolling resistance models. The simplicity and lower computational requirements of this class of methods makes them preferable to implement in DEM commercial packages.
Barrios et al. (2013)BARRIOS, G. K. P.; CARVALHO, R. M.; KWADE, A.; TAVARES, L. M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technology , v. 48, p. 84-93, 2013. developed a methodology to measure the real particle parameters, as sliding friction, rolling angle, and coefficient of restitution, based on individual particle measurements, and employed a technique of an overlapping spheres model to reproduce the real shape of iron ore pellet particles. These authors performed an interesting study comparing slump test experiment results with DEM simulation, using both spherical modeling and the overlapping spheres model. They showed that simulations considering the overlapping spheres model produces better results than the spheres model. However, the authors used in their simulation the same the rolling friction parameter encountered in the procedure to achieve the relationship between the experimental rolling angle and the coefficient of rolling friction for the DEM simulations. If the rolling friction was issued from the calibration process, in a tuning process, the results with the sphere particle model could be better. Similar as performed by Li et al. (2017)LI, C.; HONEYANDS, T.; O'DEA, D.; MORENO-ATANASIO, R. The angle of repose and size segregation of iron ore granules: DEM analysis and experimental investigation. Powder Technology , v. 320, p. 257-272, 2017., also using iron ore pellets, this concept is the basis for the methodology that will be shown in this present article.
In a study on the mixing uniformity of irregular sand and gravel materials in a rotating drum, Jiang et al. (2019) combined the methodologies presented by Barrios et al. (2019)BARRIOS, G. K. P.; CARVALHO, R. M.; KWADE, A.; TAVARES, L. M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technology , v. 48, p. 84-93, 2013. and Li et al. (2017)LI, T.; PENG, Y.; ZHU, Z.; ZOU, S.; YIN, Z. Discrete element method simulations of the inter-particle contact parameters for the mono-sized iron ore particles. Materials, v. 10, n. 5, p.1-14, 2017. . They used the individual parameter measurement from the Barrios methodology and the tuning process for the rolling friction coefficient definition similar to the Li study. They modelled the gravel particle using the overlapping spheres technique and the sand was modelled as spherical particles. The DEM simulation results using V-box and the L-box agreed well with the experimental data. Wei et al. (2019)WEI, H.; TANG, X.; GE, Y.; LI, M.; SAXÉNB, H.; YU, Y. Numerical and experimental studies of the effect of iron ore particle shape on repose angle and porosity of a heap. Powder Technology , v. 353, p. 526-534, 2019. also utilize slump test experiments to determine the coefficient of rolling friction for iron ore pellets, employing spherical particles for the DEM simulation. They also perform experiments with cylindrical and conical particles prepared in the laboratory with magnetite powder. For the DEM simulation corresponding to these experiments, the author also used overlapping spheres. All experiments were well represented by the DEM simulations, where the static and rolling friction coefficients was differently set by a specific calibration procedure.
The main motivation of the present article is the need to calibrate the flow of iron ore or manganese ore fines, as they are commonly exported by the Brazilian mining companies. These products present greatly irregular shapes with a strong presence of adhesion and cohesion forces. Figure 1 presents a series of pictures performed by the authors using a Veho 800xmicroscope, showing the iron ore particle fines (sinter feed) in different moisture contents. Observe the greater non-uniform shapes of the particles, also the large influence of Van der Waals attraction forces, where the ultrafine particles adhere to the larger particles, and the cohesion forces effect originated by the capillary cohesion.
Iron ore sinter feed at different moisture contents: (a) 0%, (b) 3.7%, (c) 6.7%, (d) 8.5%, (e) 10.1%, (f) 12.1%.
Based on this fact, the methodology employed by the authors to simulated these ore fines is to use only spherical virtual DEM particles, with an adequate calibration process. In order to separate the particle shape effect from the adhesion and cohesion effects, this article presents and demonstrates the capability of DEM simulation of real non-spherical particle flow, using virtual spherical particles, in a case with minor influence of adhesion and cohesion forces. Of course, for a granular media with more uniform irregular particle shape, as wood chips(as in Xia et al., 2019XIA, Y.; LAI, Z.; WESTOVER, T.; KLINGER, J.; HUANG, H.; CHEN, Q. Discrete element modeling of deformable pinewood chips in cyclic loading test. Powder Technology , v. 345, n. 1, p. 1-14, 2019.) or agricultural particles (as in Ma et al., 2015MA, Z.; LI, Y.; XU, L. Discrete-element method simulation of agricultural particles motion invariable-amplitude screen box. Computers and Electronics in Agriculture, v. 118, p. 92-99, 2015.), for example, it is suitable to use a virtual particle with a similar geometry to that of the real particles. Also in some cases in the mining industry, as in the ROM crushing, this particle modeling is suitable.
In this context, the present article presents a study on the modeling of irregular shaped particles, such as spherical particles, using the Hert-Mindlin (no-slip) with RVD (Relative Velocity Dependent) Rolling Friction as the contact force model implemented in EDEM 2.4 (DEM Solutions, 2015). Therefore, this article aims to demonstrate how well spherical particles can reproduce the flow of different shaped particles and the computational processing time saved using this procedure.
Initially, a spherical particle is modeled based on Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002.. This is the reference particle. Next, a non-spherical particle is modeled by overlapping the reference particle. A group of these non-spherical particles is simulated in a flow box forming a sand pile with a specific angle of repose, and the simulation processing time is computed. To achieve the same angle of repose for the non-spherical particle sand pile, the parameters (including rolling friction) of the spherical reference model were calibrated, and when the flow simulation resulted in the same angle of repose, the processing time was computed and compared with the previous case. This process was repeated for two other non-spherical particles of different sphericity values.
The remainder of this article is organized as follows: Section 2 describes the mathematical model used in the DEM simulations, the spherical reference model, and calculation of the sandpile angles of repose. Section 3 presents the non-spherical particles used in analyses and the simulation procedures. Section 4 presents and discusses the numerical results. Finally, the study’s conclusions are given in Section 5.
2. DEM modeling and simulations
2.1 Mathematical model
The DEM method considers the discrete nature of granular material, treating the forces and moments on each particle individually. The forces involved in the dynamics of the contacts are modeled and included in Newton's second law, resulting in a system of coupled ordinary differential equations for translational and rotational motion (Eqs. 1 and 2) that are solved by numerical integration.
where mi and Ii are, respectively, the mass and moment of inertia of particle i; Vi and ω i are, respectively, the translational and rotational velocity of particle i; Fn, ij, F dn, ij, Ft, ij, F dt, ij are the contact forces (normal and damping forces); T i, j and τ i, j are the torques on particle i from particle j as a result of the total contact force (the sum of the normal and tangential forces) and rolling friction, respectively; F nC i, K is the non-contact force acting on particle i by particle k or other sources; F fi is the particle-fluid interaction force on particle i; and mi g is the gravitational force (Zhou et al., 2002ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002.; Zhu et al., 2007ZHU, H. P.; ZHOU, Z. Y.; YANG, R. Y.; YU, A. B. Discrete particle simulation of particulate systems: theoretical developments. Chemical Engineering Science , v. 62, n. 13, p. 3378-3396, 2007.).
In computational codes, the equations of motion are implemented using different contact force models that can be chosen according to the specific application. In this study, the DEM simulations were performed using the EDEM2.4 computational code (DEM Solutions, 2014) and the Hert-Mindlin (no-slip) with RVD (relative velocity dependent) rolling friction model. This model uses the traditional Hert-Mindlin model (Di Renzo and Di Maio 2004DI RENZO, A.; DI MAIO, F. Comparison of contact force models for the simulation of collisions in DEM based granular flow codes. Chemical Engineering Science, v. 59, n.3, p. 525- 541, 2004.) with a rolling friction model based on Zhou et al. (1999)ZHOU, Y. C.; WRIGHT, B. D.; YANG, R. Y.; XU, B. H.; YU, A. B. Rolling friction in the dynamic simulation of sandpile formation. Physica A: Statistical Mechanics and its Applications, v. 269, n. 2, p. 536-553, 1999.. This RVD rolling friction torque model is a generalization of the A-type model discussed in Ai et al. (2001)AI, J.; CHEN, J.; ROTTER, J.; OOI, J. Assessment of rolling resistance models in discrete element simulations. Powder Technology, v. 206, n. 3, p. 269-282, 2011. . The torque depends on the relative rotational velocity of two particles in contact, particle i and particle j, as follows:
where µ r is the coefficient of rolling friction, Fn is the contact normal force, ωrel is the unit vector of relative rotational velocity of the two particles in contact, and R is the equivalent radius of two particles in contact:
According to Ai et al. (2011)AI, J.; CHEN, J.; ROTTER, J.; OOI, J. Assessment of rolling resistance models in discrete element simulations. Powder Technology, v. 206, n. 3, p. 269-282, 2011. , there should be caution when using the A-type rolling friction model in static situations. In this model, there is a high residual kinetic energy due to rapid oscillation of the rolling friction torque. The high residual kinetic energy can be reduced by using an appropriate time step; the time between each computational interaction. A stable and trustworthy simulation is obtained when the time step is less than a critical time step (usually between 20%and 40%). In EDEM, the critical time step is the Rayleigh time step (Marigo and Stitt, 2015MARIGO, M.; STITT, E. H. Discrete element method (dem) for industrial applications: Comments on calibration and validation for the modelling of cylindrical pellets. KONA Powder and Particle Journal, v. 32, p. 236-252., 2015.; Li et al., 2017LI, T.; PENG, Y.; ZHU, Z.; ZOU, S.; YIN, Z. Discrete element method simulations of the inter-particle contact parameters for the mono-sized iron ore particles. Materials, v. 10, n. 5, p.1-14, 2017. ), given by:
where rp is the particle radius, ρp is the particle density, G is the shear modulus and vp is Poisson’s ratio.
2.2 Spherical particle reference model
Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002. presented a study that calibrated a DEM simulation using a simple experiment with a compartmentalized rectangular box (henceforth referred to as flow box). The calibration process was obtained by tuning friction coefficients. This experiment is used as a reference for the current study. Herein, the average repose angle was obtained from flow simulations in a flow box with a middle plate and outlets at its ends (Fig. 2). In these simulations, initially, before discharging, the particles accumulated in the superior part of the box; next, the outlets were opened and two sandpiles formed. The repose angle (β) is given by Eq. (6), where the left side of box βL is obtained using measurements from the front (βlf) and back (verse) (βlv) of the box (Fig. 3). The same procedure for the right side is used to determine βR. The sandpiling process was repeated four times to generate an average angle of repose (β).
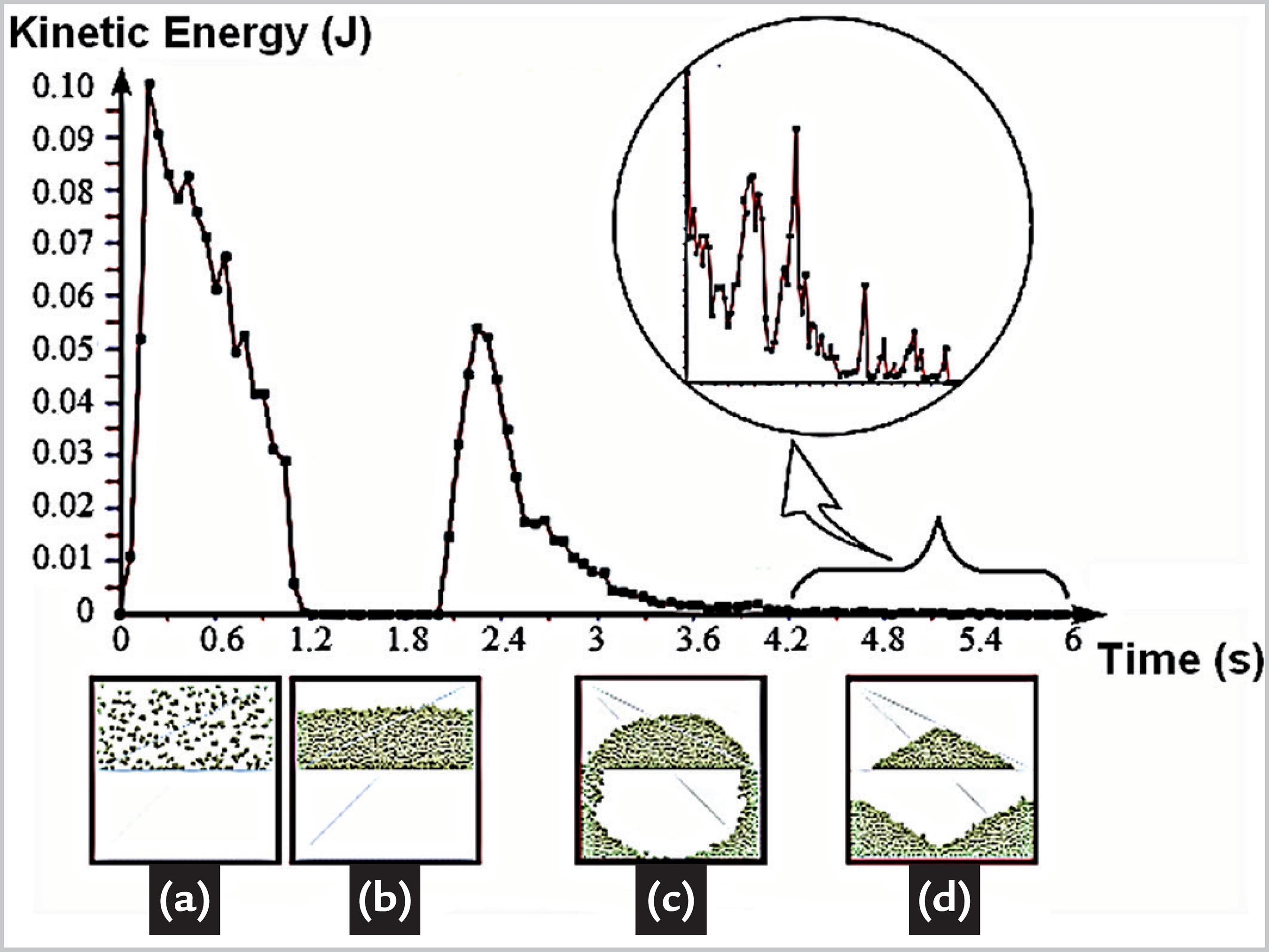
In the simulations, one task was to define the total computational time for a given simulation of a sand piling process. Therefore, the quantification of the kinetic energy of the entire system was used to decide when the simulation should be completed. The kinetic energy was computed during the process, and when the value reached residual values, after the sandpile formed at the bottom of the flow box (second rest - Fig. 3d), the simulation was completed, as shown in Fig. 3. This simulation time varies according to the particle shape.
In the simulations, initially, a spherical particle of glass with a diameter of 10 mm was defined as the reference. The particle model was defined based on Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002. modeling, according to Table1. The parameters of the calibrated spherical particle model from Zhou are shown in Table1.
Physical properties of the material (Zhou et al., 2002ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002.).
In the present study, the angle of repose from the DEM simulation is measured by editing the pictures from the final stage of flow through the flow box. The uncertainty of this procedure was estimated to be +/- 1.3%. Additionally, through a sensitivity analysis of the random deviation of this flow, there was computed a total uncertainty value for the numerical angle of repose of +/- 5.2%.
Using the same DEM parameters shown in Table1, the angle of repose was 28.9°, compared to the value of approximately 28.1° from Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002.. This result validates the DEM model developed for flow through a simple flow box, and is taken as a reference for evaluating the use of spherical particles to simulate the flow of non-spherical particles.
3. Non-spherical particle models and simulation procedure
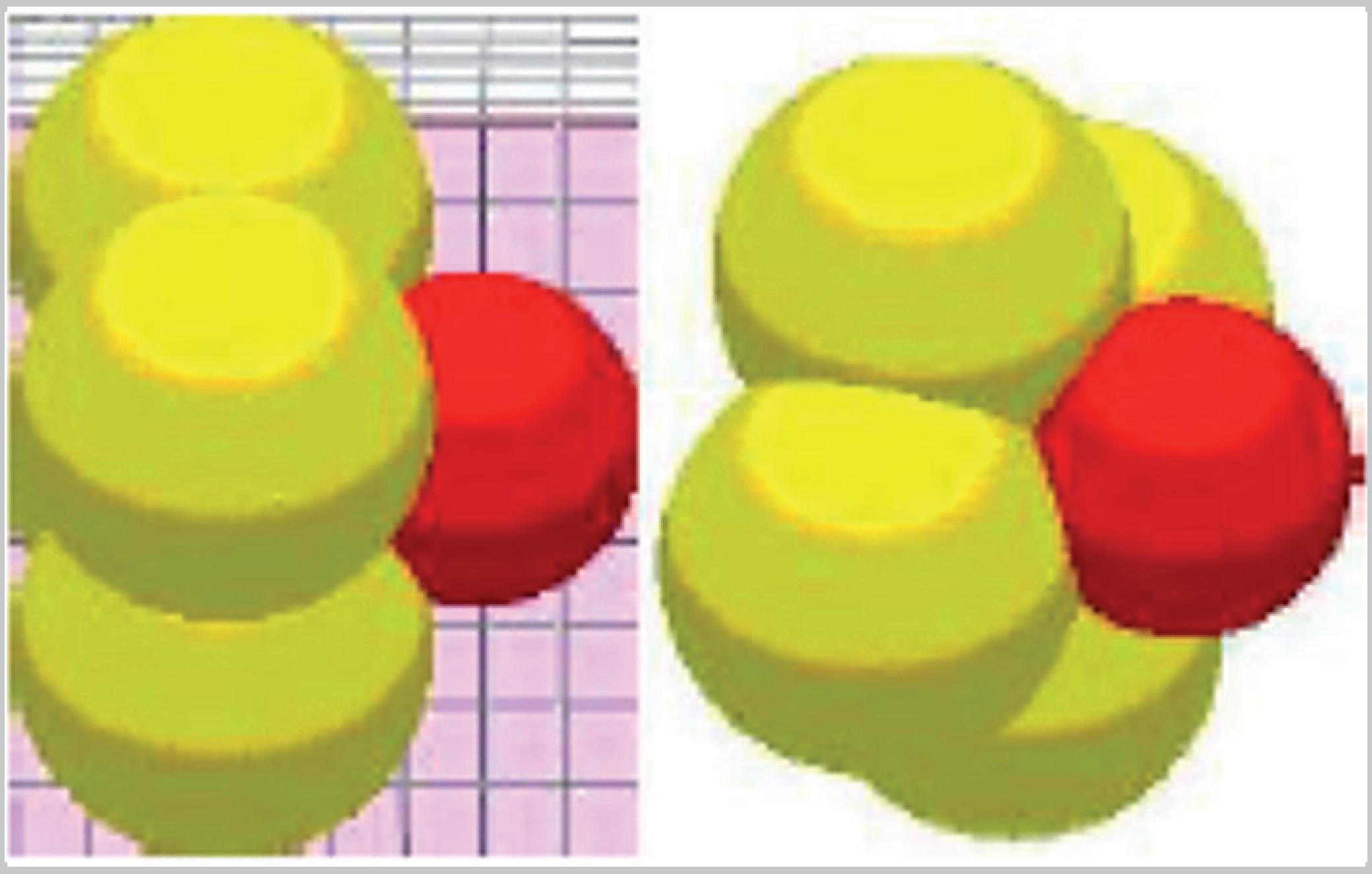
To analyze the flow of non-spherical particles, three shapes of particles were constructed by overlapping spheres in the EDEM. The three particles generated are inscribed in a 10-mm-diameter section (same diameter as the reference particle - Shape 1), as shown in Fig. 4. Shape 4 is shown at different views in Fig. 5.The criteria adopted to build the particle clusters was to maintain the new irregular particle circumscribed in the sphere of the 10mm diameter, in order to be similar to the Zhou et al. experiments with different sphericity values.
Total kinetic energy of the particles as a function of time. (a) particle generation; (b) rest; (c) flow; (d) rest.
Sphericity is the quantification of how closely a non-spherical shape approaches a perfect sphere. Mathematically, it is the ratio between the surface of a sphere whose volume is equivalent to that of the particle, Se, and the surface of the particle, Sp, i.e.
ψ = Se / Sp
The volume and surfaces of the four shapes were determine using SolidWorks. Therefore, the sphericity of the shapes could be determined (Table 2).
The simulation procedure can be divided into two parts. In the first part, four groups of materials were created. Each group formed with one particle shape is shown in Fig. 5. Each group was set to flow in the flow box, and at the end of the flow process, the angle of repose of the sandpile formed was measured (when the kinetic energy reached the lowest residual value) and the processing time was computed.
In the second part, the spherical particle (reference particle or Shape 1) was calibrated such that the angle of repose was the same as the sandpile of particles of Shape 2. The same procedure was repeated so the spherical particle had the same angle of repose as the sandpile of particles of Shape 3 and Shape 4. At the end of each simulation process of the reference particle, the computation time was computed and compared to the processing time of the non-spherical particle simulations in the first part of the simulation procedure.
4. Numerical results
4.1 Simulations in flow box
In the first part of the simulation, four groups of different particle shapes flowed through the flow box. Figure 7 shows the four groups of particles in the initial resting state at the top of the flow box. Each group has a different number of particles concentrated in a box volume with a height of 120 mm according to Fig. 7. After the initial rest, the particles flow through the box until the final rest (see comments in Section 2.3). Figure 8 shows the initial, intermediate, and final stages of the particle flow for Shape 2.
Initial stages of the simulation: (a) Shape 1, with 2000 particles; (b) Shape 2, with 5200 particles; (c) Shape 3, with 4200 particles; (4) Shape 4, with 4000 particles.
4.2. Mean angle of repose of the particles
The angles of repose of the sandpiles for the four groups of particles in the first part of simulations are shown in Table 2. The angle of repose differed for each shape, demonstrating the influence of non-spherical shapes. Table 3 also presents the computation time for each simulation. The spherical shape has the lowest computation time and smallest angle of repose.
4.3. Calibration of spherical model to reproduce non-spherical particles
The next step (Part 2 of the simulation procedure) was to recalibrate the parameters of the spherical model to reproduce the flow of non-spherical particles in order to reach the same angle of repose. The parameters (of the spherical model) were changed to obtain the angle of repose for particles of Shape 2, Shape 3 and Shape 4 shown in Table 4. This calibration process was performed according to Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002. by varying parameters to reach the desired angle of repose.
Variables considered for calibration of reference particle to represent non-spherical shapes.
Comparing Table 1 and Table 4, the main parameter changed was the rolling friction coefficient. The sliding friction coefficient µs,pw, restitution coefficient epw, particle specific mass ρ, shear modulus G, and Poisson's coefficient, remained unchanged during the calibration process.
Table 5 shows a comparison of the angle of repose of non-spherical particles and spherical particles calibrated to have approximately the same angle of repose. The computational processing time for this procedure is presented in Fig. 9.
According to Table 4, the use of spherical particles can represent the behavior of dry non-spherical particles in simulations using DEM in the formation of sandpiles, i.e., sandpiles with the same angle of repose can be obtained.
The use of spherical particles in the simulations brings a great computational gain. In the results, the flow simulation of the Shape 2 particle in the flow box had a computational processing time of 57.78 minutes. With the use of spherical particles in the representation of the Shape 2 particle, the computational processing time was reduced by 79.65%, i.e., the processing time was 11.76 minutes. For Shape 3, the reduction was 85.29%, and for Shape 4, the reduction was 82.05%.
On the dynamics of the flow, a question that could be posed is the time for the particles to settle in resting position as function of their shape. In the present methodology, this aspect can be analyzed following the technique used for the establishment of final time of the simulation, as represented on Figure 3. In the numerical tests, it was observed that the increase of the rolling friction also increases the time required for the final state of the simulation. For all cases tested, the simulations were included in the time interval of 6 seconds of the granular flow. However, this is important to note that if the dynamics has an important role in a particular case, this must be analyzed in detail. In the objective of the authors, chute flow, this aspect is not relevant for the steady regimes
The use of this methodology can be extended to the simulation of wet granular flow including adhesion and cohesion coefficients in the necessary additional contact force. The most common method used for this purpose is the JKR model, based in the classical model proposed by Johnson et al. (1971)JOHNSON, K. L.; KENDALL, K.; ROBERTS, A. D. Surface energy and the contact of elastic solids. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, v. 324, n. 1558, p. 301-313, 1971., which was largely employed for the DEM simulation of cohesive granular flow, as discussed by Umer and Siraj (2018)UMER, M.; SIRAJ, M. S. DEM studies of polydisperse wet granular flows. Powder Technology , v. 328, p. 309-317, 2018. The authors of this present article have employed the presented methodology to study some iron fines or chute flow (Nogueira et al, 2012NOGUEIRA, L. R.; PATROCÍNIO, M.; MARINHO, C., MACIAS, P. H. S., ROCHA, D. M., AMARANTE MESQUITA, A. L. Transfer chute and belt conveyor performance using the Discrete Element Method for Coasting analysis. In: INTERNATIONAL CONGRESS OF THE SCIENCE AND TECHNOLOGY OF IRONMAKING, 6th., Rio de Janeiro, RJ, Brazil. Proceeding […]. Rio de Janeiro: ICSTI, 2012.; Carvalho et al., 2014CARVALHO, L. C. S.; SANTOS, E. G.; AMARANTE MESQUITA, A. L., MESQUITA, A. L. A.; GOMES, L. M. Analysis of capillary cohesion models for granular flow simulation: application for iron ore handling. In: BRAZILIAN CONGRESS OF THERMAL SCIENCES AND ENGINEERING, 15th., 2014, Belém, Pará, Brazil. Proceedings […]. Belém: ENCIT, 2014.), hydrate alumina chute flow (Mascarenhas et al., 2013MASCARENHAS, F. P.; MESQUITA, A. L. A.; AMARANTE MESQUITA, A. L. Simulation of transfer chute operation using the discrete element method. In: IBERO-LATIN AMERICAN CONGRESS ON COMPUTATIONAL METHODS IN ENGINEERING, 34th., 2013, Pirenópilis, Goiás, Brazil. Proceeding […]. Pirenópolis: CILAMCE, 2013. ) and manganese chute flow (Mesquita et al, 2018MESQUITA, H.; MACIAS, P. H. S.; AMARANTE MESQUITA, A. L.; PINHEIRO, K. A.; MESQUITA, A. L. A.; SOUZA, H. S.; OLIVEIRA, A. H.; BRITO, H. L. S. Aplicação do método dos elementos discretos para modelagem e simulação do escoamento de minério de manganês. Revista Engenharia e Tecnologia, v. 10, n. 2, p. 41-50, 2018.).However, concerning the use of this methodology, in some cases, it is necessary to use irregulated particle shapes, for example, the flow of elongated particles in the ROM crushing process.
5. Concluding remarks
This article presented a methodology of representing dry non-spherical particles with spherical particles using DEM. The motivation for this procedure is the reduction of computational time. The methodology consisted of calibrating the spherical particle model parameters to reach the same angle of repose of the non-spherical particles. The sliding and rolling friction parameters from the particle-particle interaction were verified to be the most prominent in the calibration procedure, with the last parameter having the largest influence.
The numerical study was carried out using the experiment presented by Zhou et al. (2002)ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002. as a reference for calibration. After validation of the DEM model for the case of spherical particles, the flow of three different assemblies of non-spherical particles were simulated using spherical particles, following the calibration procedure previously defined.
The results showed that the use of spherical particles in DEM simulations reduced the computational processing time in relation to the use of irregular forms in the simulations by approximately 80%. Enormous savings were obtained, showing the advantage this strategy offers.
Finally, it is worth mentioning that this study does not permit generalizations for other applications, such as elongated particles in the ROM crushing process, or where the aspect ratio has an important role in the granular flow. Also, it is important to note that if some aspect relative to the dynamic of the granular flow is relevant, as example, the time it takes for the particle to arrive at complete repose. For different cases, specific studies should be conducted, which is a great challenge for designers and engineers. However, it is possible to anticipate the great advantage in reduction of the computational time with reliable results, and also that the methodology can be extended to the wet granular flow, considering all the questions discussed in the article.
Acknowledgments
The authors would like to express their gratitude for the financial support from Vale Company, ITV (Vale Institute of Technology), and PROPESP/UFPA (Call PAPQ 01/2018).
References
- AI, J.; CHEN, J.; ROTTER, J.; OOI, J. Assessment of rolling resistance models in discrete element simulations. Powder Technology, v. 206, n. 3, p. 269-282, 2011.
- BARRIOS, G. K. P.; CARVALHO, R. M.; KWADE, A.; TAVARES, L. M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technology , v. 48, p. 84-93, 2013.
- CARVALHO, L. C. S.; SANTOS, E. G.; AMARANTE MESQUITA, A. L., MESQUITA, A. L. A.; GOMES, L. M. Analysis of capillary cohesion models for granular flow simulation: application for iron ore handling. In: BRAZILIAN CONGRESS OF THERMAL SCIENCES AND ENGINEERING, 15th., 2014, Belém, Pará, Brazil. Proceedings […] Belém: ENCIT, 2014.
- CLEARY, P. DEM prediction of industrial and geophysical particle flows. Particuology, v. 8, n.2, p. 106-118, 2010.
- COETZEE, C. Calibration of the discrete element method and the effect of particle shape. Powder Technology , v. 297, p. 50-70. 2016.
- CUNDALL, P. A.; STRACK, O. D. L. A discrete numerical model for granular assemblies. Géotechnique, v. 29, n.1, p. 47-65, 1979.
- HERTZ-MINDLIN (no slip) with RDV Rolling Friction model. In: EDEM 2.6 Theory Reference Guide. Edinburgh, Scotland: DEM Solutions, 2014.
- DI RENZO, A.; DI MAIO, F. Comparison of contact force models for the simulation of collisions in DEM based granular flow codes. Chemical Engineering Science, v. 59, n.3, p. 525- 541, 2004.
- GOVENDER, N.; WILKE, D.; KOK, S.; ELS, R. Development of a convex polyhedral discrete element simulation framework for NVIDIA Kepler based GPUs. Journal of Computational and Applied Mathematics, v. 270, p. 386-400, 2014.
- HÖHNER, D.; WIRTZ, S.; SCHERER, V. A study on the influence of particle shape and shape approximation on particle mechanics in a rotating drum using the discrete element method. Powder Technology , v. 253, p. 256-265, 2014.
- IRAZÁBAL, J.; SALAZAR, F.; OÑATE, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Computers and Geotechnics, v. 85. p. 220-229, 2017.
- JOHNSON, K. L.; KENDALL, K.; ROBERTS, A. D. Surface energy and the contact of elastic solids. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, v. 324, n. 1558, p. 301-313, 1971.
- LI, C.; HONEYANDS, T.; O'DEA, D.; MORENO-ATANASIO, R. The angle of repose and size segregation of iron ore granules: DEM analysis and experimental investigation. Powder Technology , v. 320, p. 257-272, 2017.
- LI, T.; PENG, Y.; ZHU, Z.; ZOU, S.; YIN, Z. Discrete element method simulations of the inter-particle contact parameters for the mono-sized iron ore particles. Materials, v. 10, n. 5, p.1-14, 2017.
- MA, Z.; LI, Y.; XU, L. Discrete-element method simulation of agricultural particles motion invariable-amplitude screen box. Computers and Electronics in Agriculture, v. 118, p. 92-99, 2015.
- MACK, S.; LANGSTON, P.; WEBB, C.; YORK, T. Experimental validation of polyhedral discrete element model. Powder Technology , v. 214, n. 3, p. 431-442, 2011.
- MARIGO, M.; STITT, E. H. Discrete element method (dem) for industrial applications: Comments on calibration and validation for the modelling of cylindrical pellets. KONA Powder and Particle Journal, v. 32, p. 236-252., 2015.
- MASCARENHAS, F. P.; MESQUITA, A. L. A.; AMARANTE MESQUITA, A. L. Simulation of transfer chute operation using the discrete element method. In: IBERO-LATIN AMERICAN CONGRESS ON COMPUTATIONAL METHODS IN ENGINEERING, 34th., 2013, Pirenópilis, Goiás, Brazil. Proceeding […] Pirenópolis: CILAMCE, 2013.
- MESQUITA, H.; MACIAS, P. H. S.; AMARANTE MESQUITA, A. L.; PINHEIRO, K. A.; MESQUITA, A. L. A.; SOUZA, H. S.; OLIVEIRA, A. H.; BRITO, H. L. S. Aplicação do método dos elementos discretos para modelagem e simulação do escoamento de minério de manganês. Revista Engenharia e Tecnologia, v. 10, n. 2, p. 41-50, 2018.
- NOGUEIRA, L. R.; PATROCÍNIO, M.; MARINHO, C., MACIAS, P. H. S., ROCHA, D. M., AMARANTE MESQUITA, A. L. Transfer chute and belt conveyor performance using the Discrete Element Method for Coasting analysis. In: INTERNATIONAL CONGRESS OF THE SCIENCE AND TECHNOLOGY OF IRONMAKING, 6th., Rio de Janeiro, RJ, Brazil. Proceeding […] Rio de Janeiro: ICSTI, 2012.
- PODLOZHNYUK, A.; PIRKER, S.; KLOSS, C. Efficient implementation of superquadric particles in Discrete Element Method within an open-source framework. Computational Particle Mechanics, v. 4, n. 1, pp 101-118, 2017.
- SHI, C.; LI, D.; XU, W.; WANG, R. Discrete element cluster modeling of complex mesoscopic particles for use with the particle flow code method. Granular Matter, v. 17, n. 3, p. 377-387, 2015.
- UMER, M.; SIRAJ, M. S. DEM studies of polydisperse wet granular flows. Powder Technology , v. 328, p. 309-317, 2018
- XIA, Y.; LAI, Z.; WESTOVER, T.; KLINGER, J.; HUANG, H.; CHEN, Q. Discrete element modeling of deformable pinewood chips in cyclic loading test. Powder Technology , v. 345, n. 1, p. 1-14, 2019.
- WEI, H.; TANG, X.; GE, Y.; LI, M.; SAXÉNB, H.; YU, Y. Numerical and experimental studies of the effect of iron ore particle shape on repose angle and porosity of a heap. Powder Technology , v. 353, p. 526-534, 2019.
- ZHOU, Y. C.; XU, B. H.; YU, A. B.; ZULLI, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technology , v. 125, n.1, p. 45-54, 2002.
- ZHOU, Y. C.; WRIGHT, B. D.; YANG, R. Y.; XU, B. H.; YU, A. B. Rolling friction in the dynamic simulation of sandpile formation. Physica A: Statistical Mechanics and its Applications, v. 269, n. 2, p. 536-553, 1999.
- ZHU, H. P.; ZHOU, Z. Y.; YANG, R. Y.; YU, A. B. Discrete particle simulation of particulate systems: theoretical developments. Chemical Engineering Science , v. 62, n. 13, p. 3378-3396, 2007.
Publication Dates
-
Publication in this collection
22 June 2020 -
Date of issue
Jul-Sep 2020
History
-
Received
29 July 2019 -
Accepted
17 Feb 2020