Abstract
This article analyzes the effectiveness of hedging Brazilian soy oil, soy meal, and soybeans in the Chicago Board of Trade (CBOT) and in the Brazilian Commodities and Futures Exchange (BM&F) to reduce the risk of financial loss due to commodity price fluctuations. The econometric results show that a cross-hedging strategy using the BM&F soybean futures contract is an instrument of low effectiveness for managing soy oil and soy meal price risk. Despite low effectiveness, the estimates demonstrate total advantage for soy meal hedging operations using CBOT soy meal futures contracts rather than cross-hedging using BM&F soybean futures contracts. With some exceptions, the results are also more favorable for hedging soy oil with soy oil futures contracts at the CBOT rather than cross hedging with soybeans at the BM&F. Conversely, Brazilian traders hedging soybeans receive more effective risk protection by trading soybean futures contracts at the BM&F than by trading soybean futures contracts at the CBOT.
cross-hedging; soybean industry; hedging effectiveness
Hedging with futures contracts in the brazilian soybean complex: BM&F vs. CBOT
Andréia Regina O. da SilvaI; Danilo R. D. AguiarII; João Eustáquio de LimaIII
I Economist, M.S. in agricultural economics by Federal University of Viçosa.
II Associate professor of agricultural economics at Federal University of Viçosa, 36.571-000, Viçosa, MG, Brazil. E-mail: danilo@ufv.br
III Professor of agricultural economics at Federal University of Viçosa, 36.571-000, Viçosa, MG, Brazil. E-mail: jelima@ufv.br
ABSTRACT
This article analyzes the effectiveness of hedging Brazilian soy oil, soy meal, and soybeans in the Chicago Board of Trade (CBOT) and in the Brazilian Commodities and Futures Exchange (BM&F) to reduce the risk of financial loss due to commodity price fluctuations. The econometric results show that a cross-hedging strategy using the BM&F soybean futures contract is an instrument of low effectiveness for managing soy oil and soy meal price risk. Despite low effectiveness, the estimates demonstrate total advantage for soy meal hedging operations using CBOT soy meal futures contracts rather than cross-hedging using BM&F soybean futures contracts. With some exceptions, the results are also more favorable for hedging soy oil with soy oil futures contracts at the CBOT rather than cross hedging with soybeans at the BM&F. Conversely, Brazilian traders hedging soybeans receive more effective risk protection by trading soybean futures contracts at the BM&F than by trading soybean futures contracts at the CBOT.
Key words: cross-hedging, soybean industry, hedging effectiveness.
1. Introduction
Agricultural futures contracts have become important tools for the management of price risk. By means of the purchase or sale of these contracts while holding opposite positions in the physical market, farmers, agribusiness managers, grain elevators operators, and international traders are protected against adverse price variation. This strategy, known as hedging, is based on the correlation between the price negotiated for a commoditys futures contract and the cash price of the same commodity. If the current and future prices are correlated, the financial loss in one market (future or current) tends to be, at least partially, compensated for by the earnings obtained from holding the opposite position in the other market.
The soybean complex is among the sectors of the Brazilian economy that demand careful administration to control financial risk. Several facts illustrate the importance of this sector in the Brazilian economy. Brazil is now the world second largest producer of soybeans and the largest exporter of soybean meal. Brazilian exports of the complexs principal products (beans, oil, and meal) reached more than US $4 billion in 2000, which corresponds to about 8% of the countrys total export value. In 2001, the value of the soy product exports increased to US$ 5.297 billion (ABIOVE).
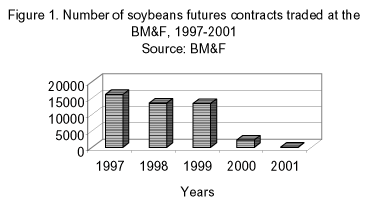
In spite of the expressive performance reflected in the numbers shown above, traders who operate with soybeans and soybean products are still in need of the same risk management tools that are available to their main competitors, the North Americans. In the United States, specific futures contracts are available for each of the soybean complexs products at the CBOT, while the Brazilian exchange only offers soybean futures contracts. To make this situation even worse, trade of soybean futures contracts at the BM&F, which was already quite small in relation to the number of contracts negotiated at the Chicago Board of Trade (CBOT), drastically diminished after 1999 (Figure 1) and was interrupted in 2001. Due to this situation, evidenced in Figure 1, the BM&F reformulated its soybeans futures contract operations in 2002 to attract more investors and generate the liquidity necessary for market operations.
An issue that arises in this setting is whether the BM&F soybean futures market meets the liquidity requirements and offers the products needed to reduce risk. In other words, does the BM&F soybean futures market allow risk reductions similar to the risk reductions that Brazilian hedgers would obtain using CBOT soy futures contracts? The answer to this question not only reflects the past value of BM&F futures contracts, but also gives an indication of the reformulated contracts potential effectiveness as a hedging tool.
Although hedges are normally made with futures contracts for the same commodity being traded in the spot market, specific futures contracts for a given commodity are not always obtainable. The unavailability of futures contracts for all commodities leads to the use of futures contracts underpinned by commodities merely related to the one for which risk protection is intended: cross-hedging. Only soybean futures contracts are available in the BM&F. The soybean complexs multi-dimensional product mix makes hedging in the Brazilian market more difficult, as cross-hedging is often the only available hedging option.
Using BM&F futures contracts, traders can hedge current soybean positions with soybean futures contracts; however, traders wishing to hedge current positions in soy oil or meal must cross hedge with soybean futures contracts. These same traders can directly hedge any of their current soy product positions using the soybean, meal, and oil futures contracts available in international exchanges, such as the CBOT. As the three soy products prices can move in different directions and intensities, the effectiveness of a soy product cross-hedging strategy is reduced. Therefore, the viability of any soy product cross-hedging strategy should be evaluated empirically case by case.
The objective of this paper is to compare alternative hedging strategies for traders of soybeans, soy oil, and soy meal from the main Brazilian producer regions. The alternative strategies are defined by the use of either BM&F or CBOT soy product futures contracts as the hedge. The period of analysis runs from 1998 to 2000, just before the drastic reduction in Brazilian contract trading. A comparative analysis between the soybean contracts traded at the BM&F and CBOT has already been conducted by Lazzarini (1997). The authors study employed statistical tests to measure the effectiveness of the direct hedge in the two exchanges and verified an advantage gained through use of the Brazilian exchange. Our work differs from Lazzarinis (1997) in the period and regions considered and in the inclusion of soy oil and meal in the analysis. In addition, our paper uses more current econometric methodology.
The paper is organized in three sections besides this introduction. The next section, section 2, presents the portfolio theory that was applied to the futures markets and empiric procedures employed. Section 3 reports and discusses the empirical results, and section 4, the final section, offers our conclusions.
2. Methodology
2.1. Theoretical model
Assuming that the hedger is a risk averse investor with a portfolio composed by two assets: one in the cash market and one in the futures market. Admit that the hedgers objective is to minimize of risk as expressed by negative revenue variation. As Blank et al. (1991) and Stoll and Whaley (1993) show, the revenue of a hedging trader is given by:
R h = V(p2-p1)-F(f2-f1)
(1)
Where,
R h is the revenue in a portfolio with positions in both futures and cash markets;
V is the size of the position in the cash market;
(p2-p1) is the price difference in the cash market from period 1 to period 2;
F is the size of the position in the futures market; and
(f2-f1) is the price difference in the futures market between periods 1 and 2.
Solving expression (1) for V, one obtains
R h / V= (p2-p1)-h(f2-f1)
(2)
where h is the hedge ratio (F/V).
By applying the property of the variance of a sum to equation (2), the variance of the revenue by unit of product is obtained:
s h2 = s p2 2h s p f + h2s f2
(3)
where,
s h2 is the variance of the revenue for unit of product;
s p2 is the variance of the price change in the cash market;
s p f is the covariance between price changes in the cash market and in the futures market; and
s f 2 is the variance of the change of the futures price.
From the first order condition for minimizing revenue variance, the optimum hedge ratio (h *) is obtained by deriving the revenue variance with regard to h:
¶ s h2 / ¶ h= -2s p f + 2h s f 2 =0 ,
s p f = h s f 2 ,
h* = s p f / s f 2
(4)
Therefore, the optimum hedge ratio, h*, depends on the covariance between the change in futures price and cash price and on the variance of the futures price.
The same model allows the calculation of hedging effectiveness, which is the proportion of revenue variance that can be eliminated through the adoption of a portfolio with the optimum hedge ratio. Mathematically, hedging effectiveness can be represented as:
where Var(h *) is the variance in the revenue from a portfolio with the optimum hedge ratio, and Var(p) is the variance of revenue from a portfolio without a hedge.
Var(p) is the same as the variance of the change of the cash price s 2p, since the variance of revenue without hedging depends only on the behavior of the cash price. Var(h*) can be obtained by substituting (4) in (3):
Simplifying:
Recalling that the linear correlation (r) between two variables is the ratio between their covariance and the product of their respective standard deviations [r pf=(s pf/s fs p)], one can multiply and divide the last element of the equation above for s 2p to obtain a formula involving the correlation:
Substituting s 2p and (6) into (5) one gets
Equation (7) shows that when the optimum hedge ratio is used, the hedges effectiveness is the square of the correlation between the changes in cash and futures prices. The hedges effectiveness varies from zero to one (0 £ e £ 1), reaching its highest level when the changes in cash and futures prices are perfectly correlated and decreasing as the price correlation diminishes. Consequently, the more related the product traded in the cash market is to the product traded in the futures market, the greater the correlation between both markets prices tends to be and the higher the hedging effectiveness.
2.2. Analytical model
2.2.1. Calculus of the optimum hedge ratio
Considering that the coefficient of the inclination of a simple regression done by least ordinary square is the same as the covariance between the dependent and the independent variables divided by the variance of the independent variable, and that the determination coefficient (R2) is the same as the square of the coefficient of linear correlation, many authors have estimated the optimum hedge ratio and hedging effectiveness using regressions between the future price and the cash price, either by level, by differences, or by relative differences1 1 See, for instance, Ederington (1979), Carter and Lyons (1985), and Brown (1985). .
However, Myers and Thompson (1989) demonstrate that the equations conventionally used, whether by level (pt = a o + a 1ft + e t), by differences (D pt = a o + a 1D f t + e t), or by relative differences (D pt/pt-1 = a o + a 1D ft/ft-1 + e t), are not appropriate for estimating the optimum hedge ratio except under special conditions. These authors argue that in the theoretical model, the covariance and variance are conditioned by the information available at the moment of decision-making; however, in simple regression models, the inclination coefficient just generates a ratio of unconditional covariance and variance of the explanatory variable.
To remove such limitation, Myers and Thompson (1989) developed a generalized model in which estimation of the optimum hedge ratio takes into account the available information at the moment of decision. This model is given by:
pt = a o + a 1ft + a(L)pt-1 + b(L)ft-1 + e t
(8)
where pt is the cash price in period t; pt-1 is the cash price with one lag; ft is the futures price in period t; ft-1 is the futures price in the previous period; L is the lag operator; a(L) and b(L) are polynomials in L with parameters to be estimated; a o and a 1 are parameters to be estimated; and e t is a random error. Like other regression models, the estimate of the optimum hedge ratio consists of the coefficient a 1.
This generalized model allows the inclusion of other information that impacts the cash price, therefore, permitting variables such as production, stock, exports, and consumer income to be included in equation (8). It is noted that if tests of unitary root show that the series are integrated of first order, equation (8) should be specified using the first differences, in other words, D pt and D ft should be used in place of pt and ft.
2.2.2. Calculus of hedging effectiveness
After optimum hedge ratio is estimated, the hedges effectiveness is calculated. Since the estimated regression presents explanatory variables other than average futures price, the coefficient of determination no longer reproduces the value of hedging effectiveness. The following procedure is adopted to calculate hedging effectiveness: after estimating the optimum hedge ratio using Myers and Thompsons model, A) the series of returns from both hedged and unhedged positions are calculated; B) the variances between these series are calculated; and C) effectiveness is calculated by substituting the variance estimates directly into equation (5).
2.2.3. Data and procedures2 2 The econometric procedures were carried out by means of the software EVIEWS version 03.
This research uses secondary daily time series data covering the period from August 05, 1998, to September 15, 2000. The series begins in 1998 because the series of cash prices was first generated in 1998. FNP Consultoria e Pesquisas database provided the exchange rate series and the daily wholesale prices of soybeans (R$ per 60kg bag), soy meal (R$/ton), and soy oil (R$ per ton) in the Brazilian states of Bahia (Barreiras), Paraná (Cascavel, Campo Mourão, Maringá and Ponta Grossa), Mato Grosso (Cuiabá and Rondonópolis), Rio Grande do Sul (Passo Fundo), Santa Catarina (Chapecó), Minas Gerais (Uberlândia), Goiás (Rio Verde), Mato Grosso do Sul (Dourados) and São Paulo (Orlândia). Since these 13 regions were chosen to achieve results for Brazil as a whole, they include regions that are not among the countrys most important soy producing regions. Soybean futures prices in Brazil (in US$/60kg bag) were obtained from the BM&F; futures prices of oil (US cents/lb), meal (US$/ton) and soybeans (cents/bushel) at the CBOT were obtained from the database of Consultoria, Métodos, Assessoria e Mercantil LTDA- CMA. All the price series were converted to US$/ton.
The futures price series were constructed using the date of contract expiration (the first delivery date) at the CBOT as the base date. As contract expiration at the CBOT occurs on the 15th day of each delivery month, that day was used as the base date at both the CBOT and the BM&F. After the date of contract expiration was rationalized between the two markets, weekly series (112 observations) and biweekly series (56 observations) were organized using every Wednesdays data. Wednesday was chosen because it is the most active trading day in both exchanges. If Wednesday was a holiday, the preceding Tuesday or following Thursday was substituted.
After the series were built, unit root tests were carried out to verify if they were stationary. This test is justified because one of the presuppositions of the regression analysis, and of most conventional estimation methods, is that the series are stationary, in other words, their stochastic properties are time invariant (Pindyck and Rubinfeld, 1991).
Using the following equation, the augmented Dickey-Fuller test is applied to test stationarity of each series:
D yt = m + g D yt-1+ d 1D yt-1 + d 2D yt-2 + ... + d p-1D yt-p+1 + e t
(9)
The hypothesis that g =0 and the alternative hypothesis that g <0 are then tested. If the equations calculated value is larger than the critical values tabulated by Dickey and Fuller (1979), the hypothesis of unitary root exists is rejected and the series is considered stationary [integrated of order zero, I(0)]. If the hypothesis of unitary root is not rejected, the series is non-stationary or integrated of an order superior to zero. In this case, the Dickey-Fuller test is redone to determine if the series of differences are integrated of first order [I(1)], and so forth.
After the application of the unit root test, the regressions were estimated. The lag operator used in the generalized equation was a polynomial in L, defined in the regressions through the AKAIKE criterion. This criterion was defined for each one of the estimated regressions, through which operators were tested in polynomial form and chosen using the smaller value criterion.
3. Results and Discussion
Results from the augmented Dickey-Fuller tests do not reject the unit root hypotheses for any of the regional prices and futures prices series. It was observed that all the series presented unitary root at 1% significance, becoming stationary in the first differences3 3 The results of the unit root tests were omitted to save space. ; consequently, the regressions were estimated with the variables in first differences.
3.1. Weekly series results
3.1.1. BM&F
Table 1 gives the results from analysis of the weekly series of soy product hedges at the BM&F over the studied period for each region (recall that only soybean futures contracts are traded in the BM&F). The relatively low effectiveness levels and high optimum hedge ratios make cross-hedging soy meal or soy oil with BM&F soybean futures contracts of little attraction.
The table shows that the effectiveness of cross-hedging a position in soy oil with BM&F soybean futures contracts varies by region from 3.7% to 30.17% (Table 1, col.7). These low optimum effectiveness values indicate that this cross-hedging operation is an unappealing risk protection option. At the highest effectiveness level, the case of the trader operating with soy oil from Maringá, cross-hedging soy oil using BM&F soybean futures contracts at the at the optimum calculated hedge ratio of 2.08 (a trader wanting protection for 1,000 t of soy oil held in the physical market is optimally cross hedged by selling soybean futures contracts totaling 2,080 t in the BM&F) would remove only 30.17% of his risk of financial loss due to negative price fluctuations. The relatively high optimum hedge ratio further reduces this hedging strategys appeal, as the number of futures contracts that must be traded to reach this ratio greatly increases costs. In general, similar behavior was found in all analyzed regions: high optimum hedge ratios and low hedging effectiveness make cross hedging soy oil in the BM&F an uninteresting risk management strategy.
Soy meal traders looking for risk protection through use of BM&F soybean futures contracts would also be disappointed. This hedging strategy had a degree of regional effectiveness that varied from a very unhelpful negative 12.66% to an only slightly better 14.58%4 4 Of course, negative effectiveness estimates do not make sense. They would suggest that a hedge increases risk. In general, negative estimates occurred in the models that had the worst econometric adjustments. . As with soy oil, the correlation between soybean price and soy meal prices was not great enough to make cross-hedging at the BM&F advantageous.
For soybean traders, the effectiveness of hedging at the BM&F varies from 44.61% to 84.38%, depending on region, on average quite superior to the estimates for oil and meal cross-hedging. Focusing on the highest and lowest effectiveness values for the hedging soybeans with BM&F soybean futures contracts, a trader located in Cascavel with a position in the physical market of 1000 60 kg bags of soybeans would have to negotiate the equivalent of 765 bags (.765 optimum ratio) in the futures market to gain a risk reduction as large as 84%, while a trader located in Orlândia, holding the same position of 1000 bags in the physical market would have to negotiate 408 bags in the futures market to obtain a risk reduction of (just) about 45%. In general, this hedging strategy permitted risk reduction above 60% in all regions except Campo Mourão and Orlândia. It is interesting to note that the least effective hedge was found to be in Orlândia, which is in the state where the BM&F is located.
The results from the BM&F weekly prices series suggest that the design of this exchanges soybean futures contract matched most of Brazils regional soybean markets and is an appropriate instrument for use by soybean traders in the Brazilian market to reduce price risk. The same cannot be said about cross-hedging either soy meal or oil holdings with BM&F soybean futures contracts; these risk reduction strategies were shown to be unviable.
3.1.2 CBOT
Analysis of the results of hedging Brazilian soybean positions with CBOT soybean futures contracts (Table 2) shows that this strategy is less effective than hedging the same product using BM&F soybean futures contracts. Ponta Grossa was the only region with CBOT hedging effectiveness superior to 50%, which does not compare well with the 83.57% effectiveness of the same hedge using BM&F futures contracts. This result leads to the assumption that the BM&F soybean futures contract reflects the Brazilian domestic soybean markets characteristics better than the CBOT contract. Notice that even the low volume of trade in the BM&F contract was not sufficient to impede a high price correlation between the Brazilian soybean cash and futures markets.
It was found that the direct hedge of Brazilian soy meal with CBOT soy meal futures contracts was more effective than the cross hedge of meal with BM&F soybean futures contracts. However, even using the CBOTs contract, risk reduction is insignificant, with a hedging effectiveness of slightly above 50% in only two studied regions: Maringá and Ponta Grossa, both in the state of Paraná.
Hedging soy oil using the CBOTs soy oil futures contract was only minimally more effective than cross-hedging soy oil with the BM&Fs soybean futures contract, and both strategies are unsatisfactory. The effectiveness of oil cross-hedging at the BM&F was inferior to 30% while effectiveness using the CBOT contract didn't surpass 40% Interestingly, it was found that the CBOT hedge had an advantage over the BM&F cross hedge in only four of the thirteen analyzed regions, Barreiras, Cascavel, Orlândia, and Passo Fundo; and six of the optimum hedge ratio estimates for the CBOT oil contract were not significant, even at 10%, as compared to just one for the BM&F contract. These results need careful analysis.
3.2 Biweekly series results
3.2.1 BM&F
Table 3 gives the effectiveness and optimum ratio estimates made using series of biweekly BM&F data. The estimated parameters for the optimum soybean hedge ratio at the BM&F were significant at 1% for all the analyzed regions. The estimated optimum soybean futures to soybeans hedge ratio oscillated between 0.5727 and 0.9800, while hedging effectiveness oscillated between 48.57% and 88.34%. The areas of Cascavel, Chapecó, Cuiabá, Maringá, Passo Fundo, Ponta Grossa, Rondonópolis and Uberlândia presented average soybean hedging effectiveness of 84.37%, while Campo Mourão and Orlândia showed the lowest levels of risk reduction, 48.57% and 51.45% respectively
For soy meal traders, an examination of the biweekly series shows that cross hedge operations using the BM&F soybean contract were totally unviable. At the best, risk reduction was just 15.97% at the optimum hedge ratio, and 92.30 of the examined regions did not present significant values for this ratio.
The bi-weekly series showed that traders of Brazilian soy oil would be able to reduce their level of risk only slightly through use of the BM&F soybean futures contract cross hedge. The values for this hedges effectiveness oscillated between 14.83% and 35.76% while the regional average optimum hedge ratio was an extremely high 2.04
3.2.2 CBOT
Results from the bi-weekly series of CBOT hedges are given in Table 4. The table shows that use of the optimal ratio of CBOT soybean futures contracts to reduce Brazilian soybean price risk was somewhat effective, although less effective than the use of BM&F soybean futures contracts. In the biweekly series soybean hedging efficiency using the CBOT contract ranged from 57.87% in Ponta Grossa to 17.89% in Orlândia
For soy meal traders, with few exceptions, use of CBOT soy meal futures contract to hedge their risk was more interesting than cross-hedging with BM&F soybean futures contracts (Table 3). Using the optimum ratio of CBOT soy meal futures contracts to soy meal, the regions of Maringá, Orlândia and Ponta Grossa show relatively high hedge effectiveness levels of 62.31%, 53.99% and 61.65% respectively. The region of Cuiabá presented the smallest level of effectiveness for this hedge, 19.15%, with a very low optimum hedge ratio, .1418.
Despite the insignificant CBOT soy oil hedging efficiency estimates for Dourados, Ponta Grossa, Rondonópolis, and Uberlândia and the miniscule estimate for Chapecó (7.9%), some regions traders could benefit by using this hedge. The state of São Paulo, represented by Orlândia, presented a reasonably advantageous 63.18% level of price risk reduction though use of the CBOT oil futures contract at the optimum ratio of .7229. A trader that had a position of 1000 tons of soy oil in the Orlândia cash market would need to negotiate the equivalent of 723 tons of soy oil futures contracts at the CBOT to reduce his risk of negative revenue variation due to price change by 63.18%.
3.3. Results Summary
The estimates made using biweekly data were very similar to the ones generated using weekly observations except in the case of the soy oil hedge. This general similarity brings more consistency to the following summary of the results. In the case of soybeans, the relationship between cash and futures prices favored the domestic exchange. The effectiveness of the soybean hedge with the BM&F soybean futures contract was about 36% superior to the effectiveness of a hedge with the CBOT soybean contract.
Soy meal hedging using the CBOT meal futures contract was consistently found to be a more effective risk reduction strategy than cross hedging soy meal with soybeans at the BM&F. The series of soy meal hedges with CBOT meal futures contracts shows that meal traders in the studied regions gained at best an average risk reduction of 42% with a small optimum ratio and minimal interregional variation.
There was divergence between the biweekly and the weekly soy oil hedging results. The biweekly series shows that, in 77% of the regions, soy oil hedging at the CBOT reduces risk more effectively than cross hedging at the BM&F, however, the weekly series shows just the opposite to be true: the BM&F soy oil cross hedge offers more effective risk protection in 70% of the regions. This apparent contradiction suggests that one need be careful when broadly assuming that one hedging strategy offers better risk protection than another in that market. In addition, it should be noted that the optimum ratios needed to effect the most efficient BM&F soy oil hedging strategies are extremely high in almost all regions in both series, which makes this strategys cost effectiveness a concern.
The CBOT soy oil futures hedge for Orlândia oil traders was the most effective CBOT hedge (63% risk reduction in the biweekly series) and more effective than any BM&F cross hedge, but at the best, oil traders in the studied regions gained an average risk reduction of only 37% at the CBOT with extreme interregional variation (Table 4). What can be taken from the soy oil hedging analysis is that both hedging and cross hedging in the soy oil market do not reduce price risk substantially.
The following three generalizations are therefore made:
The BM&Fs soybean futures contract is more effective than the CBOTs for hedging soybean positions in the studied regions. Average soybean risk protection provided by the BM&F contract reached its peak of 76% in the biweekly series. The CBOT soybean contracts average protection peaked at 40% in the same series. Futures prices in the BM&F stayed strongly correlated with the cash prices in most of Brazils soybean producing regions.
Brazilian soy meal hedging using the CBOT soy meal futures contract was found to be clearly more effective than cross-hedging using the BM&F soybean futures contract, but the effectiveness of the hedge using the CBOT contract is still quite low. The effectiveness of the CBOT hedge rose above 60% in only two regions: Maringá, and Ponta Grossa in the state of Paraná.
Hedging Brazilian soy oil with either of the strategies analyzed in this research was not a particularly effective method of managing the risk of soy oil price fluctuation. Soy oil hedging at the CBOT did prove to be a more effective risk reduction strategy than cross hedging at the BM&F, at least in biweekly series, but the possible benefits from hedging soy oil at the CBOT are small, except possibly for those trading soy oil in Orlândia.
4. Conclusions
This paper shows that the soybean futures contract traded at the BM&F can be of great usefulness to farmers, cooperatives, agro-industries, exporters and other agents in the Brazilian soy market for the management of their price risk, in spite of the low volume of trade in this contract over recent years. Soybean hedging in the BM&F futures market was found to be a more attractive option than soybean hedging at the CBOT, offering average price risk protection across all regions of 76% in the biweekly series. It was also determined that Brazilian soy oil and soy meal cross hedges with BM&F soybean futures contracts had very little effect on price risk; moreover, except in a very few of the studied regions, hedging Brazilian oil or meal with oil or meal futures contracts at the CBOT also had little effect.
Although it is known that high trade volume contributes to a greater correlation between cash and futures prices, which is essential for hedging operations to be effective, the results reported in this analysis suggest that the correlation between the cash and futures prices of Brazilian soybeans was greater in the BM&F than in the CBOT. In other words, the similarity-effect, which is the effect of similarity between the characteristics of the cash market and the contractual design of the futures market overcame the liquidity-effect, which tends make the greatest price correlation a result of the more efficient arbitrage available in larger liquidity markets. However, the results obtained by the soybeans hedgers in the BM&F would even be better if contract trade at the BM&F was more liquid.
Increased trading volume not only improves the correlation between cash and future prices but should also reduce transaction costs and facilitate the close of positions for traders who do not want delivery. These benefits may spill over into soybean product cross hedges, making that price risk protection strategy more attractive. In the final analysis, the studys results show that Brazilian soybean product traders would benefit from the growth of the Brazilian soybean futures market. Soybean traders certainly would as they get quite inferior protection in the Chicago commodities futures exchange
It is not so apparent that speculators operating in the Brazilian soybean market benefit from hedging at the Brazilian commodity futures exchange. This exchanges illiquidity puts off many speculators fearing that they will not be able to offset their positions when they want to leave the market. The drastic reduction in trade volume in the BM&Fs soybean futures market when contractual reformatting eliminated the cash settlement rule made this evident. The cash settlement rule provided speculators with security; although, it was undesirable from a traders viewpoint.
The key for the success of a futures contract is in its design, which must be attractive to both traders looking to protect their investment and speculators hoping to make a quick paper profit and get out of the market. If this balance is reached, the vicious cycle of low liquidity will be ended and all parties will win.
References
ABIOVE Associação Brasileira das Indústrias de Oils Vegetais. (http://www.abiove.com.br).
BM&F - BOLSA DE MERCADORIAS & FUTUROS.(http://www.BM&F.com.br).
BLANK,S.C.;CARTER,C.A; SCHMIESING,BH. Futures and options markets- trading in commodities and financials. Englewood cliffs: Prentice-Hall, Inc.;1991.410p.
BROWN,S.L. A reformulation of the portfolio model of hedging. American Journal Agricultural Economics. v67, 1985, p508-512.
CARTER,C.A., LYONS,R.M.A Hedging feedlot cattle: a Canadian perspective. American Journal Agricultural Economics, v. 67,1985. p.32-39.
Consultoria, Métodos, Assessoria e Mercantil LTDA- CMA. (http://www.CMA.com.br).
DICKEY,D.A,FULLER,W.A. Distribution of the estimator for auto-regressive time series with unit root. Journal of American Statistical Association,v74,1979.427-431p.
EDERINGTON,LM. The hedging performance of the new futures markets, The journal of Finance, v.34, 1979. p 157-170.
FNP- Consultoria e Comércio.(http://www.fnp.com.br).2001.
LAZZARINI, S.G. Gerenciamento de riscos de preços no sistema agroindustrial brasileiro da Soybeans. Revista de Economia e Sociologia Rural. Brasília: SOBER, vol. 35, nº 4, Out./Dez., 1997. p.41-64.
MYERS,R.J. e THOMPSON, S.R, Generalized optimal hedge ratio estimation American Agricultural Economics Association. Copyright nov/1989. 858-867p.
PINDYCK,R.S.,RUBINFELD,D.L. Econometric models e economic forecasts. New York: Mc Graw-Hill, 1991.497p
STOLL, H.R. e WHALEY,R.E, Hedging with futures contracts. Futures and Options-theory and applications. Cincinnati: South-Western Publishing Co., 1993. 413.p.
- ABIOVE Associação Brasileira das Indústrias de Oils Vegetais. (http://www.abiove.com.br).
- BLANK,S.C.;CARTER,C.A; SCHMIESING,BH. Futures and options markets- trading in commodities and financials Englewood cliffs: Prentice-Hall, Inc.;1991.410p.
- BROWN,S.L. A reformulation of the portfolio model of hedging. American Journal Agricultural Economics v67, 1985, p508-512.
- CARTER,C.A., LYONS,R.M.A Hedging feedlot cattle: a Canadian perspective. American Journal Agricultural Economics, v. 67,1985. p.32-39.
- Consultoria, Métodos, Assessoria e Mercantil LTDA- CMA. (http://www.CMA.com.br).
- DICKEY,D.A,FULLER,W.A. Distribution of the estimator for auto-regressive time series with unit root. Journal of American Statistical Association,v74,1979.427-431p.
- EDERINGTON,LM. The hedging performance of the new futures markets, The journal of Finance, v.34, 1979. p 157-170.
- FNP- Consultoria e Comércio.(http://www.fnp.com.br).2001.
- LAZZARINI, S.G. Gerenciamento de riscos de preços no sistema agroindustrial brasileiro da Soybeans. Revista de Economia e Sociologia Rural. Brasília: SOBER, vol. 35, nº 4, Out./Dez., 1997. p.41-64.
- MYERS,R.J. e THOMPSON, S.R, Generalized optimal hedge ratio estimation American Agricultural Economics Association. Copyright nov/1989. 858-867p.
- PINDYCK,R.S.,RUBINFELD,D.L. Econometric models e economic forecasts New York: Mc Graw-Hill, 1991.497p
- STOLL, H.R. e WHALEY,R.E, Hedging with futures contracts Futures and Options-theory and applications. Cincinnati: South-Western Publishing Co., 1993. 413.p.
Publication Dates
-
Publication in this collection
16 July 2003 -
Date of issue
June 2003