Inferring phenotypic causal structures among body weight traits via structural equation modeling in Kurdi sheep

ABSTRACT.

Data collected on 2550 Kurdi lambs originated from 1505 dams and 149 sires during 1991 to 2015 in Hossein Abad Kurdi Sheep Breeding Station, located in Shirvan city, North Khorasan province, North-eastern area of Iran, were used for inferring causal relationship among the body weights at birth (BW), at weaning (WW), at six-month age (6MW), at nine-month age (9MW) and yearling age (YW). The inductive causation (IC) algorithm was employed to search for causal structure among these traits. This algorithm was applied to the posterior distribution of the residual (co)variance matrix of a standard multivariate model (SMM). The causal structure detected by the IC algorithm coupling with biological prior knowledge provides a temporal recursive causal network among the studied traits. The studied traits were analyzed under three multivariate models including SMM, fully recursive multivariate model (FRM) and IC-based multivariate model (ICM) via a Bayesian approach by 100,000 iterations, thinning interval of 10 and the first 10,000 iterations as burn-in. The three considered multivariate models (SMM, FRM and ICM) were compared using deviance information criterion (DIC) and predictive ability measures including mean square of error (MSE) and Pearson's correlation coefficient between the observed and predicted values (r(y, ŷ)) of records. In general, structural equation based models (FRM and ICM) performed better than SMM in terms of lower DIC and MSE and also higher r(y, ŷ). Among the tested models ICM had the lowest (36678.551) and SMM had the highest (36744.107)DIC values. In each case of the traits studied, the lowest MSE and the highest r(y, ŷ) were obtained under ICM. The causal effects of BW on WW, WW on 6MW, 6MW on 9MW and 9MW on YW were statistically significant values of 1.478, 0.737, 0.776 and 0.929 kg, respectively (99% highest posterior density intervals did not include zero).

Keywords:
causal effects; growth traits; predictive ability; sheep

Introduction

In livestock species, body weight of domestic animals at different ages has deterministic effects on the profitability of breeding enterprises. Therefore, these traits may be considered as efficient selection criteria for developing breeding programs (Tosh & Kemp, 1994). Selection of the best animals for body weight recorded at different ages to be parents of the next generation is a possible way for increasing meat production (Boujenane & Kansari, 2002). Because of nutritional habits, mutton is the main source of animal protein in Iran and approximately 40 percent of red meat supplied through sheep production which does not satisfy the increasing demand of consumers. Therefore, increasing production efficiency in any sheep breeding system is required (Rashidi, Mokhtari, Jahanshahi, & Abadi, 2008). Developing an appropriate selective procedure considering breeding values requires accurate estimates of genetic parameters obtained under multivariate models.

Rosa et al. (2011) pointed out that in any breeding program dealing with multiple trait genetic evaluation; it is of great importance to study potential causal relationships among the traits. In the classical animal breeding and genetic evaluation programs, breeding values of the selection candidates are predicted under standard mixed models (SMMs), which ignore the potential causal relationships may exist among the traits (Valente, Rosa, Gianola, Wu, & Weigel, 2013). Gianola and Sorensen (2004) developed theory of quantitative genetics to become suitable for situations in which causal relationships including recursiveness or simultaneity exists between the phenotypes in a multivariate system. Structural equation models (SEMs) enable fitting and studying cause-and-effect relationships between phenotypes (Wright, 1934) and were first introduced in genetics by Wright (1921) but have been ignored in quantitative genetics for many years. The work of Gianola and Sorensen (2004) stimulated application of SEMs in animal breeding and genetics (Maturana et al., 2010; Valente, Rosa, Campos, Gianola, & Silva, 2010; Inoue et al., 2016; Mokhtari, Moghbeli Damaneh, & Arpanahi, 2018). Genetic parameters pertaining to SEMs can be useful for modeling biological relationships among phenotypes (Valente et al., 2010)

The application of structural equation models allows for inferring of direct genetic effects and the magnitude of causal effects between traits. A breeding strategy based only on standard multivariate model (SMM) would cause a delay in achieving the breeding goal if interventions, which would block indirect genetic effects, exist among the traits (Valente et al., 2013).

A number of studies have applied mixed effects structural equation models in the animal breeding context (Maturana et al., 2010; Mokhtari et al., 2018). However, these studies assumed that causal structures were known a priori. More recently, some studies fitted structural equation models based on a data- driven causal structure search, namely applications to European quail (Valente, Rosa, Silva, Teixeira, & Torres, 2011) and to bovine milk fatty acids (Bouwman, Valente, Janss, Bovenhuis, & Rosa, 2014).

Kurdi sheep is an important native dual-purpose (meat and milk) sheep breed in Iran, numbering about 3.5 million heads and mainly distributed in North Khorasan province, North-eastern of the country (Saghi, Shahdadi, Borzalabad, & Mohammadi 2018). The breed is kept mainly for meat production by nomadic pastoralists under low quality pastures (Saghi & Shahdadi, 2017), is fat-tailed, light-brown to yellowish in color, relatively large-sized and suitable for fattening purposes.

Previous studies conducted on genetic evaluation of growth traits in Kurdi sheep (Shahdadi & Saghi, 2016; Saghi et al., 2018) without considering possible causal relationships among them. AmouPosht-e Masari et al. (2018) studied genetic parameters for growth traits in Lori Bakhtiari sheep using structural equation models and showed the superiority of models considering causal effects among the growth traits on standard models which ignore them. To our knowledge there are no other reports on genetic evaluation of growth traits in breeds of sheep considering possible causal relationships among them. Therefore, the objectives of the present research were to infer possible causal relationships among the growth traits of Kurdi sheep and possibility of estimating genetic parameters of body weight traits in Kurdi sheep breed under SMMs and SEMs and to compare these models in terms of predictive ability.

Material and methods

Breed characteristics and flock management

This breed is mainly well known for its disease resistance, tolerance to unfavorable climatic conditions and suitable feed efficiency as well as adaptability to mountainous pastures. Coat color of Kurdi lambs is dark brown and black at birth, but gradually changed to gray at adulthood time (Saghi et al., 2018). Average mature live weights for Kurdi ewes and rams were 55 kg and 95 kg, respectively.

Maiden ewes were mated to rams for first time at about 18 months of age. In general, each one ram was mated to 25 randomly selected ewes, in a separate paddock for about 45 days from early October until mid-November. Consequently, lambing was started from mid-February and continued to late March. Newborn lambs identified by an ear tag, birth date, sex, birth weight, birth type and pedigree information were individually recorded within 24 h of birth. Lambs were weaned an average age of 90 days. Rams and ewes were typically maintained in flock for 2-3 and 7 years, respectively.

Data and the studied traits

In the present study pedigree information and data on body weight traits including birth weight (BW), weaning weight (WW), six-month weight (6MW), nine-month weight (9MW) and yearling weight (YW) that collected from 1991 to 2015 in Hossein Abad Kurdi Sheep Breeding Station, located in Shirvan city, North Khorasan province, North-eastern area of Iran, were used. Animals with body weights outside of the range mean ±2.5×S.D. have been removed from the data set. The structure of the data set used is presented in Table 1.

Statistical analyses

Significance testing of fixed effects and least square analyses were carried out using the general linear model (GLM) procedure of the Statistical Analysis System (SAS, 2004). Common fixed effects included in the models for the studied traits were sex of lambs in two classes (male and female), dam age at lambing in six classes (2-7 years old), birth year in 24 classes (1991-2015) and birth type in two classes (single and twin). Interactions among fixed effects were also fitted. Age of lambs at weaning, six-month and nine-month body weight weighing (in days) was considered as a linear covariate for WW, 6MW, 9MW and YW, respectively. The interactions between considered fixed effects were not significant and therefore dropped out.

Table 1
Descriptive statistics for the studied traits.

Item	Traits (kg)a
	BW	WW	6MW	9MW	YW
Mean	4.44	24.28	33.39	35.76	42.99
S.D.	0.69	4.92	5.95	7.02	8.62
Min.	2.10	10.50	16.80	13.70	20.20
Max.	7.20	41.00	53.00	63.00	69.00
C.V. (%)	15.54	20.26	17.82	19.63	20.05
No. of records	2550	2550	2550	2550	2550
No. of sires	149	149	149	149	149
No. of dams	1505	1505	1505	1505	1505

• ^a
  BW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight.

A restricted maximum likelihood (REML) procedure under a derivative free algorithm, applying Wombat program of Meyer (2007), was used and six models including different combinations of direct additive effects and maternal ones, including maternal additive genetic and maternal permanent environmental, were tested. The considered models (in matrix notation) are as below:

Model 2$\mathrm{y}=\mathrm{}{\mathrm{X}}_{\mathrm{b}}+\mathrm{}{\mathrm{Z}}_1\mathrm{a}+\mathrm{}{\mathrm{Z}}_3\mathrm{p}\mathrm{e}+\mathrm{e}$

Model 3 Cov (a,m) = 0$\mathrm{y}=\mathrm{}{\mathrm{X}}_{\mathrm{b}}+\mathrm{}{\mathrm{Z}}_1\mathrm{a}+{\mathrm{Z}}_2\mathrm{m}+\mathrm{e}$

Model 4 Cov (a,m) = Aσ_am$\mathrm{y}=\mathrm{}{\mathrm{X}}_{\mathrm{b}}+\mathrm{}{\mathrm{Z}}_1\mathrm{a}+{\mathrm{Z}}_2\mathrm{m}+\mathrm{e}$

Model 5 Cov (a,m) = 0$\mathrm{y}=\mathrm{}{\mathrm{X}}_{\mathrm{b}}+{\mathrm{Z}}_1\mathrm{a}+{\mathrm{Z}}_2\mathrm{m}+{\mathrm{Z}}_3\mathrm{p}\mathrm{e}+\mathrm{e}$

Model 6 Cov (a,m) = Aσ_am$\mathrm{y}={\mathrm{X}}_{\mathrm{b}}+{\mathrm{Z}}_1\mathrm{a}+{\mathrm{Z}}_2\mathrm{m}+{\mathrm{Z}}_3\mathrm{p}\mathrm{e}+\mathrm{e}$

where, y is a vector of records for the studied traits; b, a, m, pe and e are vectors of fixed, direct genetic, maternal genetic, maternal permanent environmental and the residual effects, respectively. The matrices of X, Z_a, Z_m and Z_pe are design ones associating corresponding effects to vector of y. Also, A is the numerator relationship matrix and σ_am denotes covariance between additive and maternal effects.

The Akaike’s Information Criterion (AIC) was applied for the determination of the most appropriate model among tested models (Akaike, 1974):

${\mathrm{A}\mathrm{I}\mathrm{C}}_{\mathrm{i}}=-2\mathrm{l}\mathrm{o}\mathrm{g}{\mathrm{L}}_{\mathrm{i}}+2{\mathrm{P}}_{\mathrm{i}}\mathrm{}$

where log L_i is the maximized log likelihood and p_i is the number of parameters fitted for model i. In each case, the model with the lowest AIC is considered as the best model.

Statistical inference

After selection of the most suitable model for the studied traits Bayesian Markov Chain Monte Carlo (MCMC) implementation was carried out applying the GIBBS2F90 program of Misztal et al. (2018), which implements Gibbs sampling to evaluate the posterior density of the parameter estimates. The length of the chain and the burn-in period were examined by visual inspection of the trace plots of posterior samples of the parameters in several preliminary analyses. For each model, 100,000 iterations were run and posterior samples from each chain were thinned considering thinning intervals of 10 iterations after discarding the first 10,000 iterations as burn-in. Hence, 9,000 samples were considered for computing features of the posterior distribution. Posterior analyses for calculating posterior means and posterior standard deviations were carried out applying the POSTGIBBSF90 program of Misztal et al. (2018).

It was assumed that the direct additive and maternal additive genetic effects followed a multivariate normal distributions, a priori, with a null mean vector and a (co)variance matrix G⊗A, where G and A are the genetic (co)variance matrix and numerator relationship matrix among animals, respectively. Furthermore, it was assumed that the vector of residual effects followed a multivariate normal distribution with a null mean vector and (co)variance matrix R ⊗I_n, where I_n is an identity matrix and R is the residual (co)variance matrix; ⊗ shows the Kronecker product. Multivariate normal distribution was also assumed for maternal permanent environmental effects, so that their fully conditional distributions were also multivariate normal. The prior distribution of the genetic (G) and maternal permanent environmental (Pe) (co)variance matrices were assumed to be inverted Wishart distribution, so that their fully conditional posterior distributions were also inverted Wishart (Sorensen & Gianola, 2002). The SEM models are not identifiable at the likelihood level due to the presence of extra parameters including structural coefficients. For achieving identification, it was assumed that residual correlations in system were uncorrelated. In the other words in SEMs, R was assumed to be a diagonal matrix for the identification purposes.

The Inductive Causation (IC) algorithm and structural equation modeling

The Inductive Causation was used to the residual (co)variances resulted in SMM, which ignored causal relationships among the traits, analysis. Valente et al. (2010) pointed out that the residual (co)covariances were investigated information from the joint distribution of the phenotypic traits conditional on genetic effects, such that they adjust the confounding issues caused by genetic effects when the traits are genetically correlated. The IC algorithm performs a series of statistical decisions based on partial correlations between traits, more information on IC algorithm presented in literature (Pearl, 2000; Inoue et al., 2016). Searching causal structure among the studied growth traits of Kurdi sheep was carried out applying the program written in R (R Development Core Team, 2009) by Valente and Rosa (2013).

Maturana, Legarra, Varona, and Ugarte (2007) pointed out that the method described by Gianola and Sorensen (2004) for incorporating causal effects in quantitative genetics is not straightforward enough to perform in a general manner and showed that recursive models could be handled by fitting parent trait as a covariate for other trait(s) while genetic correlations between traits are considered in multivariate analyses. In this case, parent trait denotes trait which causally influences on other trait(s). Therefore, this methodology was applied in the present study. Detailed information and the theoretical background about the methodology used in the present study for fitting recursive models are given by Maturana et al. (2007).

In the present study, two types of models based on structural equation molding were considered. The first model was based on graph revealed by inductive causation (IC) algorithm (Pearl, 2000). The IC algorithm allows searching for how variables are causally related. Applying simulated data, Valente et al. (2010) adapted the IC algorithm to a mixed models context and showed that applying this method to the posterior distribution of the residual (co)variance matrix of a standard multiple trait model (MTM) recovered the expected network. The IC-based model (ICM) is shown in Figure 1.

Figure 1
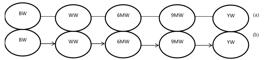
Undirected graph detected among the studied growth traits in Kurdi sheep by the IC algorithm with 90%, 95% and 99% of highest posterior density intervals (a). Directed causal structure by considering biological prior knowledge about relationship among the traits (b).

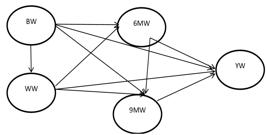
The second model was fully recursive model (FRM) in which assumed that any time temporal former traits causally influenced on all other traits after wards. In which, causal effects were assumed from BW on WW, 6MW, 9MW and YW, from WW on 6MW, 9MW and YW, from 6MW on 9MW and YW and finally from 9MW on YW (Figure 2).

The SMM, FRM and ICM were compared using deviance information criterion (DIC), the DIC takes the trade-off between model goodness-of-fit and corresponding complexity of model into account (Bouwman et al., 2014). Model with smaller DIC values are better supported by the data.

Figure 2
Fully recursive model considered among the studied body weight traits in Kurdi sheep.

Model comparisons

For assessing predictive ability of the tested models (SMM, FRM and ICM), the dataset was randomly partitioned five times into two sets including training set (50% of data set) and testing set (retained 50% data set). Then, solutions for all fixed and random effects of the training set were estimated and used to predict observations in the testing set. Predictive ability of the models was assessed by PREDICTF90 program of Mizstal et al. (2002) and compared applying two measures; first measure was mean square error (MSE) as follow:

$\mathrm{M}\mathrm{S}\mathrm{E}=\mathrm{}\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{({\mathrm{y}}_{\mathrm{i}}-\mathrm{}{\widehat{\mathrm{y}}}_{\mathrm{i}})}^2}{\mathrm{n}}$

where, y_i and ŷ_i denote i^th observed and predicted record for each trait in testing data set and n is the number of records in testing data set. Second measure was the Pearson correlation between observed and predicted values (r(y,ŷ)) in the testing set. The MSE and r(y,ŷ) values calculated five times and were averaged finally. The lower MSE and higher r(y,ŷ) value the higher superiority of the model superiority.

System parameters

The interpretation of parameters obtained under SEMs, the so-called system parameters in SEMs literature, is different from that of the analogous ones obtained under SMMs (Gianola & Sorensen, 2004). Therefore, further transformation is required to be able to compare (co)dispersion of random effects among two models fitted. Transformations for the estimated (co)variance matrices to the standard multivariate model scale were carried out as:

${\mathrm{G}}^{\mathrm{*}}=\mathrm{}{\mathrm{\Lambda }}^{-1}\mathrm{G}{\mathrm{\Lambda }}^{\mathrm{\text{'}}-1}$

${\mathrm{P}\mathrm{e}}^{\mathrm{*}}=\mathrm{}{\mathrm{\Lambda }}^{-1}\mathrm{P}\mathrm{e}{\mathrm{\Lambda }}^{\mathrm{\text{'}}-1}\mathrm{}$

${\mathrm{R}}^{\mathrm{*}}=\mathrm{}{\mathrm{\Lambda }}^{-1}\mathrm{R}{\mathrm{\Lambda }}^{\mathrm{\text{'}}-1}\mathrm{}$

and${\mathrm{}\mathrm{P}}^{\mathrm{*}}=\mathrm{}{\mathrm{\Lambda }}^{-1}\mathrm{P}{\mathrm{\Lambda }}^{\mathrm{\text{'}}-1}\mathrm{}$.

The matrices G*, Pe*, R* and P* have (co)variance components for direct additive and maternal additive genetic effects, maternal permanent environmental, residual and phenotypic effects, respectively, which first obtained under SEMs and then were transformed to their equivalents under SMMs. R* is a matrixwith non-zero off-diagonal elements. The matrix of structural coefficients (Λ) is a square one; off-diagonal elements were determined according to causal structures between the considered traits (Valente et al., 2010).

Results and discussion

The importance of maternal effects on the studied traits

The AIC values under the considered animal models are given in Table 2. Direct additive genetic and maternal additive genetic effects, without considering covariance between them, and maternal permanent environmental effects (Model 5) were random sources of variation for BW. While for WW only direct additive and maternal genetic effects, without considering covariance between them, (Model 3) were influencing random effects. Model 2, in which direct additive genetic effects and maternal permanent environmental effects were significant random effects, determined as the best one for 6MW and 9MW traits. Maternal effects had no influencing effects on YW. The maternal effects did not disappeared until 9 months of age, due to a carry-over effect after weaning. The importance of considering the maternal effects for genetic evaluation of the body weights of several sheep breeds have been well documented in the literature (Abegaz, Van Wyk, & Olivier, 2005; Rashidi et al., 2008).

Table 2
AIC values from univariate analysis for the studied traits with the best model in bold face.

Model	Traits a
	BW	WW	6MW	9MW	YW
Model 1	-27.588	8695.094	9537.932	10026.25	11132.97
Model 2	-82.63	8696.358	9534.112	10009.4	11134.92
Model 3	-49.076	8691.916	9538.138	10014.78	11134.97
Model 4	-55.718	8697.084	9538.23	10012.85	11136.46
Model 5	-85.754	8698.362	9536.114	10011.4	11136.92
Model 6	-79.59	8692.72	9535.616	10011.8	11138.29

• ^aBW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight. The best model is shown in bold face.

The Inductive Causation algorithm

Applying different (90, 95 and 99%) HPD intervals for the IC algorithm resulted in an undirected graph on causal structure among the studied growth curve traits in Kurdi sheep (Figure 1a). Considering biological prior knowledge on the temporal relationship among the traits over undirected graph (Figure 1a) revealed by IC algorithm resulted in a directed causal structure (Figure 1b). The latest graph is called IC-based model (ICM) throughout the manuscript. IC-algorithm revealed a time-temporal causal structure in such a way that each body weight trait only influence causally on body weight trait measured just next it but not on all other subsequent traits. In other words, each trait directly influences on trait just measured after it and indirectly influences on all other next traits.

Valente et al. (2011) applied the IC algorithm for searching phenotypic causal structures among some productive and reproductive traits of European quail and concluded that coupling prior knowledge with the output provided by the IC algorithm allowed further learning regarding phenotypic causal structures among the studied traits. Bouwman et al. (2014) explored causal structures involving bovine milk fatty acids applying the IC algorithm and concluded that the causal structure can provide more insight into underlying mechanisms involved among the traits and the structural equation model can predict conditional changes arising from such interventions. Inoue et al. (2016) inferred phenotypic causal networks among meat quality traits in Japanese Black cattle applying the IC algorithm coupling with biological prior knowledge. They concluded that by fitting a structural equation model, considering the causal structure based on the output of the IC algorithm, inferences about direct genetic effects and the magnitude of the causal effects among the traits would be possible.

Statistical comparisons between SMM, FRM and ICM

The values of DIC obtained under SMM, FRM and ICM were 36744.107, 36709.141 and 36678.551, respectively. Fitting two SEM-based models including FRM and ICM resulted in lower DIC than the corresponding SMM; generally implied the more plausibility of considering causal effects than ignoring these corresponding causal effects. DIC value obtained under ICM was lower than that of obtained under FRM.

The SMM, FRM and ICM were also compared in terms of the predictive ability of models based on average mean square of error (MSE) and average Pearson's correlation coefficient between observed and predicted records (r(y,ŷ)) of traits under these models (Table 3). For all the studied traits, the lowest MSE and the highest r(y,ŷ)values were obtained under ICM. The reductions of MSE and increase of r(y,ŷ) values under ICM relative to SMM were more apparent for 6MW, 9MW and YW than BW and WW. Considering the comparative measures, FRM was performed better than SMM but not than ICM. Therefore, ICM was considered for inferring causal relationships among the traits and the corresponding genetic evaluation of the traits.

Table 3
Predictive ability for the studied traits under the different multivariate studied models.

Traits a	Model ¥
	SMM		FRM		ICM
	b MSE	b r(y,ŷ)	b MSE	b r(y,ŷ)	b MSE	b r(y,ŷ)
BW	0.404	0.426	0.402	0.428	0.399	0.433
WW	14.702	0.648	12.840	0.695	12.190	0.697
6MW	18.078	0.705	9.980	0.850	9.867	0.851
9MW	22.142	0.746	8.641	0.909	8.497	0.910
YW	34.113	0.740	13.003	0.909	12.862	0.910

• ^aBW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight. ^b MSE: mean square error, r(y,ŷ)= Pearson correlation between observed and predicted values. ^¥ SMM: Standard multivariate model, FRM: Fully recursive multivariate model, ICM: IC-algorithm based multivariate mode.

AmouPosht-e Masari et al. (2018) compared three multivariate models including standard multivariate, temporal recursive multivariate and fully recursive multivariate for genetic evaluation of growth traits in Lori-Bakhtiari sheep breed, temporal recursive multivariate model favored over other models in terms of lower DIC. Mokhtari et al. (2018) compared recursive and standard multivariate models for genetic evaluation of early growth traits in Raeini Cashmere goat including birth weight, weaning weight and six-month weight in terms of DIC, MSE and r(y,ŷ) and found lower DIC, lower MSE (for weaning weight and six-month weight) and higher r(y, ŷ) (for weaning weight and six-month weight) under recursive multivariate model than standard one. They concluded that considering causal relationships among the studied growth traits in Raeini goat may provide a better explanation to biological relationships among the studied traits. In a previous study, Maturana et al. (2010) considered causal relationships among calving traits including gestation length (as parent trait), calving difficulty and stillbirth in first-parity US Holsteins under three recursive multivariate models and compared them with standard multivariate model, which ignored causal relationships, in terms of mean square error and Pearson^'s correlation coefficient between predicted and observed records. They generally concluded that models included causal relationships performed better than standard multivariate model with lower mean square error and higher Pearson correlation coefficient between predicted and observed records.

Recursive effects

Applying ICM features of posterior means and posterior standard deviations (PSD) for structural coefficients among studied body weight traits of Kurdi sheep with 99% highest posterior density (HPD) intervals are presented in Table 4. All the estimated structural coefficients were positive and highly significant, 99% HPD intervals did not include zero.

The estimates for direct causal effects of BW on WW, of WW on 6MW, of 6MW on 9MW and of 9MW on YW were increases of 1.478, 0.737, 0.776 and 0.929 kg per increase of one kg in BW, WW, 6MW and 9MW of Kurdi lambs, respectively. Furthermore, indirect causal effects from BW on 6MW (mediated via WW), on 9MW (mediated via WW and 6MW) and on YW (mediated via WW, 6MW and 9MW) were also detected as 1.089, 0.845 and 0.785kg, respectively. Mokhtari et al. (2018) studied causal relationships among early growth traits including BW, WW and 6MW in Raeini Cashmere goat by fitting a fully recursive multivariate models. The estimates of direct causal recursive effects from BW on WW, BW on 6MW and WW on 6MW were obtained as 1.94, 2.48 and 1.03 kg per increase in parent trait in each case.

Table 4
Posterior means ± posterior standard deviation (PSD) for the structural coefficients under ICM.

Causal effect a	Mean ± PSD b	99% HPD intervalb
BW-WW	1.478±0.249	0.838-2.117
WW-6MW	0.737±0.040	0.634-0.840
6MW-9MW	0.776±0.028	0.694-0.840
9MW-YW	0.929±0.032	0.847-1.011

• ^aBW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight. ^b99% HPD intervals did not include zero.

Genetic parameter estimates

Features of the posterior means and PSD for direct heritability of all the studied traits, maternal heritability (for BW and WW) and pe² (for BW and WW) under ICM are shown in Table 5. These estimates were statistically significant (99% HPD intervals did not include zero). It should be pointed out that parameters estimated are pertaining to standard equivalent and are comparable with those of obtained under standard model in the literature.

Table 5
Posterior means ± posterior standard deviation (PSD) for direct and maternal heritability and ratio of maternal permanent environmental variance to phenotypic variance estimates for the studied traits.

Traits a	bh2d ± PSD	bh2m ± PSD	bpe2 ± PSD
BW	0.21±0.05	0.13±0.03	0.13±0.03
WW	0.38±0.05	0.09±0.02	-
6MW	0.24±0.05	-	0.04±0.01
9MW	0.23±0.05	-	0.08±0.02
YW	0.31±0.08	-	-

• ^aBW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight. ^bh²_d: direct heritability; h²_m: maternal heritability, pe²: ratio of maternal permanent environmental effects to phenotypic variance.

Mokhtari, Rashidi, & Mohammadi (2008) estimated direct heritability values of 0.32, 0.03 and 0.15 for 6MW, 9MW and YW of Kermani lambs. In another study, Mohammadi, Rashidi, Mokhtari, & Esmailizadeh (2010) studied genetic parameters for growth traits in Sanjabi sheep and estimated values of 0.09, 0.15, 0.09, 0.19 and 0.11 for direct heritability of BW, WW, 6MW, 9MW and YW, respectively which were generally lower than the corresponding estimated values in the present study. Jafaroghli, Rashidi, Mokhtari, and Mirzamohammadi (2013) reported direct heritablity estimates of 0.34, 0.09, 0.06, 0.12 and 0.06 for for BW, WW, 6MW, 9MW and YW of Baluchi sheep which were generally lower than estimates obtained in the present study, except for BW. Jafari, Hashemi, Darvishzadeh, and Manafiazar (2014) estimated direct heritablity values of 0.27, 0.23, 0.41, 0.40 and 0.31 for BW, WW, 6MW, 9MW and YW of Makuie sheep breed, respectively. AmouPosht-e Masari et al. (2018) fitted fully recursive multivariate model on growth traits in Lori-Bakhtiari sheep and estimated direct heritability values of 0.29, 0.18 and 0.16 for BW, WW and 6MW, respectively.

The role of maternal additive genetic effects was only decisive on BW and WW, disappeared at later ages until body weight at yearling. Maternal heritability estimated values for BW (0.13) and WW (0.09) in the present were lower than those of direct heritability. Abegaz et al. (2005) obtained maternal heritability estimates of 0.10 and 0.15 for BW and WW in Horro sheep which were in general agreement with estimates obtained in the present study.

Mohammadi et al. (2010) reported maternal heritability estimates of 0.14 and 0.24 for BW and WW in Sanjabi sheep. Rashidi et al. (2008) reported value of 0.24 for maternal heritability of BW in Kermani sheep which was higher than the corresponding estimated value in the present study. AmouPosht-e Masari et al. (2018) estimated maternal heritability values of 0.06 and 0.11 for BW and WW, respectively in Lori-Bakhtiari sheep breed under a temporal recursive multivariate model which were in general agreement with corresponding estimated values in the present study.

Features of the posterior means and PSD for the ratio of permanent maternal environmental variance to phenotypic variance estimates for BW (0.13), 6MW (0.04) and 9MW (0.08) were statistically significant (99% HPD intervals did not include zero). AmouPosht-e Masari et al. (2018) reported pe² estimates of 0.10, 0.14 and 0.06 for BW, WW and 6MW, respectively in Lori-Bakhtiari sheep breed under a temporal recursive multivariate model which were in general agreement with corresponding estimated values in the present study.

Features of the posterior means and PSD for direct genetic, phenotypic, maternal genetic (between BW and WW), maternal permanent environmental (for BW-6MW, BW-9MW and 6MW-9MW) and residual correlations are shown in Table 6.

The Estimates on direct genetic and phenotypic correlations among the studied body weight traits were positive and statistically significant (95% HPD interval did not include zero) with direct genetic correlations higher than those of the corresponding phenotypic ones. Such trend was also reported by Abegaz et al. (2005) in Horro sheep. The existence of such positive and direct genetic correlations among the body weight traits indicate that improving any of the traits considered would bring positive direct genetic and phenotypic gains for others. Direct genetic and phenotypic correlations of BW with other studied body weight traits of Kurdi sheep were lower than those of estimated among WW, 6MW, 9MW and YW. Direct genetic correlation estimates range from 0.35 (BW-9MW) to 0.93 (6MW-9MW) and phenotypic ones from 0.16 (BW-YW) to 0.77 (6MW-9MW). Direct genetic and phenotypic correlation estimates for BW-WW, BW-6MW and WW-6MW in Lori Bakhtiari sheep breed were (0.47 and 0.30), (0.49 and 0.40) and (0.97 and 0.97), respectively under a temporal recursive model (AmouPosht-e Masari et al., 2018) which were in general agreement with the corresponding values in the present study. Estimated direct genetic and phenotypic correlations among the body weight traits were in general agreement with the corresponding estimates reported by Abegaz et al. (2005) and Mohammadi et al. (2010) in Horro and Sanjabi sheep breeds, respectively. Legarra and Robert-Granie (2006) pointed out that by ignoring causal relationship between the traits, while that relationship is hold biologically, genetic correlation would be overestimated and by including causal relationship between traits, while that relationship does not hold biologically, genetic correlation would be underestimated.

Table 6
Posterior means ± posterior standard deviation (PSD) for direct genetic, maternal genetic, maternal permanent environment, phenotypic and residual correlation estimates between the studied traits.

Pair traits a	brd ± PSD	brp ± PSD	brm ± PSD	brpe ± PSD	bre ± PSD
BW-WW	0.39±0.13	0.30±0.04	0.46±0.15		0.26±0.01
BW-6MW	0.49±0.12	0.26±0.03	-	0.93±0.10	0.15±0.01
BW-9MW	0.35±0.15	0.20±0.03	-	0.63±018	0.11±0.01
BW-YW	0.49±0.13	0.16±0.03	-	-	0.08±0.01
WW-6MW	0.83±0.05	0.59±0.03	-	-	0.56±0.01
WW-9MW	0.80±0.06	0.48±0.03	-	-	0.40±0.01
WW-YW	0.77±0.07	0.42±0.03	-	-	0.29±0.04
6MW-9MW	0.93±0.03	0.77±0.01	-	0.78±0.11	0.72±0.01
6MW-YW	0.81±0.05	0.58±0.01	-		0.53±0.01
9MW-YW	0.89±0.07	0.74±0.02	-		0.73±0.01

• ^aBW: birth weight; WW: weaning weight; 6MW: Six-month weight; 9MW: Nine-month weight; YW: Yearling weight. ^br_d = direct genetic correlation, r_p= phenotypic correlation, r_m = maternal genetic correlation, r_pe= ratio of maternal permanent environmental variance to phenotypic variance correlation.

Maternal genetic correlation estimated between BW and WW (0.46) were in accordance with that of reported by Mohammadi et al. (2010) in Sanjabi sheep breed (0.53) and lower that the corresponding estimated value in Horro sheep (0.77) by Abegaz et al. (2005). Estimated value for maternal permanent environmental correlations among BW, 6MW and 9MW were medium to high. Similar to us, AmouPosht-e Masari et al. (2018) reported maternal permanent environmental correlations of 0.54 (BW-WW and BW-6MW) and 0.99 (WW-6MW) in Lori Bakhtiari sheep under a temporal recursive model.

In the present study, residual correlations between BW and other body weight traits were positive and low, ranged from 0.08 (BW-YW) to 0.26 (BW-WW). Residual correlations among other traits were medium to high and ranged from 0.29 for WW-YW to 0.73 for 9MW-YW. Similar trend was also observed by Mohammadi et al. (2010) for estimated residual correlations among body weight traits of Sanjabi sheep.

Conclusion

Inferring relationships among the studied growth traits in Kurdi sheep could help to identify development of the growth process from birth to yearling age. Applying IC algorithm, a model with temporal recursive causal relationships detected among the studied growth traits in Kurdi sheep which favored on fully recursive and standard multivariate models in terms of lower DIC. Furthermore, IC-based multivariate model showed more superiority on other two tested models in terms of lower MSE and higher Pearson^'s correlation coefficient between observed and predicted records of the studied growth traits. Significant direct causal effects detected from BW on WW, WW on 6MW, 6MW on 9MW and 9MW on YW. The plausibility of considering causal effects for genetic evaluation of growth traits in Kurdi sheep was evident in the present study. But such effects are not generally considered for developing the sheep breeding systems which may be due to this fact that SEMs are relatively new models in animal breeding context and their application in the breeding systems may require more investigation.

Acknowledgements

The authors wish to thank all Breeding Station staff of Kurdi sheep which involved in data collection and maintaining the flock through the years

References

• Abegaz, S., Van Wyk, J. B., & Olivier, J. J. (2005). Model comparisons and genetic and environmental parameter estimates of growth and the Kleiber ratio in Horro sheep. South African Journal of Animal Science, 35(1),30-40. doi: 10.4314/sajas.v35i1.4046
  » https://doi.org/10.4314/sajas.v35i1.4046
• Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control,19(6), 716-723. doi: 10.1109/TAC.1974.1100705
  » https://doi.org/10.1109/TAC.1974.1100705
• AmouPosht-e Masari, H., Hafezian, S. H., Arpanahi, R. A., Mokhtari, M. S., & RahimiMianji, G. (2018). Estimation of genetic parameters and genetic trends for growth traits in Lori Bakhtiari sheep using structural equation models. Animal Production Research, 7,83-96.
• Boujenane, I., & Kansari, J. (2002). Estimates of (co)variances due to direct and maternal effects for body weights in Timahdite sheep. Animal Science, 74(3), 409-414. doi: 10.1017/S1357729800052553
  » https://doi.org/10.1017/S1357729800052553
• Bouwman, A. C., Valente, B. D., Janss, L. L. G., Bovenhuis, H., & Rosa, G. J. M. (2014). Exploring causal networks of bovine milk fatty acids in a multivariate mixed model context. Genetic Selection Evolution, 46(1), 2. doi: 10.1186/1297-9686-46-2
  » https://doi.org/10.1186/1297-9686-46-2
• Gianola, D., & Sorensen, D. (2004). Quantitative genetic models for describing simultaneous and recursive relationships between phenotypes. Genetics,167(3),1407-1424.
• Inoue, K., Valente, B. D., Shoji, N., Honda, T., Oyama, K., & Rosa, G. J. M. (2016). Inferring phenotypic causal structures among meat quality traits and the application of a structural equation model in Japanese Black cattle. Journal Animal Science, 94, 4133-4142. doi: 10.2527/jas.2016-0554
  » https://doi.org/10.2527/jas.2016-0554
• Jafari, S., Hashemi, A., Darvishzadeh, R., & Manafiazar, G. (2016). Genetic parameters of live body weight, body measurements, greasy fleece weight, and reproduction traits in Makuie sheep breed. Spanish Journal of Agricultural Research, 12(3), 653-663. doi: 10.5424/sjar/2014123-4564
  » https://doi.org/10.5424/sjar/2014123-4564
• Jafaroghli, M., Rashidi, A., Mokhtari, M. S., & Mirzamohammadi, E. (2013). Estimation of genetic parameters for body weight traits in Baluchi sheep. Journal of Livestock Science and Technology, 1(2), 28-88.
• Maturana, E. L., Campos, G., Wu, X. L., Gianola, D., Weigel, K. A., & Rosa, G. J. M. (2010). Modeling relationships between calving traits: a comparison between standard and recursive mixed models. Genetic Selection Evolution, 42(1),1. doi: 10.1186/1297-9686-42-1
  » https://doi.org/10.1186/1297-9686-42-1
• Maturana, E., Legarra, A., Varona, L., & Ugarte, E. (2007). Analysis of fertility and Dystocia in Holsteins using recursive models to handle censored and categorical data. Journal Dairy Science, 90(4), 2012-2024. doi: 10.3168/jds.2005-442
  » https://doi.org/10.3168/jds.2005-442
• Meyer, K. (2007). WOMBAT-A tool for mixed model analyses in quantitative genetics by REML. Journal of Zhejiang University SCIENCE B, 8(11), 815-821. doi: 10.1631/jzus.2007.B0815
  » https://doi.org/10.1631/jzus.2007.B0815
• Misztal, I., Tsuruta, S., Lourenso, D. A. L., Masuda, Y., Aguilar, I., Legarra, A., & Vitezica, Z. (2018). Manual for BLUPF90 family of programs Retrieved from: http://nce.ads.uga.edu/wiki/doku.php?id=documentation
  » http://nce.ads.uga.edu/wiki/doku.php?id=documentation
• Mohammadi, Y., Rashidi, A., Mokhtari, M. S., & Esmailizadeh, A. K. (2010). Quantitative genetic analysis of growth traits and Kleiber ratios in Sanjabi sheep. Small Ruminant Research,93(2-3),88-93. doi: 10.1016/j.smallrumres.2010.05.005
  » https://doi.org/10.1016/j.smallrumres.2010.05.005
• Mokhtari, M. S., Moghbeli Damaneh, M., & Arpanahi, R. A. (2018). The application of recursive multivariate model for genetic evaluation of early growth traits in Raeini Chasmere goat: A comparison with standard multivariate model. Small Ruminant Research,165, 54-61. doi: 10.1016/j.smallrumres.2018.06.008
  » https://doi.org/10.1016/j.smallrumres.2018.06.008
• Mokhtari, M. S., Rashidi, A., & Mohammadi, Y. (2008). Estimation of genetic parameters for post-weaning traits of Kermani sheep. Small Ruminant Research, 80(1), 22-27. doi: 10.1016/j.smallrumres.2008.08.002
  » https://doi.org/10.1016/j.smallrumres.2008.08.002
• Pearl, J. (2000). Causality: Models, Reasoning and Inference Cambridge, UK: Cambridge University Press.
• R Development Core Team (2009). R: A Language and Environment for Statistical Computing Vienna, AU: R Foundation for Statistical Computing.
• Rashidi, A., Mokhtari, M. S., Jahanshahi, A. S., & Abadi, M. R. M. (2008). Genetic parameter estimates of pre-weaning growth traits in Kermani sheep. Small Ruminant Research, 74(1), 165-171. doi: 10.1016/j.smallrumres.2007.06.004
  » https://doi.org/10.1016/j.smallrumres.2007.06.004
• Rosa, G. J. M., Valente, B. D., Campos, G.,Wu, X. L., Gianola, D., & Silva, M. (2011). AInferring causal phenotype networks using structural equation models. Genetic Selection Evolution, 43, 6. doi: 10.1186/1297-9686-43-6
  » https://doi.org/10.1186/1297-9686-43-6
• Saghi, D. A., & Shahdadi, A. R. (2017). Estimates of genetic and phenotypic parameters for reproductive traits in Iranian native Kurdi sheep. Acta Scientiarum Animal Science, 39(3), 323-328. doi: 10.4025/actascianimsci.v39i3.35378
  » https://doi.org/10.4025/actascianimsci.v39i3.35378
• Saghi, D. A., Shahdadi, A. R., Borzalabad, F. K., & Mohammadi, K. (2018). Estimates of covariance functions for growth of Kurdi sheep in Iran using random regression models. Small Ruminant Research,162, 69-76.
• Shahdadi, A. R., & Saghi, D. A. (2016). Estimating genetic parameters of body weight traits in Kourdi sheep. Iranian Journal of Applied Animal Science, 6(3), 657-663.
• Sorensen, D. A., & Gianola, D. (2002). Likelihood, Bayesian and MCMC methods in quantitative genetics New York, NY: Springer.
• Statistical Analysis System [SAS]. (2004). SAS Users’ Guide, Version 9.1 Cary, NC: SAS Institute Inc.
• Tosh, J. J., & Kemp, R. A. (1994). Estimation of variance components for lamb weights in three sheep populations. Journal of Animal Science, 72(5),1184-1190. doi: 10.2527/1994.7251184x
  » https://doi.org/10.2527/1994.7251184x
• Valente, B. D., & Rosa, G. J. M. (2013). Mixed effects structural equation models and phenotypic causal networks. In C. Gondro (Ed.), Genome-Wide Association Studies and Genomic Prediction Totowa, NJ: Humana Press.
• Valente, B. D., Rosa, G. J. M., Campos, G., Gianola, D., & Silva, M. A. (2010). Searching for recursive causal structures in multivariate quantitative genetics mixed models. Genetics, 185(2),633-644. doi: 10.1534/genetics.109.112979
  » https://doi.org/10.1534/genetics.109.112979
• Valente, B. D., Rosa, G. J. M., Gianola, D., Wu, X. L., & Weigel, K. (2013). Is structural equation modeling advantageous for the genetic improvement of multiple traits. Genetics, 194(3), 561-572. doi: 10.1534/genetics.113.151209
  » https://doi.org/10.1534/genetics.113.151209
• Valente, B. D., Rosa, G. J. M., Silva, M. A., Teixeira, R. B., & Torres, R. A. (2011). Searching for phenotypic causal networks involving complex traits: an application to European quail. Genetic Selection Evolution, 43, 37.
• Wright, S. (1921). Correlation and causation. Journal of Agricultural Research, 20(7), 557-585.
• Wright, S. (1934). An analysis of variability in number of digits in an inbred strain of guinea pigs. Genetics, 19, 506-536.

Publication Dates

• Publication in this collection
  06 July 2020
• Date of issue
  2020

History

• Received
  22 July 2019
• Accepted
  26 Feb 2020