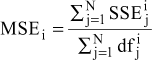Resumos
Dados de altura da cernelha e idade de 26 cavalos Pantaneiros, obtidos, na maioria, do nascimento até 36 meses, foram ajustados aos modelos de respostas não-lineares de Brody, Richards, Gompertz, Logístico, Weibull e Morgan-Mercer-Flodin. Estes seis modelos matemáticos foram comparados com o uso de uma medida de curvatura média e do erro médio quadrático combinado. O modelo de Weibull foi escolhido. A assíntota desta curva representa a altura esperada na maturidade. Os machos apresentaram um valor maior desta quantidade do que as fêmeas. O índice de maturidade, contudo, é maior para as fêmeas. Observou-se uma indicação de associação negativa entre altura na maturidade e índice de maturidade somente nas fêmeas. Tais resultados indicam que as fêmeas amadurecem mais cedo. Após testes de normalidade e homogeneidade de variância, as diferenças entre sexos foram analisadas com o uso do teste-t. Somente a altura da cernelha ao nascimento apresentou diferença significativa.
curvatura; crescimento; relações altura-idade
Height at withers data mostly from birth to 36 months of age of 26 Pantaneiro horses were used to fit Brody, Richards, Gompertz, Logistic, Weibull and Morgan-Mercer-Flodin nonlinear response functions. Based on measures of average curvature and combined mean square error, the Weibull model was chosen. The asymptote of this curve, representing the average height at maturity, was higher for males than females. The maturity index, however, was more elevated for females than males. There was indication of a negative association between the maturity index and height at maturity only for females. These results indicate that females mature earlier. After checking for normality and homogeneity of variances within groups (sex) the analysis investigated sex differences via t-tests. A significant difference was detected only for height at birth.
curvature; growth; height-age relationships
ESTATÍSTICA
Using nonlinear models to describe height growth curves in pantaneiro horses1 1 Accepted for publication on February 18, 1999. 2 Zootecnist, M.Sc., Embrapa-Centro de Pesquisa Agropecuária do Pantanal (CPAP), Caixa Postal 109, CEP 79320-900 Corumbá, MS, Brazil. E-mail: sasantos@cpap.embrapa.br 3 Statistician, Ph.D., Embrapa-Secretaria de Administração Estratégica (SEA), CEP 70770-901 Brasília, DF, Brazil. 4 Statistician, Dep. de Estatística, Universidade de Brasília, CEP 70910-900 Brasília, DF, Brazil. 5 Veterinarian, M.Sc., Embrapa-CPAP.
Sandra Aparecida Santos2 1 Accepted for publication on February 18, 1999. 2 Zootecnist, M.Sc., Embrapa-Centro de Pesquisa Agropecuária do Pantanal (CPAP), Caixa Postal 109, CEP 79320-900 Corumbá, MS, Brazil. E-mail: sasantos@cpap.embrapa.br 3 Statistician, Ph.D., Embrapa-Secretaria de Administração Estratégica (SEA), CEP 70770-901 Brasília, DF, Brazil. 4 Statistician, Dep. de Estatística, Universidade de Brasília, CEP 70910-900 Brasília, DF, Brazil. 5 Veterinarian, M.Sc., Embrapa-CPAP. , Geraldo da Silva e Souza3 1 Accepted for publication on February 18, 1999. 2 Zootecnist, M.Sc., Embrapa-Centro de Pesquisa Agropecuária do Pantanal (CPAP), Caixa Postal 109, CEP 79320-900 Corumbá, MS, Brazil. E-mail: sasantos@cpap.embrapa.br 3 Statistician, Ph.D., Embrapa-Secretaria de Administração Estratégica (SEA), CEP 70770-901 Brasília, DF, Brazil. 4 Statistician, Dep. de Estatística, Universidade de Brasília, CEP 70910-900 Brasília, DF, Brazil. 5 Veterinarian, M.Sc., Embrapa-CPAP. , Marcos Ruben de Oliveira4 1 Accepted for publication on February 18, 1999. 2 Zootecnist, M.Sc., Embrapa-Centro de Pesquisa Agropecuária do Pantanal (CPAP), Caixa Postal 109, CEP 79320-900 Corumbá, MS, Brazil. E-mail: sasantos@cpap.embrapa.br 3 Statistician, Ph.D., Embrapa-Secretaria de Administração Estratégica (SEA), CEP 70770-901 Brasília, DF, Brazil. 4 Statistician, Dep. de Estatística, Universidade de Brasília, CEP 70910-900 Brasília, DF, Brazil. 5 Veterinarian, M.Sc., Embrapa-CPAP. and José Robson Sereno5 1 Accepted for publication on February 18, 1999. 2 Zootecnist, M.Sc., Embrapa-Centro de Pesquisa Agropecuária do Pantanal (CPAP), Caixa Postal 109, CEP 79320-900 Corumbá, MS, Brazil. E-mail: sasantos@cpap.embrapa.br 3 Statistician, Ph.D., Embrapa-Secretaria de Administração Estratégica (SEA), CEP 70770-901 Brasília, DF, Brazil. 4 Statistician, Dep. de Estatística, Universidade de Brasília, CEP 70910-900 Brasília, DF, Brazil. 5 Veterinarian, M.Sc., Embrapa-CPAP.
ABSTRACT - Height at withers data mostly from birth to 36 months of age of 26 Pantaneiro horses were used to fit Brody, Richards, Gompertz, Logistic, Weibull and Morgan-Mercer-Flodin nonlinear response functions. Based on measures of average curvature and combined mean square error, the Weibull model was chosen. The asymptote of this curve, representing the average height at maturity, was higher for males than females. The maturity index, however, was more elevated for females than males. There was indication of a negative association between the maturity index and height at maturity only for females. These results indicate that females mature earlier. After checking for normality and homogeneity of variances within groups (sex) the analysis investigated sex differences via t-tests. A significant difference was detected only for height at birth.
Index terms: curvature, growth, height-age relationships.
Uso de modelos não-lineares para o ajuste de curvas de crescimento de cavalos pantaneiros
RESUMO - Dados de altura da cernelha e idade de 26 cavalos Pantaneiros, obtidos, na maioria, do nascimento até 36 meses, foram ajustados aos modelos de respostas não-lineares de Brody, Richards, Gompertz, Logístico, Weibull e Morgan-Mercer-Flodin. Estes seis modelos matemáticos foram comparados com o uso de uma medida de curvatura média e do erro médio quadrático combinado. O modelo de Weibull foi escolhido. A assíntota desta curva representa a altura esperada na maturidade. Os machos apresentaram um valor maior desta quantidade do que as fêmeas. O índice de maturidade, contudo, é maior para as fêmeas. Observou-se uma indicação de associação negativa entre altura na maturidade e índice de maturidade somente nas fêmeas. Tais resultados indicam que as fêmeas amadurecem mais cedo. Após testes de normalidade e homogeneidade de variância, as diferenças entre sexos foram analisadas com o uso do teste-t. Somente a altura da cernelha ao nascimento apresentou diferença significativa.
Termos para indexação: curvatura, crescimento, relações altura-idade.
INTRODUCTION
Populations can be characterized by their growth patterns but growth is a complex biological phenomenon with no adequately defined direct measure (Robinson, 1976). Hyperplasy (an increase in cell number) and hypertrophy (an increase in cell size) determine to what extent an animal increases in weight and size, and development determines the shape of an animal along with various organ functions. The study of animal growth is often described as the integration of all aspects of animal science including nutrition, genetics or animal breeding, physiology and meat science (Trenkle & Marple, 1983).
Growth curves reflect the lifetime interrelationships between an individual's inherent impulse to grow and mature all body parts and the environment in which these impulses are expressed. Knowledge of the growth curve is important to all animal scientists, regardless of specialization, who are concerned with the effects of their research and recommendations on lifetime production efficiency (Fitzhugh, 1976). Growth curves have been characterized by plotting measures of size (weight, height, width) against age. The use of regression models to describe growth condenses the information contained in a time series into a few biologically interpretable parameters (Eisen, 1974). Several models are available for this purpose and experimental comparisons are needed to assist in the choice of the most appropriate model (Brown et al., 1976). Mathematical nonlinear models to describe growth have been developed by Brody (1945), Richards (1959), Nelder (1961), and Ratkowsky (1983). These models have been used in beef cattle to describe weight-age relationships (Brown et al., 1972, 1976; Duarte, 1975; De Nise & Brinks, 1985; Nobre et al., 1987) but have not been used in horses.
The majority of the studies on horse growth are based on weight, height, chest girth and cannon bone (Green, 1961, 1969, 1976; Hintz et al., 1979; Santos, 1989). Of these measurements, height has more practical interest because it is required for the purpose of description and classification of horses, while weight is more a measure of the physical condition of the animal (Reed & Dunn, 1977; Hickman & Collis, 1984). According to Trenkle & Marple (1983) growth curves can be of significant value in future selection programs and in the study of the energetics of growth.
The purpose of the present study was to choose, among alternative nonlinear response functions, the best model in regard to goodness of fit, computational ease, and validity of large sample approximations in small samples. The sex and age effects on the growth of Pantaneiro horses in the Brazilian Pantanal were also evaluated.
MATERIAL AND METHODS
The data on measurements of height at withers were obtained for 14 males and 12 females at Nhumirim farm, Nhecolândia sub-region, Brazilian Pantanal, during the period from 1990 to 1995. Monthly height at withers measures were taken until 3 months of age and at 6, 12, 18, 24, and 36 months of age. Eight animals were also measured at 48 months of age. Most measurements were taken by the same person, however variation can occur due mainly to the levelness of the ground. Height at withers is a vertical distance from the ground to the highest protruding thoracic vertebrae. The measurements were taken with a 'hipometer'. Only horses with 1080 or more days of age were included in the analyses. Breeding seasons lasted last four months (November to February) and three sires were used in this period. The animals were maintained in native pasture and they received common salt ad libitum. A growth curve was fit to each animal. Six nonlinear response functions were selected for curve fitting: 1. Brody growth function: Ht = a(1-be-kt); 2. Richards growth function: Ht = a(1-be-kt)m; 3. Gompertz growth function: Ht = a exp{-exp(b-kt)}; 4. Logistic growth function:  . Weibull growth function:
. Weibull growth function:  ; 6. Morgan-Mercer-Flodin - MMF growth function:
; 6. Morgan-Mercer-Flodin - MMF growth function:  . These models are described in detail in Ratkowsky (1983) where one may also find handy techniques to obtain initial parameter estimates in each case. They are all used to fit the same type of data. The ordinary least squares estimates, for each animal and each model, were computed using the modified Gauss-Newton method of Hartley (1961) and PROC NLIN of SAS (1990). In regard to these fits five animals (four males and one female) showed atypical behavior and were excluded from further analyses. In this context the number of animals under investigation was reduced to 21 (10 males and 11 females). For the excluded horses in all instances but one either convergence was not obtained or it was very slow for some of the models. In the exception case convergence results were sound but the parameter estimates were far different (outliers) suggesting the presence of a distinct population. The model MMF did not converge for any of the animals. This is the only instance were we can report a serious computational difficulty.
. These models are described in detail in Ratkowsky (1983) where one may also find handy techniques to obtain initial parameter estimates in each case. They are all used to fit the same type of data. The ordinary least squares estimates, for each animal and each model, were computed using the modified Gauss-Newton method of Hartley (1961) and PROC NLIN of SAS (1990). In regard to these fits five animals (four males and one female) showed atypical behavior and were excluded from further analyses. In this context the number of animals under investigation was reduced to 21 (10 males and 11 females). For the excluded horses in all instances but one either convergence was not obtained or it was very slow for some of the models. In the exception case convergence results were sound but the parameter estimates were far different (outliers) suggesting the presence of a distinct population. The model MMF did not converge for any of the animals. This is the only instance were we can report a serious computational difficulty.
A common characteristic of all growth models above is that they share at least two biologically relevant parameters. The asymptote a representing average size at maturity and the parameter k. The latter is a function of the ratio of the maximum growth rate to mature size. It is commonly referred as maturity index. For the Weibull model, the parameter d can also be seen as a maturity index. The smaller and positive are its values the slower will be the approximation of the corresponding growth curves to their respective asymptotes. We attach no general special meaning to band to m, the latter in the case of the Richards response. They both influence the speed at which the asymptote is attained. With a positive association between band k, a large maturity index will imply a large b and the combined effect will be a fast maturity rate. Another parametric function of biological importance is the height at birth, which is given by a(1-b), a(1-b)m, a exp {-eb}, a/(1+eb) and a-b, respectively, for models 1, 2, 3, 4, 5 e 6.
Two diagnostic measures were used to choose among the alternative response functions. A measure of nonlinearity (intrinsic curvature) and a measure of goodness of fit. Curvature measures have been introduced in the statistical literature by Beale (1960) and extended by Bates & Watts (1980). The concept is extensively used by Ratkowsky (1983) to choose among alternative models and to assess the validity of large sample statistical procedures in small samples. It is a diagnostic tool intended to measure departures from linearity. The more linear a model is the more likely it is to show desirable computational and distributional properties for nonlinear least square estimates. Small curvatures imply that biases in the estimation of parameters and their variances will be negligible and the corresponding statistical distributions will be close to normal. Curvatures appear in two kinds: intrinsic curvature, a property of the response function in use, and parametric curvature, a property of the particular parametrization used in the definition of the response function. A large parametric curvature may be reduced by a suitable reparametrization of the model function. A large intrinsic curvature, on the other hand, may put in jeopardy the use of asymptotic theory in a particular application. The concepts are presented in full detail in Seber & Wild (1989) were one may also find the computing algorithm suggested by Bates & Watts (1980). Oliveira (1996) developed a SAS macro to implement the Bates and Watts procedure which is used in this study to compute intrinsic curvatures.
The measure of goodness of fit used was the combined mean squares error (MSE).
For model i,
where N is the number of animals,  is the residual sum of squares resulting from the fit of model i to the jth animal, and
is the residual sum of squares resulting from the fit of model i to the jth animal, and  is the corresponding error degrees of freedom.
is the corresponding error degrees of freedom.
The presence of sex and age differences was investigated via t-tests on the parameters, exploring the replication pattern imbedded in the experiment.
RESULTS AND DISCUSSION
Table 1 shows the average value of the intrinsic curvature and the combined mean square error for each of the nonlinear response functions considered in this study. The two models with best prediction power (smallest combined mean square error) are Richards and Weibull. Between these, the Weibull model showed a considerable lower level of nonlinearity. It is worth to mention that the coefficients of determination for the Weibull fits range from 0.988 to 0.999. The average value for females is 0.994 and for males 0.993. Since the Richards response function has an essentially equivalent prediction power, similar results apply for the corresponding model.
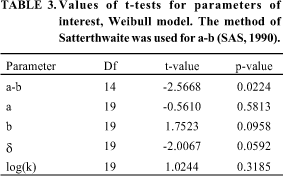
Table 2 shows average values of parameter estimates for the Weibull model for each sex. Confidence intervals were evaluated under the assumption that parameter estimates represent samples from normal populations centered at the corresponding true population values. This approach is convenient to deal with the correlation problem imbedded in the study of growth curves. Although observations taken on the same individual may be correlated, parameters, obtained for different individuals, inherit the independence of the sampling scheme. Only the maturity index k fails to pass Shapiro-Wilks normality test (SAS, 1990). However log(k) has a distribution that can be fairly closely approximated by a normal. In this context it was computed a confidence interval for log(k). The interval was inverted to set up confidence bounds for k.
The asymptote a, the average height at maturity, was only 1.2 cm higher for males than for females (Table 2). The maturity index k was larger for females than males (1.472 and 1.360, respectively). The differences were not markedly significant since, as shown in Table 3, the corresponding hypothesis of equality cannot be rejected. The Weibull curves for each sex, based on the average values of Table 2, are shown in Fig. 1.
Only height at birth fails the test of homogeneity of variances.
Table 3 reports the findings. Only a-b (height at birth) showed a real sex difference. Females had a lesser height at birth than males. This did not agree with the findings of Reed & Dunn (1977) for the Arabian horse. The parameters d and bshowed marginal significance. Females showed a smaller value of d and a larger value of b.
The relationship between asymptotic growth level and maturity may be assessed from Table 4 where Spearman (rank) correlation coefficients are shown. There is a negative association between a and k (and d) only for females.
The larger maturity index estimate and the negative association between a and k observed for the female group indicate that females mature earlier than males. This is confirmed by a smaller value of d (and a larger b) for the female group and the significant negative association of this parameter with the asymptote. A further indication the females mature earlier, following De Nise & Brinks (1985), is the significant smaller height at birth for females and the positive association between b and k for the group. According to Brown et al. (1972) different mature size may or may not represent different patterns of growth. In the present study, the mature height obtained for males was bellow the average (142 cm ) obtained for Pantaneiro males registered in the Association ABCCP. For females the opposite was observed (the Association average is 137 cm ). Both values are within the confidence limits of Table 3 but the value for males is quite close to the upper bound. There are two explanations for this. Firstly the males registered with the association are selected animals and secondly the males observed in the present study may not have reached maturity. Reed & Dunn (1977) studying Arabian horses observed that the mature height at withers for females was achieved by 48 months of age whereas males grew another 1.0 cm from 48 to 60 months of age. Therefore, in order to have a good fit to asymptotic height, 60 months of age is necessary for males. In this context is also important to emphasize that the animals we observed were maintained in native pastures without a feed supplement.
CONCLUSIONS
1. The Weibull response function is the best parametric model to fit height-age data for Pantaneiro horses.
2. The male response curve slightly dominates.
ACKNOWLEDGEMENTS
To Maria Cristina Medeiros Mazza; for the assistance to Roberto Rondon and Márcio Silva and others; for the collaboration in the collection of the data.
REFERENCES
- BATES, D.M.; WATTS, D.G. Relative curvature measures of nonlinearity. Journal of the Royal Statistical Society, Series B, v.42, p.1-25, 1980.
- BEALE, E.M.L. Confidence regions in non-linear estimation. Journal of the Royal Statistical Society, Series B, v.22, p.41-76, 1960.
- BRODY, S. Bioenergetics and growth. New York: Reinhold, 1945. p.491-661.
- BROWN, J.E.; BROWN, C.J.; BUTTS, W.T. A discussion of the genetic aspects of weight mature weight and rate of maturing in Hereford and Angus cattle. Journal of Animal Science, v.34, n.4, p.525-537, 1972.
- BROWN, J.E.; FITZHUGH, H.; CARTWRIGHT, T.C. A comparison of nonlinear models for describing weight-age relationships in cattle. Journal of Animal Science, v.42, n.4, p.810-818, 1976.
- DE NISE, R.S.K.; BRINKS, J.S. Genetic and environmental aspects of the growth curve parameters in beef cows. Journal of Animal Science, v.61, n.6, p.1431-1440, 1985.
- DUARTE, F.A.M. Estudo da curva de crescimento de animais de raça 'Nelore' (Bos taurusindicus) através de cinco modelos estocásticos Ribeirão Preto: USP, 1975. 284p. Tese de Mestrado.
- EISEN, E.J. Results of growth curve analyses in mice and rats. Journal of Animal Science, v.42, n.4, p.1008-1023, 1974.
- FITZHUGH, H. Analysis of growth curves and strategies for alterating their shape. Journal of Animal Science, v.42, n.4, p.1036-1051, 1976.
- GREEN, D.A. A review of studies on the growth rate of the horse. British Veterinary Journal, v.117, p.181-191, 1961.
- GREEN, D.A. A study of growth rate in thoroughbred foals. British Veterinary Journal, v.125, p.539-545, 1969.
- GREEN, D.A. Growth rate in thoroughbred yearlings and two years olds. Equine Veterinary Journal, v.8, n.3, p.133-134, 1976.
- HARTLEY, H.O. The modified Gauss-Newton method for the fitting of nonlinear regression functions by least squares. Technometrics, v.3, p.269-280, 1961.
- HICKMAN, J.; COLLIS, C. Measurement of horses. The Veterinary Record, v.114, p.491-493, 1984.
- HINTZ, H.F.; HINTZ, R.L.; VANVIECK, L.D. Growth rate of thoroughbred. Effects of age of dam, year and month of birth, and sex of foal. Journal of Animal Science, v.48, n.3, p.480-487, 1979.
- NELDER, J.A. The fitting of a generalization of the logistic curve. Biometrics, v.17, p.89-110, 1961.
- NOBRE, P.R.C.; ROSA, A.N.; SILVA, L.C.; EVANGELISTA, S.R.M. Curvas de crescimento de gado Nelore ajustadas para diferentes frequências de pesagens. Pesquisa Agropecuária Brasileira, Brasília, v.22, n.9/10, p.1027-1037, 1987.
- OLIVEIRA, M.R. Medidas de diagnóstico em regressão não linear. Brasília: UnB, Departamento de Estatística, 1996. 35p. Relatório de Estágio Supervisionado.
- RATKOWSKY, D.A. Nonlinear regression modeling: a unified practical approach. New York: Marcel Dekker, 1983. 276p.
- REED, K.R.; DUNN, N.K. Growth and development of the Arabian horse. In: EQUINE NUTRITION AND PHYSIOLOGY SYMPOSIUM, 1977, St. Louis. Proceedings... Philadelphia: ENP Society, 1977. p.76-98.
- RICHARDS, F.J. A flexible growth function for empirical use. Journal of Experimental Biology, v.10, p.290-300, 1959.
- ROBINSON, D.W. Growth patterns in swine. Journal of Animal Science, v.42, n.4, p.1024-1035, 1976.
- SANTOS, S.A. Estudo sobre algumas características de crescimento de cavalos Brasileiro de Hipismo produzidos no haras Pioneiro Piracicaba: USP, 1989. 90p. Dissertação de Mestrado.
- SAS INSTITUTE. SAS user's guide: statistics, version 6. 4.ed. Cary, NC, 1990. v.2, 1686p.
- SEBER, G.A.F.; WILD, C.J. Nonlinear regression. New York: John Wiley, 1989. 768p.
- TRENKLE, A.; MARPLE, D.N. Growth and development of meat animals. Journal of Animal Science, v.57, n.2, p.273-283, 1983.
Datas de Publicação
-
Publicação nesta coleção
14 Out 2011 -
Data do Fascículo
Jul 1999
Histórico
-
Recebido
18 Fev 1999