Abstract
Most mining decisions are based on models estimated/simulated given the information obtained from samples. During the exploration stage, samples are commonly taken using diamond drill holes which are accurate and precise. These samples are considered hard data. In the production stage, new samples are added. These last are cheaper and more abundant than the drill hole samples, but imprecise and are here named as soft data. Usually hard and soft data are not sampled at the same locations, they form a heterotopic dataset. This article proposes a framework for geostatistical simulation with completely heterotopic soft data. The simulation proceeds in two steps. First, the variable of interest at the locations where soft data are available is simulated. The local conditional distributions built at these locations consider both hard and soft data and are obtained using simple cokriging with the intrinsic coregionalization model. Second, the variable of interest in the entire simulation grid using the original and previously simulated values at soft data locations is simulated. The results show that the information from soft data improved both the accuracy and precision of the simulated models. The proposed framework is illustrated by a case study with data obtained from an underground copper mine.
Keywords:
local probability distribution; completely heterotopic; geostatistical simulations; data integration
1. Introduction
Decisions in mining operations are generally based on estimated/simulated grade models. The information used to build these models comes from samples obtained from various sources. At every stage of a mining project, more samples are collected and used to update the models and reduce their uncertainty.
During the exploration stage, the samples are mostly diamond drill cores, which are accurate and precise, but expensive and scarce. These samples are considered error-free and are denoted hard data. At the production phase, additional samples are obtained from blast hole drilling fragments (dust) or channel samples. Compared to the diamond drill samples, these samples are cheaper and more abundant, but they have a non-negligible sampling error and are denoted soft data. Usually, soft and hard data are not sampled at the same locations.
Classical approaches to integrate different data sources in geostatistical simulations are generally known as co-simulation. The sequential Gaussian co-simulation (Verly 1993VERLY, G. W. Sequential Gaussian cosimulation: a simulation method integrating several types of information. In: SOARES, A. (ed.). Geostatistics Troia’92. Dordrecht: Springer, 1993. v. 1, p. 543-554.) is one of the first workflows and is an expansion of the original sequential Gaussian simulation (Isaaks 1990ISAAKS, E. H. The application of Monte Carlo methods to the analysis of spatially correlated data. Palo Alto, Ca: Stanford University, 1990.) to consider multiple variables and their correlations. The sequential Gaussian co-simulation uses simple cokriging to integrate different data. The relationships between the different types of data are described by the linear model of coregionalization (LMC) (Journel and Huijbregts 1978JOURNEL, A. G.; HUIJBREGTS, C. J. Mining geostatistics. London: Academic press, 1978.; Goovaerts 1997GOOVAERTS, P. Geostatistics for natural resources evaluation. Oxford: Oxford University Press, 1997.; Wackernagel 2003WACKERNAGEL, H. Multivariate geostatistics: an introduction with applications. 3rd. ed. [S. l.]: Springer, 2003. 404 p.). Oliveira et al. (2020OLIVEIRA, C. A. S. et al. Use of heterotopic secondary data in geostatistics using covariance tables. Applied Earth Science, v. 129, n. 1, p. 15-26, 2020.) proposed a methodology for geostatistical co-simulation that does not require the LMC. The integration of data of different types is based on covariance tables (direct and cross), which describe the spatial continuity of the data. The main limitation of this technique is that the secondary data must be densely sampled.
The problem of sequential Gaussian co-simulation is that fitting the LMC is often a tedious and challenging task. This task is even more complicated when the hard and soft data are heterotopic and have different and irregular sampling spacing. In this case, the experimental cross-variograms cannot be calculated, so cross-covariograms or correlograms must be used. In addition, these experimental cross-correlograms may be very sensitive to their calculation parameters, such as lag spacing and tolerances.
Another problem is that the sequential Gaussian co-simulation requires solving the cokriging system at all the nodes of the simulation grid whose search neighborhood includes secondary data. The resolution of the cokriging system may slow the simulation process, if the search neighborhood includes many samples. Using many samples in the search neighborhood is recommended for geostatistical simulations, since it aids in reducing the uncertainty.
One approach for simulation of multiple correlated variables without modeling the LMC is to simulate the variables hierarchically (Journel and Almeida 1994JOURNEL, A. G. Geostatistics for conditional simulation of ore bodies. Economic Geology, v. 69, n. 5, p. 673-687, 1974.) using collocated cokriging with a Markov model of coregionalization (Almeida and Journel 1994ALMEIDA, A. S.; JOURNEL, A. G. Joint simulation of multiple variables with a Markov-type coregionalization model. Mathematical Geology, v. 26, n. 5, p. 565-588, 1994.; Journel 1999JOURNEL, A. G. Markov models for cross-covariances. Mathematical Geology, v. 31, n. 8, p. 955-964, 1999.). In the Markov models, the cross-variogram models are proportional to the variogram models of either the hard or soft data (Shmaryan and Journel 1999SHMARYAN, L. E.; JOURNEL, A. G. Two Markov models and their application. Mathematical geology, v. 31, n. 8, p. 965-988, 1999.). This approach requires that the soft data be available at all locations of the simulation grid. Otherwise, the soft data may be simulated first to populate the simulation grid. Then, the hard data or primary variable is simulated using the collocated secondary/soft datum with collocated cokriging.
The problem of simulating the variables hierarchically with collocated cokriging is that the variance of the primary simulated variable is too high (Journel and Deutsch 1998DEUTSCH, C. V.; JOURNEL, A. G. GSLIB - Geostatistical software library and user’s guide. 2nd. New York: Oxford University Press, 1998.). In this context, Babak and Deutsch (2009BABAK, O.; DEUTSCH, C. V. An intrinsic model of coregionalization that solves variance inflation in collocated cokriging. Computers & geosciences, v. 35, n. 3, p. 603-614, 2009.) proposed a method that solves the variance inflation of collocated cokriging. The method is called intrinsic collocated cokriging (ICCK) and consists of simulating with cokriging using the secondary data at the node being simulated and at the locations of the primary data. The authors used the intrinsic coregionalization model (ICM) to define the direct and cross-variogram models. The intrinsic coregionalization model (ICM) is a particular case of the LMC, where all the direct and cross-variograms are proportional to one basic variogram model (Goovaerts 1997GOOVAERTS, P. Geostatistics for natural resources evaluation. Oxford: Oxford University Press, 1997.). For instance, all direct and cross-variograms are obtained by multiplying a basic variogram model by a rescaling factor. The basic variogram model used by Babak and Deutsch (2009)BABAK, O.; DEUTSCH, C. V. An intrinsic model of coregionalization that solves variance inflation in collocated cokriging. Computers & geosciences, v. 35, n. 3, p. 603-614, 2009. for the ICM was the variogram model of the primary variable. Thus, ICCK requires fitting only the variogram model of the primary variable.
In this study, we adapted the ICCK (Babak and Deutsch 2009BABAK, O.; DEUTSCH, C. V. An intrinsic model of coregionalization that solves variance inflation in collocated cokriging. Computers & geosciences, v. 35, n. 3, p. 603-614, 2009.) to the situation of complete heterotopy between the hard and soft data. These authors showed a case study with exhaustive secondary data. In this case, the secondary data are available at the locations of the primary data, and the use of ICCK is straightforward. This article considers the situation where the secondary data are not at the locations of the primary data.
Intrinsic collocated cokriging requires the coefficient of correlation between the variables, whose calculation is not direct when the data are completely heterotopic. To obtain the coefficient of correlation between the variables, we extrapolated the experimental cross-correlogram values until the distance of zero (Minnitt and Deutsch 2014MINNITT, R. C. A.; DEUTSCHE, C. V. Cokriging for optimal mineral resource estimates in mining operations. Journal of the Southern African Institute of Mining and Metallurgy, v. 114, n. 3, p. 189-189, 2014.). There are other ways to obtain the relationship between different variables in the case of heterotopic data. Myers (1982MYERS, D. E. Matrix formulation of co-kriging. Journal of the International Association for Mathematical Geology, v. 14, n. 3, p. 249-257, 1982.) and Cressie (1991)CRESSSIE, N. A. C. Statistics for spatial data. Hoboken, New Jersey: John Wiley & Sons, 1991. proposed one generalization of the variogram to compute the cross variance between variables called as pseudo cross variogram. Some authors discuss the limitations of the pseudo cross variogram when the variables are measured at different support and units (Papritz et al. 1994PAPRITZ, A.; FLÜHLER, H. Temporal change of spatially autocorrelated soil properties: optimal estimation by cokriging. Geoderma, v. 62, n. 1-3, p. 29-43, 1994.; Papritz and Fluhler 1993PAPRITZ, A.; KÜNSCH, H. R.; WEBSTER, R. On the pseudo cross-variogram. Mathematical Geology, v. 25, n. 8, p. 1015-1026, 1993.). Cressie and Wikle (1997)CRESSIE, N.; WIKLE, C. K. The variance-based cross-variogram: you can add apples and oranges. Mathematical Geology, v. 30, n. 7, p. 789-799, 1998. have a different standpoint. They believe that in cokriging estimates with variance-based cross-variograms, the variables can be measure with a different mean and scale. Foehn et al. (2018FOEHN, A. et al. Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments. Journal of Hydrology, v. 563, p. 1092-1110, 2018) used the pseudo cross variogram to compute the linear model corregionalization to develop a methodology called regression cokriging in heterotopic data applied in meteorological data
When the dataset is heterotopic, Barnett and Deutsch (2015BARNETT, R. M.; DEUTSCH, C. V. Multivariate imputation of unequally sampled geological variables. Mathematical Geosciences, v. 47, n. 7, p. 791-817, 2015.) and Silva and Deutsch (2018SILVA, D. S. F.; DEUTSCH, C. V. Multivariate data imputation using Gaussian mixture models. Spatial statistics, v. 27, p. 74-90, 2018.) proposed multiple imputation (MI) to integrate secondary data into geostatistical simulations. The main idea of MI is to perform the geostatistical simulations in two steps. The first step is to simulate the primary variables at the locations of the secondary data. The result is a series of different datasets. The second step consists of performing geostatistical simulation in the simulation grid using the different datasets generated at the first step as conditioning information. Each generated dataset conditions one realization. This simulation at the second step is performed using simple kriging. This approach is efficient since it requires solving the cokriging system only at the locations of the secondary data. The main drawback of this approach is that only the collocated secondary datum is used.
Similar to Barnett and Deutsch (2015BARNETT, R. M.; DEUTSCH, C. V. Multivariate imputation of unequally sampled geological variables. Mathematical Geosciences, v. 47, n. 7, p. 791-817, 2015.) and Silva and Deutsch (2018SILVA, D. S. F.; DEUTSCH, C. V. Multivariate data imputation using Gaussian mixture models. Spatial statistics, v. 27, p. 74-90, 2018.), Soares et al. (2017SOARES, A.; NUNES, R.; AZEVEDO, L. Integration of uncertain data in geostatistical modelling. Mathematical Geosciences, v. 49, n. 2, p. 253-273, 2017.) Neves et al. (2018), and Narciso et al. (2019NARCISO, J. et al. A Geostatistical Simulation of a Mineral Deposit using Uncertain Experimental Data. Minerals, v. 9, n. 4, p. 247, 2019.) also simulated at the locations of the soft data before simulating in the simulation grid. At the location of the soft data, Soares et al. (2017)SOARES, A.; NUNES, R.; AZEVEDO, L. Integration of uncertain data in geostatistical modelling. Mathematical Geosciences, v. 49, n. 2, p. 253-273, 2017., Neves et al. (2018) and Narciso et al. (2019)NARCISO, J. et al. A Geostatistical Simulation of a Mineral Deposit using Uncertain Experimental Data. Minerals, v. 9, n. 4, p. 247, 2019. used direct sequential simulation (Soares 2001) with local probability distributions. The collocated soft datum informed the local histogram used for direct sequential simulation. The result was a set of datasets that conditioned the simulations in the simulation grid, which were performed with DSS and a global histogram. Araujo et al. (2019ARAÚJO, C. P.; BASSANI, M. A. A.; COSTA, J. F. C. L. Geostatistical simulation with heterotopic soft data without the LMC. In: MUELLER, C. et al. (ed.). Mining Goes Digital. London: CRC Press, 2019. p. 125-133.) proposed Bayesian Updating (Deutsch and Zanon 2004DEUTSCH, C. V.; ZANON, S. D. Direct prediction of reservoir performance with Bayesian updating under a multivariate Gaussian model. In: CANADIAN INTERNATIONAL PETROLEUM CONFERENCE, 2004, Calgary, Alberta. Proceedings […]. Calgary: Petroleum Society of Canada, 2004.; Doyen et al. 1996DOYEN, P. M. et al. Seismic porosity mapping in the Ekofisk field using a new form of collocated cokriging. In: SPE ANNUAL TECHNICAL CONFERENCE AND EXHIBITION, 1996, Denver, Colorado. Proceedings […]. [S. l.]: Society of Petroleum Engineers, 1996.; Neufeld and Deutsch 2006NEUFELD, C.; DEUTSCH, C. V. Data integration with non-parametric bayesian updating. CCG Annual Report, v. 8, n. 105, 2006.) to build the local probability distribution at each location where a soft datum is available and sequential Gaussian simulation to complete the remaining grid nodes. The main drawback of these methods is that only one collocated soft datum combined with hard data is used to condition the simulations.
Cuba et al. (2012CUBA, M.; LEUANGTHONG, O.; ORTIZ, J. Transferring sampling errors into geostatistical modelling. Journal of the Southern African Institute of Mining and Metallurgy, v. 112, n. 11, p. 971-983, 2012.) proposed a method to combine data with different errors. The method builds a conditional distribution at the location of the soft data using only the neighborhood samples removing the sample with error. The Gibbs sampler algorithm is used to sample from this conditional distribution. The simulated values are kept if they satisfy statistical requirements (variogram and histogram). Maleki Tehrani et al. (2013TEHRANI, M. A. M.; ASGHARI, O.; EMERY, X. Simulation of mineral grades and classification of mineral resources by using hard and soft conditioning data: application to Sungun porphyry copper deposit. Arabian Journal of Geosciences, v. 6, n. 10, p. 3773-3781, 2013.) showed a method to consider both hard and soft data in geostatistical simulation. The original soft data consisted of geological information (rock type description), while the hard data consisted of copper grades. The first step was to build a local Cumulative Distribution Function (CDF) of grades in these soft data locations. The local CDFs followed a Gaussian distribution, whose means and variances correspond to the cokriging estimates and variances. The conditioning information for cokriging consisted of the original hard data and the soft geological data. The second step consisted of simulating a set of values at these local CDFs using the matrix decomposition method (Alabert 1987ALABERT, F. The practice of fast conditional simulations through the LU decomposition of the covariance matrix. Mathematical Geology, v. 19, n. 5, p. 369-386, 1987.). Finally, these simulated values were combined with the original hard data to condition the simulations that occur over the entire study area. Some approaches based on Kalman filters, to integrate soft data to update short-term mining plans, improved production control in mineral resource extraction (Benndorf and Jansen, 2017BENNDORF, J.; JANSEN, J. D. Recent developments in closed-loop approaches for real-time mining and petroleum extraction. Mathematical Geosciences, v. 49, n. 3, p. 277-306, 2017.; Wambeke and Benndorf, 2017WAMBEKE, T.; BENNDORF, J. A simulation-based geostatistical approach to real-time reconciliation of the grade control model. Mathematical Geosciences, v. 49, n. 1, p. 1-37, 2017.).
Different from the other proposals presented herein, we present a method that uses all the hard and soft data available in the local vicinity of a soft datum to condition the simulations. To the authors’ knowledge, the method has not been applied before. Similar to other approaches (Cuba, 2012CUBA, M.; LEUANGTHONG, O.; ORTIZ, J. Transferring sampling errors into geostatistical modelling. Journal of the Southern African Institute of Mining and Metallurgy, v. 112, n. 11, p. 971-983, 2012.; Barnett and Deutsch (2015BARNETT, R. M.; DEUTSCH, C. V. Multivariate imputation of unequally sampled geological variables. Mathematical Geosciences, v. 47, n. 7, p. 791-817, 2015.); Silva and Deutsch (2018SILVA, D. S. F.; DEUTSCH, C. V. Multivariate data imputation using Gaussian mixture models. Spatial statistics, v. 27, p. 74-90, 2018.); Soares et al. (2017SOARES, A.; NUNES, R.; AZEVEDO, L. Integration of uncertain data in geostatistical modelling. Mathematical Geosciences, v. 49, n. 2, p. 253-273, 2017.); Neves et al. (2018); Narciso et al. (2019NARCISO, J. et al. A Geostatistical Simulation of a Mineral Deposit using Uncertain Experimental Data. Minerals, v. 9, n. 4, p. 247, 2019.) and Araujo et al. (2019ARAÚJO, C. P.; BASSANI, M. A. A.; COSTA, J. F. C. L. Geostatistical simulation with heterotopic soft data without the LMC. In: MUELLER, C. et al. (ed.). Mining Goes Digital. London: CRC Press, 2019. p. 125-133.)), we start by generating a series of datasets at the location of the soft datum. The generation of the datasets is performed by p-field simulation (Srivastava 1992SRIVASTAVA, R. M. Reservoir characterization with probability field simulation. In: SPE ANNUAL TECHNICAL CONFERENCE AND EXHIBITION, 1992, Washington, D.C. Proceedings […]. [S. l.]: Society of Petroleum Engineers, 1992.). The conditional cumulative distribution functions required for p-field simulation were built with MultiGaussian cokriging using all the hard and soft data inside the search neighborhood. P-field simulation is used due to its simplicity and flexibility, since the local distribution may be obtained from any source of information.
The direct and cross-covariances required for cokriging were obtained by the intrinsic coregionalization model (ICM), so that all the variograms are proportional to the variogram of the primary variable. The ICM requires the coefficient of correlation, which was obtained by extrapolating the experimental cross-correlogram (Minnitt and Deutsch 2014MINNITT, R. C. A.; DEUTSCHE, C. V. Cokriging for optimal mineral resource estimates in mining operations. Journal of the Southern African Institute of Mining and Metallurgy, v. 114, n. 3, p. 189-189, 2014.). This cokriging is similar to the ICCK used by Babak and Deutsch (2009BABAK, O.; DEUTSCH, C. V. An intrinsic model of coregionalization that solves variance inflation in collocated cokriging. Computers & geosciences, v. 35, n. 3, p. 603-614, 2009.).
The result of the p-field simulation is a set of datasets that are used to condition the simulations in the simulation grid. The simulations at the remaining grid nodes were performed afterwards with turning bands simulation (Journel and Huijbregts 1978JOURNEL, A. G.; HUIJBREGTS, C. J. Mining geostatistics. London: Academic press, 1978.). Simple kriging was used to condition the turning band simulations. Although the p-field simulation may generate some artifacts (Pyrcz and Deutsch 2001PYRCZ, M. J.; DEUTSCH, C. V. Two artifacts of probability field simulation. Mathematical geology, v. 33, n. 7, p. 775-799, 2001.; Ortiz 2003ORTIZ, J. M. Correcting variogram reproduction of p-field simulation. CCG Annual Report, v. 5, n. 103, 2003.), the number of locations simulated with p-field simulation is negligible compared to the number of locations simulated with turning bands. The result is that the final geostatistical models do not present the artifacts of p-field simulation.
The advantages of the workflow proposed are the following: (i) only the spatial continuity model of the hard data is required; the uncertainty of soft data is accounted for in the geostatistical models, (ii) it is computationally efficient, and (iii) all the available soft data are considered. An underground mine case study illustrates the methodology proposed.
2. Methodology
This article proposes a methodology to integrate heterotopic soft data into geostatistical models. Soft data are referred to herein as values of the same variable of hard data but with attached uncertainty (imprecise). The methodology is presented in Figure 1 and listed below:
-
Build the Conditional Cumulative Distribution Function (CCDF) at soft data locations using MultiGaussian cokriging. For this, local simple cokriging estimation was performed at the soft data locations using all hard and soft data within the search neighborhood. The local CCDF has a Gaussian distribution with mean and variance equal to the simple cokriging mean and variance, respectively. The Intrinsic Coregionalization Model (ICM) was used, so all direct and cross-variograms are proportional to the variogram model of hard data.
-
Generate a spatially correlated grid of random numbers in the interval [0, 1] via unconditional simulation. This is the main idea of p-field simulation (Srivastava 1992SRIVASTAVA, R. M. Reservoir characterization with probability field simulation. In: SPE ANNUAL TECHNICAL CONFERENCE AND EXHIBITION, 1992, Washington, D.C. Proceedings […]. [S. l.]: Society of Petroleum Engineers, 1992.; Froidevaux 1993FROIDEVAUX, R. Probability field simulation. In: SOARES, A. (ed.). Geostatistics Tróia’92. Dordrecht: Springer, 1993. v. 1, p. 73-83.). These values were generated by unconditional geostatistical simulation using the variogram model of hard data. N scenarios were generated
-
Draw a value from the CCDF built-in (i) using the random number obtained in (ii) at this soft data location.
-
Repeat (ii) and (iii) at all soft data locations.
-
Combine original hard data with a realization at all soft data locations and proceed with simulation of the remaining grid.
-
Repeat (ii) to (v) for a new realization.
The methodology described above in six steps (i to vi) is herein known as Pfield/Tbsim.
3. Case study
3.1 Data presentation
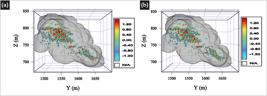
This study uses data from an underground copper mine. The geological domain considered was sampled by two different types of data (hard and soft data). Figure 2 shows a data location map. The hard data (Figure 2a) were collected using diamond drill holes, and are considered accurate and precise, but have a large sample spacing. There are 470 samples with an average sampling spacing of 10 × 10 m. The soft data (Figure 2b) comprise 1473 values sampled by channels. The soft data are imprecise and inaccurate because errors are incorporated during the sampling process. The average space between soft data values is 3 × 3 m.
Copper underground mine data locations used in this work in ZY vertical section - a) hard data location b) soft data location; the gray area corresponds to the geological domain.
Table 1 shows the global statistics for the declustered dataset, using cell declustering (Deustch and Journel,1998DEUTSCH, C. V.; JOURNEL, A. G. GSLIB - Geostatistical software library and user’s guide. 2nd. New York: Oxford University Press, 1998.) which will be combined to build a grade model: hard data (Cu_DDH) with good quality and sparse and soft data (Cu_Channels) with poor quality and abundant. The mean and standard deviation are respectively 73.25% and 89.68 %, higher than that of the hard data. These large differences indicate that soft data was collected in the vein area (Figure 2a and 2b), where the high grades are located. To check for bias and imprecision in the soft data, both the hard and soft data must be investigated at the same domain.
Table 2 shows the main statistics of the declustered dataset of the samples that are a maximum of 3 m apart (quasi-collocated). This was obtained by assigning the soft datum value to the nearest hard datum location whose distance was less than 3 m. We assume that the hard data (Cu_DDH) are unbiased and precise. The mean and standard deviation of the soft (Cu_Channels) data are respectively 5.25% and 8.50% lower than that of the hard data. These differences indicate that soft data is biased and imprecise.
Figure 3 shows the univariate Gaussian histograms of the hard (Figure 3a) and soft (Figure 3b) data. The data were transformed d by the normal transformation (Deutsch and Journel, 1998DEUTSCH, C. V.; JOURNEL, A. G. GSLIB - Geostatistical software library and user’s guide. 2nd. New York: Oxford University Press, 1998.). The data are transformed as the simulation techniques used assume that the data follow a multivariate Gaussian distribution. The histograms show that the data after transformation are standard normal (zero mean, unit variance) for both variables.
Histogram in Nscore unit for variables: a) primary variable (hard) (Cu_DDH) b) secondary (soft) variable (Cu_Channels).
3.1.1 Bivariate statistics and spatial continuity
In order to compute correlation in a completely heterotopic dataset (the hard and soft data are never at the same location), the experimental cross-correlogram plot (Figure 4) was used to project the cross-correlogram to zero h and infer the correlation among data (Minnitt and Deutsch 2014MINNITT, R. C. A.; DEUTSCHE, C. V. Cokriging for optimal mineral resource estimates in mining operations. Journal of the Southern African Institute of Mining and Metallurgy, v. 114, n. 3, p. 189-189, 2014.). The results (blue line) indicate a considerable correlation of approximately 0.90.
Cross-correlogram for different lags between hard and soft data, correlation fit (red line) and extrapolation (blue line).
The spatial continuity model of the hard data used in this case was defined using standardized variogram models. (Eq. 1), and this model is defined by two spherical (Sph) structures. The major, intermediate and vertical directions are called h1, h2 and h3, respectively. This model was used for p-field and turning bands simulations.
3.2 p-field simulation
MultiGaussian cokriging was used to build the local CDFs which are used afterwards to draw local realizations using p-field simulation. The local CCDF is Gaussian where the mean is the cokriging estimate and the variance is the cokriging variance. The cross-covariances for the cokriging were obtained by the intrinsic coregionalization model. Figure 5 shows the variance map of local CCDF. The variance is zero (light blue dots) at the hard data locations, as expected. At the soft data locations, the variance depends on the amount and correlation of data in the vicinity.
Variance location map of simulate data locations generate in step i) of the proposed methodology.
Figure 6 shows the location map for two realizations of the simulated data with p-field simulation. When we compare the two, the simulated values (dots symbols) are different at the soft data locations but are the same at the hard data locations (cross symbols). It means, for each new realization, there will be different simulated values comprising the data set. Fifty realizations were generated.
Example of simulate data locations generate in the ZY vertical section in each soft data location, where the symbol plus represents hard data and circles the simulated data value in the same color scale a) scenario 15 and b) scenario 16.
3.2.1 Validating simulated data
To validate the datasets generated, we checked the histogram and variograms of the datasets built with p-field simulation. Bias effect in the histograms was controlled by using cell declustering (Deustch and Journel,1998DEUTSCH, C. V.; JOURNEL, A. G. GSLIB - Geostatistical software library and user’s guide. 2nd. New York: Oxford University Press, 1998.), leading to a weighted average Cu (%) content of 2.28 (%). Figure 7 shows the cumulative histogram of the simulated datasets (black lines) and declustered hard data (red line). The mean and standard deviation of the simulated data are close to the hard data histogram. The results indicate that the distributions are similar.
Histogram of simulated data (black lines) generated compared against the hard data (Cu_DDH) histogram (red line) and simulated data (black lines).
Figure 8 shows the experimental variograms along the major, intermediate and vertical directions, where the red line represents the variogram model (Eq. 1) and the black lines represent the experimental variograms for the generated dataset. The models are similar; meaning that the inferred data (pseudo-hard) have the same spatial continuity of the hard data. The artifacts of p-field simulation are more pronounced when there are hard data to condition the simulations. In this case, the p-field was performed only at the locations of the soft data. The result is that the experimental variograms of the dataset did not show the artifacts of the p-field simulation.
Variogram reproduction of pseudo-hard and hard data (black lines), variogram model (red line): a) major direction, b) intermediate direction and c) vertical direction.
3.3 Turning bands simulation
The remaining grid nodes were simulated with the Turning Bands simulation (Matheron, 1973MATHERON, G. The intrinsic random functions and their applications. Advances in applied probability, v. 5, n. 3, p. 439-468, 1973 and Journel, 1974JOURNEL, A. G. Geostatistics for conditional simulation of ore bodies. Economic Geology, v. 69, n. 5, p. 673-687, 1974.). These simulations were conditioned to the datasets generated by p-field simulation. For each realization, a different dataset was used, which was comprised of that original hard data and simulated data set values at soft data locations. To optimize final model results with the recommendations suggested by Emery and Lantuéjoul (2006EMERY, X.; LANTUÉJOUL, C. Tbsim: A computer program for conditional simulation of three-dimensional gaussian random fields via the turning bands method. Computers & Geosciences, v. 32, n. 10, p. 1615-1628, 2006) were used. Simple kriging was used to build and obtain the mean and variance for the local CCDF. A total of one thousand lines were used for the turning bands algorithm. Fifty realizations were created with the same spatial continuity model used in p-field simulation data describe in equation 2. Finally, the simulated models were back-transformed to the space of the original units.
3.3.1 Validation models
In Figure 9, the red line represents the cumulative histogram of the declustered hard data (Cu_DDH), and the black lines are the histograms of the realizations. The plot shows good statistical reproduction of the histogram. The relative difference between mean values is 12% for the proposed methodology. The bias can occur in situations when the histogram of Cu (%) has a small amount of data, mostly in low frequency classes. Therefore, as in the proposed workflow, soft data were used with their error incorporated; the bias and imprecision of the data were not transferred to realizations.
Histogram of simulated models compared (black lines) against the hard data histogram (red lines).
Figure 10 shows the variogram reproduction by the models obtained by Pfield/Tbsim. The red line represents the variogram model (Eq. 1), and black lines represent those derived from the realizations at the major, intermediate and vertical directions. The results show the proposed methodology reproduces the spatial continuity of hard data.
Variogram reproduction by the various models obtained by Pfield/Tbsim (black lines) against variogram model of hard data (red line): a) major direction, b) intermediate direction and c) vertical direction.
3.4 Evaluating the accuracy and precision models
In order to verify whether the results obtained by the proposed framework improved the accuracy and precision of the simulations, the values of a few hard data were excluded from the dataset, and simulations were run at these locations of the excluded data (omitted for the sake of comparison using jackknife (Efron 1982EFRON, B. The jackknife, the bootstrap, and other resampling plans. [S. l.]: SIAM, 1982.). To perform the test, eight diamond drill holes (comprising 55 hard data samples, or the equivalent of 12% of the total hard data values) were excluded from the dataset. (Figure 11).
Copper underground mine data locations along a ZY plane view (blue dots: hard data; red dots: soft data; green dots: hard data excluded from the dataset; and the gray area corresponds to the geological domain).
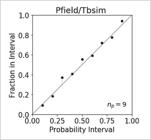
In order to check the model of uncertainty, accuracy plots were used. On this plot, the probability of a real value falling inside an interval given by simulations is checked against the number of times the real value actually fell into this interval. If the results are accurate and precise, the points of the plot are close to the 45° line. More details about accuracy plots can be found in Goovaerts (2001GOOVAERTS, P. Geostatistical modelling of uncertainty in soil science. Geoderma, v. 103, n. 1-2, p. 3-26, 2001.). Figure 12 shows the accuracy plot for the methodology investigated. The results obtained by Pfield/Tbsim show the data points closer to the 45° line, indicating that the models obtained are accurate and precise.
4. Conclusion
This article presents an approach to incorporate hard data and completely heterotopic soft data into geostatistical simulations. The simulated data generated to infer the uncertainty associated with soft data reproduced the spatial continuity and cumulative distribution (histogram) of the hard data.
The simulated data inferred by p-field simulation reproduce the distribution and spatial continuity of the hard data. The quality of the models was assessed using the accuracy plot. The results indicate the methodology proposed incorporates the uncertainty of the soft data into the final model.
For future studies, the authors suggest using the methodology in the original data space with direct sequential simulation and applying it in other case studies with variables that have different coefficients of correlation. This workflow may be an easy alternative to incorporate soft data in the simulation, since it needs few steps and the modeling of the spatial continuity only for the hard data.
Acknowledgments
The authors would like to thank the National Council for Scientific and Technological Development (CNPq) and Petrobras S.A, for supporting the Mineral Exploration and Mining Planning Research Unit (LPM) at the Federal University of Rio Grande do Sul (UFRGS).
References
- ALABERT, F. The practice of fast conditional simulations through the LU decomposition of the covariance matrix. Mathematical Geology, v. 19, n. 5, p. 369-386, 1987.
- ALMEIDA, A. S.; JOURNEL, A. G. Joint simulation of multiple variables with a Markov-type coregionalization model. Mathematical Geology, v. 26, n. 5, p. 565-588, 1994.
- ARAÚJO, C. P.; COSTA, J. F. C. L. Integration of different-quality data in short-term mining planning. Rem: Revista Escola de Minas, v. 68, n. 2, p. 221-227, 2015.
- ARAÚJO, C. P.; BASSANI, M. A. A.; COSTA, J. F. C. L. Geostatistical simulation with heterotopic soft data without the LMC. In: MUELLER, C. et al (ed.). Mining Goes Digital London: CRC Press, 2019. p. 125-133.
- BABAK, O.; DEUTSCH, C. V. An intrinsic model of coregionalization that solves variance inflation in collocated cokriging. Computers & geosciences, v. 35, n. 3, p. 603-614, 2009.
- BARNETT, R. M.; DEUTSCH, C. V. Multivariate imputation of unequally sampled geological variables. Mathematical Geosciences, v. 47, n. 7, p. 791-817, 2015.
- BENNDORF, J.; JANSEN, J. D. Recent developments in closed-loop approaches for real-time mining and petroleum extraction. Mathematical Geosciences, v. 49, n. 3, p. 277-306, 2017.
- CRESSSIE, N. A. C. Statistics for spatial data Hoboken, New Jersey: John Wiley & Sons, 1991.
- CRESSIE, N.; WIKLE, C. K. The variance-based cross-variogram: you can add apples and oranges. Mathematical Geology, v. 30, n. 7, p. 789-799, 1998.
- CUBA, M.; LEUANGTHONG, O.; ORTIZ, J. Transferring sampling errors into geostatistical modelling. Journal of the Southern African Institute of Mining and Metallurgy, v. 112, n. 11, p. 971-983, 2012.
- DEUTSCH, C. V.; JOURNEL, A. G. GSLIB - Geostatistical software library and user’s guide 2nd. New York: Oxford University Press, 1998.
- DEUTSCH, C. V.; ZANON, S. D. Direct prediction of reservoir performance with Bayesian updating under a multivariate Gaussian model. In: CANADIAN INTERNATIONAL PETROLEUM CONFERENCE, 2004, Calgary, Alberta. Proceedings […]. Calgary: Petroleum Society of Canada, 2004.
- DIMITRAKOPOULOS, R.; FARRELLY, C. T.; GODOY, M. Moving forward from traditional optimization: grade uncertainty and risk effects in open-pit design. Mining Technology, v. 111, n. 1, p. 82-88, 2002.
- DOYEN, P. M. et al. Seismic porosity mapping in the Ekofisk field using a new form of collocated cokriging. In: SPE ANNUAL TECHNICAL CONFERENCE AND EXHIBITION, 1996, Denver, Colorado. Proceedings […]. [S. l.]: Society of Petroleum Engineers, 1996.
- FOEHN, A. et al Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments. Journal of Hydrology, v. 563, p. 1092-1110, 2018
- EFRON, B. The jackknife, the bootstrap, and other resampling plans [S. l.]: SIAM, 1982.
- EMERY, X.; LANTUÉJOUL, C. Tbsim: A computer program for conditional simulation of three-dimensional gaussian random fields via the turning bands method. Computers & Geosciences, v. 32, n. 10, p. 1615-1628, 2006
- FROIDEVAUX, R. Probability field simulation. In: SOARES, A. (ed.). Geostatistics Tróia’92 Dordrecht: Springer, 1993. v. 1, p. 73-83.
- GOOVAERTS, P. Geostatistics for natural resources evaluation Oxford: Oxford University Press, 1997.
- GOOVAERTS, P. Geostatistical modelling of uncertainty in soil science. Geoderma, v. 103, n. 1-2, p. 3-26, 2001.
- ISAAKS, E. H. The application of Monte Carlo methods to the analysis of spatially correlated data Palo Alto, Ca: Stanford University, 1990.
- KLOECKNER, J. et al. Covariance table: a fast automatic spatial continuity mapping. Computers & Geosciences, v. 130, p. 94-104, 2019.
- JOURNEL, A. G. Geostatistics for conditional simulation of ore bodies. Economic Geology, v. 69, n. 5, p. 673-687, 1974.
- JOURNEL, A. G.; HUIJBREGTS, C. J. Mining geostatistics London: Academic press, 1978.
- JOURNEL, A. G. Markov models for cross-covariances. Mathematical Geology, v. 31, n. 8, p. 955-964, 1999.
- MARCOTTE, D. Fast variogram computation with FFT. Computers & Geosciences, v. 22, n. 10, p. 1175-1186, 1996.
- MATHERON, G. The intrinsic random functions and their applications. Advances in applied probability, v. 5, n. 3, p. 439-468, 1973
- MINNITT, R. C. A.; DEUTSCHE, C. V. Cokriging for optimal mineral resource estimates in mining operations. Journal of the Southern African Institute of Mining and Metallurgy, v. 114, n. 3, p. 189-189, 2014.
- MYERS, D. E. Matrix formulation of co-kriging. Journal of the International Association for Mathematical Geology, v. 14, n. 3, p. 249-257, 1982.
- NARCISO, J. et al A Geostatistical Simulation of a Mineral Deposit using Uncertain Experimental Data. Minerals, v. 9, n. 4, p. 247, 2019.
- NEUFELD, C.; DEUTSCH, C. V. Data integration with non-parametric bayesian updating. CCG Annual Report, v. 8, n. 105, 2006.
- NEVES, J. et al Updating Mining Resources with Uncertain Data. Mathematical Geosciences, v. 51, n. 7, p. 905-924, 2019.
- OLIVEIRA, C. A. S. et al Use of heterotopic secondary data in geostatistics using covariance tables. Applied Earth Science, v. 129, n. 1, p. 15-26, 2020.
- ORTIZ, J. M. Correcting variogram reproduction of p-field simulation. CCG Annual Report, v. 5, n. 103, 2003.
- PAPRITZ, A.; KÜNSCH, H. R.; WEBSTER, R. On the pseudo cross-variogram. Mathematical Geology, v. 25, n. 8, p. 1015-1026, 1993.
- PAPRITZ, A.; FLÜHLER, H. Temporal change of spatially autocorrelated soil properties: optimal estimation by cokriging. Geoderma, v. 62, n. 1-3, p. 29-43, 1994.
- PYRCZ, M. J.; DEUTSCH, C. V. Two artifacts of probability field simulation. Mathematical geology, v. 33, n. 7, p. 775-799, 2001.
- PYRCZ, M. J.; DEUTSCH, C. V. Semivariogram models based on geometric offsets. Mathematical geology, v. 38, n. 4, p. 475-488, 2006.
- SHMARYAN, L. E.; JOURNEL, A. G. Two Markov models and their application. Mathematical geology, v. 31, n. 8, p. 965-988, 1999.
- SILVA, D. S. F.; DEUTSCH, C. V. Multivariate data imputation using Gaussian mixture models. Spatial statistics, v. 27, p. 74-90, 2018.
- SOARES, A.; NUNES, R.; AZEVEDO, L. Integration of uncertain data in geostatistical modelling. Mathematical Geosciences, v. 49, n. 2, p. 253-273, 2017.
- SRIVASTAVA, R. M. Reservoir characterization with probability field simulation. In: SPE ANNUAL TECHNICAL CONFERENCE AND EXHIBITION, 1992, Washington, D.C. Proceedings […]. [S. l.]: Society of Petroleum Engineers, 1992.
- TEHRANI, M. A. M.; ASGHARI, O.; EMERY, X. Simulation of mineral grades and classification of mineral resources by using hard and soft conditioning data: application to Sungun porphyry copper deposit. Arabian Journal of Geosciences, v. 6, n. 10, p. 3773-3781, 2013.
- VERLY, G. W. Sequential Gaussian cosimulation: a simulation method integrating several types of information. In: SOARES, A. (ed.). Geostatistics Troia’92 Dordrecht: Springer, 1993. v. 1, p. 543-554.
- WACKERNAGEL, H. Multivariate geostatistics: an introduction with applications. 3rd. ed. [S. l.]: Springer, 2003. 404 p.
- WAMBEKE, T.; BENNDORF, J. A simulation-based geostatistical approach to real-time reconciliation of the grade control model. Mathematical Geosciences, v. 49, n. 1, p. 1-37, 2017.
Publication Dates
-
Publication in this collection
29 Mar 2021 -
Date of issue
Apr-Jun 2021
History
-
Received
29 June 2020 -
Accepted
12 Jan 2021