Abstract
The objective of this study is to present the formulation and applications of the optimization problem of steel-concrete composite alveolar beams. In addition to presenting the formulation, a comparative analysis of the predominant collapse modes is performed numerically via the finite element method. The optimization program was developed with the GUI platform available in Matlab 2016. Since this is a discrete problem, a Genetic Algorithm (GA) was used to solve the optimization model, implemented with the Matlab optimization toolbox. Numerical examples using finite elements model are presented to validate the solution and analyze its effectiveness, along with an assesment of the predominant collapse modes for a group of 12 beams. The results show that more efficient designs are obtained when optimization tools are applied.
Keywords:
alveolar beams; composite beam; genetic algorithm; collapse modes
1. Introduction
Steel beams with uniformly distributed web openings, also referred to as alveolar or castellated beams, have several constructive advantages. These include larger spans, lower overall cost of the structure and lower weight, if compared to beams of the same height with full webs. In fact, the increase in height is one of the main advantages of converting conventional beams into their alveolar counterparts, especially if the beam is structurally joined with a concrete slab, forming a steel-concrete composite floor system. This configuration allows an increase in the resistance of the structural system by taking advantage of certain mechanical characteristics of each material, which in this case are the compressive and tensile strengths of concrete and steel, respectively.
Some recent studies on steel alveolar beams, such as Cimadevila, Gutierrez and Rodrigues (2000CIMADEVILA, F. J. E.; GUTIERREZ, E. M.; RODRIGUEZ, J. A. V. Vigas alveoladas. Madri: Bellisco, 2000. (Biblioteca Técnica Universitaria: Estructuras, v. 3).), Silveira (2011SILVEIRA, E. G. Avaliação do comportamento de vigas alveolares de aço com ênfase nos modos de colapso por plastificação. 2011. 156 f. Dissertação (Mestrado em Engenharia Civil) - Universidade Federal de Viçosa, Viçosa, MG, 2011.), Veríssimo et al. (2012VERÍSSIMO, G. S.; VIEIRA, W. B.; SILVEIRA, E. G.; RIBEIRO, J. C. L.; PAES, J. L. R.; BEZERRA, E. M.; CASTRO E SILVA, A. L. R.; FAKURY, R. H. Dimensionamento de vigas alveolares de aço. In: CONSTRUMETAL - Congresso Latinoamericano da Construção Metálica, 2012, São Paulo. Anais […]. São Paulo: ABCEM, 2012. 17 p.) and Badke Neto, Calenzani and Ferreira (2015)BADKE NETO, A.; CALENZANI, A. F. G.; FERREIRA, W. G. Study of methodology for sizing steel and concrete beams with cellular profile. Internation Journal of Structures and Materials, v.8, p. 827-859, 2015., show advances in the numerical analysis of the aforementioned structural system.
Cimadevila, Gutierrez and Rodrigues (2000CIMADEVILA, F. J. E.; GUTIERREZ, E. M.; RODRIGUEZ, J. A. V. Vigas alveoladas. Madri: Bellisco, 2000. (Biblioteca Técnica Universitaria: Estructuras, v. 3).) developed a theoretical approach for determining resistant forces and deformations of steel alveolar beams, establishing consistent equations for the structural design of these elements.
Silveira (2011SILVEIRA, E. G. Avaliação do comportamento de vigas alveolares de aço com ênfase nos modos de colapso por plastificação. 2011. 156 f. Dissertação (Mestrado em Engenharia Civil) - Universidade Federal de Viçosa, Viçosa, MG, 2011.) performed a numerical analysis to evaluate the behavior of steel alveolar beams with emphasis on modes of collapse induced by plasticization. The author developed numerical models to represent alveolar beam sections normally used in the Brazilian market, focusing on the assessment of collapse modes and ultimate load.
Veríssimo et al. (2012VERÍSSIMO, G. S.; VIEIRA, W. B.; SILVEIRA, E. G.; RIBEIRO, J. C. L.; PAES, J. L. R.; BEZERRA, E. M.; CASTRO E SILVA, A. L. R.; FAKURY, R. H. Dimensionamento de vigas alveolares de aço. In: CONSTRUMETAL - Congresso Latinoamericano da Construção Metálica, 2012, São Paulo. Anais […]. São Paulo: ABCEM, 2012. 17 p.) presented a generalized analytical-numerical study aimed at reevaluating the behavior of alveolar beams with various geometries, including laminated I-profiles produced in Brazil as early as 2002, with the objective of proposing a design procedure.
A recent study published by Sonck and Belis (2015SONCK, D.; BELIS, J. Lateral-torsional buckling resistance of cellular beams. Journal of Constructional Steel Research, v. 105, p. 1199-128, 2015.) evaluates the behavior of cellular steel structures subjected to lateral torsional buckling. This methodology however, has yet to be evaluated for use in steel profiles manufactured in Brazil. Alternatively, Lubke, Alves and Azevedo (2017LUBKE, G. P.; ALVES, E. C.; AZEVEDO, M. S. Dimensionamento otimizado de vigas celulares de aço. Revista da Estrutura de Aço - REA, v.6, n. 1, p. 01-20, 2017.) introduced a formulation for optimization of cellular beams and performed a comparative analysis between different optimization methods. Alves and Lubke (2019)ALVES, E. C; LUBKE, G. P. Dimensionamento ótimo e análise dos modos de colapso de vigas alveolares e aço. Revista Sul-Americana de Engenharia Estrutural, v. 16, n.1, p. 38-64, 2019. presented the optimization problem and an analysis of the predominant collapse modes for castellated steel-concrete composite beams and their different failure patterns.
The Genetic Algorithm (GA) method was conceived by Holland (1992HOLLAND, J. H. A adaptation in natural and artificial systems. Cambridge: MIT Press, 1992.) based on principles of the theory of evolution proposed by Charles Darwin. Over the last decades, the method has been used to solve optimization problems with discrete variables in various areas of application. Recent noteworthy researches on the use of this method for structural optimization are listed below.
Cho, Min and Lee (2001CHO, H.; MIN, D.; LEE, K. Optimum life-cycle design of orthotropic steel deck bridges. Steel Structures, v. 1, p. 141-152, 2001.) used genetic algorithms to conduct an optimization study on the life cycle cost of bridges with orthotropic steel deck systems consisting of steel slabs with ribbed formwork. In this life cycle analysis, building and maintenance costs were considered, with adjustments in structural resistance, deflection and fatigue of the structure. The study concludes that the optimization analyses lead to a more rational, economical and safer design when compared to conventional methods.
Liu, Hammad and Itoh (1997LIU, C.; HAMMAD, A.; ITOH, Y. Multiobjective optimization of bridge deck rehabilitation using a genetic algorithm. Microcomputers in Civil Engineering, v. 12, p. 431-443, 1997.) conducted an optimization study for bridge recovery using GA, forming a model with multiple objective functions and combining the various results with Pareto's approach. The objective was to reduce the cost of bridge recovery and the degree of deterioration. The authors show that the GA presents excellent results even in a model containing multiple objectives, and with relatively short computational time.
Kripakaran and Gupta (2011KRIPAKARAN, P.; HALL, B.; GUPTA, A. A genetic algorithm for design of moment-resisting steel frames. Structural and Multidisciplinary Optimization, v. 44, n.4, p. 559-574, 2011.) developed, also in 2011, a decision support system based on GA applied to steel frames, with various connection types. The study highlights the advantages of using discrete variables with GA. This feature is explored in the software presented later herein.
Kociecki and Adeli (2015KOCIECKI, M.; ADELI, H. Shape optimization of free-form steel space-frame roof structures with complex geometries using evolutionary computing. Engineering Applications of Artificial Intelligence, v. 38, p. 168-182, 2015.) and Prendes-Gero et al. (2018)PRENDES-GERO, M. B.; BELLO-GARCÍA, A.; COZ-DÍAZ, J. J.; SUÁREZ DOMÍNGUEZ, F. J.; GARCÍA NIETO, P. J. Optimization of steel structures with one genetic algorithm according to three international building codes. Revista de La Construccion, v. 17, n. 1, p. 47-59, 2018. implemented GA for optimization of different steel structural systems in 2015 and 2018, respectively, and observed gains of around 10% when compared to non-optimized designs. Both studies also highlighted the ability to work with discrete variables when using GA as an important characteristic for obtaining good results. The authors emphasized the high suitability of the method for application in real world scenarios, made possible with the use of discrete variables.
Lima (2011LIMA, M. L. R. Otimização topológica e paramétrica de vigas de concreto armado utilizando algoritmos genéticos. 2011. 113 f. Dissertação (Mestrado em Engenharia) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2011.) developed an optimization program with a genetic algorithm for reinforced concrete beams using discrete variables to better represent the reality of structural projects. The authors conclude that the GA provides favorable results, especially in complex problems with discrete variables and constant restrictions. Moreover, results show that in 85% of the cases, optimized solutions were also optimal solutions.
Souza Jr. (2005)SOUZA JUNIOR, D. A. Otimização pelo método dos algoritmos genéticos e dimensionamento de estruturas tubulares metálicas espaciais com barras cruzadas para coberturas. 2005. 114 f. Tese (Doutorado em Engenharia Mecânica) - Faculdade de Engenharia Mecânica. Universidade Federal de Uberlândia, Uberlândia, 2005. developed a genetic algorithm to assess global mechanical behavior of spatial metallic tubular structures. Steel consumption was analyzed for various geometric configurations in order to minimize the cost of the structure.
Bilbao (2016BILBAO, H. F. X. A. Dimensionamento de absorvedores de massa sintonizada para lajes duplo T pré-fabricadas em concreto por meio de algoritmo genético. 2016. 75 f. Trabalho de Conclusão de Curso (Bacharelado em Engenharia Civil) - Universidade Federal Tecnológica do Paraná, Campo Mourão, 2016.) conducted an analysis of the optimal design of tuned mass dampers in prefabricated slabs using GA. Results were consistent with available design abacuses.
Ramos and Alves (2018RAMOS, J. R. S; ALVES, E. C. Dimensionamento otimizado de vigas mistas celulares utilizando algoritmos genéticos. In: SIMMEC - Simpósio de Mecânica Computacional, 13., 2018, Vitoria, ES. Anais […]. Vitória: ABMEC: UFES, 2018.) presented a formulation for the optimization of steel-concrete composite cellular beams, as well as a finite element analysis of predominant collapse modes.
The present article aims to present the formulation and criteria for optimizing the design of steel-concrete composite alveolar beams with the use of genetic algorithms, based on the guidelines provided by Lawson and Hicks (2011LAWSON, R. M.; HICKS, S. J. P355: Design of composite beams with large webopenings: in accordance with Eurocodes and the UK National Annexes. Chicago: Steel Construction Institute, 2011.), also described in the European design standard SCI Publication P355. A finite element analysis was performed in order to demonstrate the applicability of the formulation, along with a comparative analysis of the governing modes of collapse. A software was developed on Matlab 2016 using the embedded GUI and optimization toolboxes.
2. Problem formulation
The optimization model consists of choosing the optimal solution based on an objective function that will be minimized, in this case, the weight of the beam.
2.1 Objective function
The relevant geometric parameters chosen as the problem variables for a Peiner alveolar beam are presented in Figure 1. The objective function, called “minimize weight”, is shown in Equation (1):
where x1 is the profile height; x2 is the flange width; x3 is the flange thickness; x4 is the web thickness; k is the expansion ratio; n is the number of opening, ρa is the specific weight of steel.
2.2 Constraint functions
2.2.1 Resistance criteria
The optimization algorithm selects a specific beam as a solution provided that said beam meets the criteria of ultimate and serviceability limit states prescribed by Lawson and Hicks (2011LAWSON, R. M.; HICKS, S. J. P355: Design of composite beams with large webopenings: in accordance with Eurocodes and the UK National Annexes. Chicago: Steel Construction Institute, 2011.), adapted to suit Brazilian standard NBR 8800:2008ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8800: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios. Rio de Janeiro: ABNT, 2008.. Equations to determine design forces are given below.
2.2.1.1 Design vertical shear resistance of perforated steel section (VplRd)The design shear resistance of the perforated section is given by Equation (2).
where Aw is the sum of the shear area of the upper and lower tee sections; fy is the yield strength of profile steel; γa1 is the resistance factor equal to 1.1
2.2.2.2 Design bending resistance of the opening (M0,Rd)The plastic resistant bending moment can assume two values depending on the position of the neutral axis of the cross-section. If the axis crosses the concrete slab, the design bending moment is given by Equation (3).
Alternatively, if the neutral axis passes through the upper flange, the bending resistance is given by Equation (4)
where NbT,Rd is the resistant axial tensile force of the steel beam; hef is the effective beam height, measured from the centers of gravity of the tees; ht is the thickness of concrete slab; zT is the distance between the end of the flange and the center of gravity of upper tee; zc is the height of concrete under compression; Nc,Rd is the resistant axial compressive force of the concrete slab.
2.2.2.3 Verification of the vierendeel mechanismVierendeel bending resistance is given by the sum of the resistant local bending moments of the four corners of the opening and the local resistant bending moment due to the interaction of the upper tee with the concrete slab. Vierendeel's resistant bending moment should be greater than the difference between internal bending moments to the left and right of the opening, in accordance with Equation (5):
where Mb,NV,Rd is the reduced bending resistance of the lower tee due to coexisting shear and axial stresses; Mt,NV,Rd is the reduced bending resistance of the upper tee due to coexisting shear and axial stresses; Mvc,Rd is the local composite bending resistance due to the interaction of the superior tee with the concrete slab; VSd is the design shear force at the end of the opening with the lowest internal moment; le is the effective length of the opening, equal to 45% of its diameter.
2.2.2.4 Design longitudinal shear resistance of the web-post (Vwp,Rd)The value of the design longitudinal shear force of the web-post is given by Equation (6).
where s0 is the width of the web-post; tw is the thickness of the web.
2.2.2.5 Design bending resistance of the web-post (Mwp,Rd)The resistant bending moment of the web-post can be obtained by Equation (7).
2.2.2.6 Resistance to buckling of the web-post (Nwp,Rd)
The buckling resistance of the web-post relies on the reduction coefficient established in the compressive strength curve of ABNT NBR 8800:2008ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8800: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios. Rio de Janeiro: ABNT, 2008., which depends on the longitudinal slenderness of the element. According to Lawson and Hicks (2011LAWSON, R. M.; HICKS, S. J. P355: Design of composite beams with large webopenings: in accordance with Eurocodes and the UK National Annexes. Chicago: Steel Construction Institute, 2011.), this coefficient is given by Equation (8).
2.2.2.7 Verification of displacements on the beam
The maximum deflection resulting from a uniformly distributed load on the beam is determined according to Equation (9):
where q is the magnitude of uniformly distributed loading; l is the length of the beam; I is the equivalent moment of inertia of the perforated composite section.
2.3 Resistance constraint equationsAs presented in the previous items, this set of equations represent the constraints that the optimized solution must meet. These functions can be written in standard form according to Equations (10) through (19).
The variables included in Equations (10) to (19) are described in the previous sections. The optimal solution will be chosen from a steel profile catalogue, provided by ArcelorMittal (2016)ARCELORMITTAL. Catalogue: ACB® Alveolar beams. Long Products Sections and Merchan Bars. Available at: <http://sections.arcelormittal.com/library/product-catalogs.html>. Accessed: 03 Mar. 2016.
http://sections.arcelormittal.com/librar...
.
3. The Computational program
The program was developed in Matlab with the use of the GUI tool. Optimal design is obtained using Genetic Algorithms considering input parameters previously defined by the user. The program displays a summary of software checks, resistant and internal forces, as well as optimal design. The genetic algorithm chosen is an optimization model for discrete variables, suitable for the proposed problem, since the optimal solution is extracted from a table of commercially available profiles.
3.1 Applicability of the formulation
The demonstration of the applicability of the model proposed herein is performed by solving two examples of alveolar composite beams found in literature. The first and second examples consist of a comparative analysis between the solution proposed here and castellated composite beams presented by Brinkhus (2015BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.). The objective is to demonstrate that the proposed formulation is able to improve results regarding the weight of the profile.
3.1.1 Example A1
The first example is presented by Brinkhus (2015BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.). The author developed an excel spreadsheet to verify alveolar mixed beams of steel and concrete. For this example she used a profile W 150x18 kg/m, manufactured by Gerdau Açominas (table of profile Gerdau); this profile was expanded to become a castellated beam. The purpose of this example is, through the proposed formulation, to choose a profile, from the Gerdau profile table, that supports the same loads and geometric conditions (length of the span, effective width of concrete flange) used by Brinkhus and, after this choice compare the results. Input data for the first example presented by Brinkhus (2015)BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015. is shown in Table 1. Results are compared with those obtained by Brinkhus (2015)BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015. in Table 2 and Table 3, after the application of the optimization formulation.
Input data Brinkus(2015)BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015..
The optimization program indicated the profile W 150x13 kg/m as the optimal solution, also from Gerdau Açominas. The resistant forces obtained by Brinkhus (2015BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.) are greater than those found by the optimization program, since the cross-sectional area of the profile chosen by the author is larger than the one chosen by the program. All the resistant forces obtained with the program are greater than the internal forces induced by the loading. As such, the profile meets all the structural safety criteria and is 28% lighter than the optimal solution indicated by Brinkhus (2015)BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.. The constraint that governed the optimization process was the web amount buckling (NwpRd). The Table 8 shows other results for the beam chosen in the optimization process, with respect to resistant forces, as well as the relationship between these and acting forces.
3.1.2 Example A2
The second example follows the same pattern as the first example. The input data taken from Brinkhus (2015BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.) is shown in Table 4. In example A2 of Brinkhus (2015)BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015., a W 250x22.3 kg/m profile of Gerdau Açominas was analyzed, subjected to the loads shown in Table 5. The results are compared with those obtained with the program, in Table 6 e Table 7.
The optimization program indicated the profile W 310x21 kg/m as the optimal solution, also from Gerdau Açominas. The values of shear resistance VRd, and bending resistance in the opening region M0Rd, returned by the program, are greater than those of the profile chosen by Brinkhus (2015BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas. 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.). Alternatively, the axial resistance of the web-post, NwpRd, is smaller. The profile chosen by the optimization program features a larger height than the profile of example A2 (49 mm larger), however, the optimized profile is 5.83 % lighter than the one indicated in the reference. The constraint that governed the optimization process was the web amount buckling (NwpRd). The Table 8 shows others results for the beam chosen in the optimization process, with respect to resistant forces, as well as the relationship between these and acting forces.
3.1.3 Example 3 - Evaluation of collapse modes and numerical analysis
3.1.3.1 Evaluation of collapse modesThe collapse modes of the alveolar beams were used as restrictions for the implementation of the optimization routine. In optimal beam design, it is common for some constraints to govern the entire calculation process. In order to evaluate the predominant collapse modes in the optimization process, based on the proposed formulation, 13 beams were optimized for the loads show in Table 9. Results are presented in Figure 2.
-
a) To obtain the graphs in Figure 2, the two most predominant collapse modes were analyzed for each beam and in each optimization process. The following conclusions are drawn from the graphs: Web-post buckling was the most common collapse mode for ultimate limit state criteria. Both cellular and castellated beams presented the occurrence of this type of failure.
-
b) Beams with lengths of 8m, 9m and 10m presented flexural failure of the web-post along with buckling of this element. This is due to these modes of collapse being associated with shear forces in adjacent openings.
-
c) Beams of 6m and 7m presented flexural failure of the open region and incidence of the Vierendeel mechanism. Both modes of collapses are associated with the presence of bending moment in the opening, as a result of the Vierendeel mechanism.
-
d) The 16 m beam show the occurrence of the two modes associated with buckling of the web-post: the first due to the normal compressive force, NwpSd, and the second due to longitudinal shear force VwpSd.
In order to further verify the results obtained, a finite element analysis was conducted. The maximum stress observed in the finite element analysis is compared with the stress obtained analytically with Equation (20).
where Ms is internal moment induced by loading; Wx is bending modulus of the composite section.
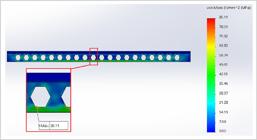
The numerical model was developed and analyzed with Solidworks Simulation software (2015)DASSAULT SYSTEMES. Solidworks Simulation Premium. [S. l.]: Dassault Systemes, 2015.. A mesh with tetrahedral solid elements with 25 mm sides and tolerance of 1.25 mm was adopted for the steel beam and the concrete slab. The elements feature 4 nodes, each with 3 degrees of freedom representing translations in the three orthogonal directions. Figure 3 shows the finite element model of the structural system. Results are exhibited in Figure 4.
Table 10 presents a comparative analysis between results from the finite element model and the optimization program.
Numerical results corroborate one of the predominant collapse modes, the flexural failure of the composite section. Overall values were close, with the largest difference being 15.97%. Maximum stresses obtained from numerical and analytical assessments fall below the yield strength of 345 MPa, adopted as the criterion for material failure.
4. Conclusions
The objective of this study was to present the formulae for design optimization of steel-concrete composite alveolar beams and their applications, as well as the results of a numerical analysis, performed to demonstrate one of the predominant collapse modes in the optimization problem.
The use of genetic algorithms resulted in improvements regarding structural weight when compared to the reference solution. Weight reduction of the optimal profile is observed in all scenarios analyzed, thus demonstrating the effectiveness of the method adopted herein.
An analysis of the collapse modes indicated that lateral buckling of the web-post is the predominant failure pattern. Furthermore, similar results are noticed between the finite element analysis and the analytical approach conducted with the optimization program developed for this research.
References
- ALVES, E. C; LUBKE, G. P. Dimensionamento ótimo e análise dos modos de colapso de vigas alveolares e aço. Revista Sul-Americana de Engenharia Estrutural, v. 16, n.1, p. 38-64, 2019.
- ARCELORMITTAL. Catalogue: ACB® Alveolar beams Long Products Sections and Merchan Bars. Available at: <http://sections.arcelormittal.com/library/product-catalogs.html>. Accessed: 03 Mar. 2016.
» http://sections.arcelormittal.com/library/product-catalogs.html - ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8800: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios. Rio de Janeiro: ABNT, 2008.
- BADKE NETO, A.; CALENZANI, A. F. G.; FERREIRA, W. G. Study of methodology for sizing steel and concrete beams with cellular profile. Internation Journal of Structures and Materials, v.8, p. 827-859, 2015.
- BILBAO, H. F. X. A. Dimensionamento de absorvedores de massa sintonizada para lajes duplo T pré-fabricadas em concreto por meio de algoritmo genético 2016. 75 f. Trabalho de Conclusão de Curso (Bacharelado em Engenharia Civil) - Universidade Federal Tecnológica do Paraná, Campo Mourão, 2016.
- BRINKHUS, R. N. Análise de Vigas Casteladas e Vigas Casteladas Mistas 2015. 168 f. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2015.
- CÂMARA NETO, J.; LANDESMANN, A.; BATISTA, E. M. Aplicação de algoritmos genéticos para. dimensionamento de vigas-mistas aço-concreto. In: CONSTRUMETAL - Congresso Latinoamericano da Construção Metálica, 2008, São Paulo. Anais […]. São Paulo: ABCEM, 2008.
- CHO, H.; MIN, D.; LEE, K. Optimum life-cycle design of orthotropic steel deck bridges. Steel Structures, v. 1, p. 141-152, 2001.
- CIMADEVILA, F. J. E.; GUTIERREZ, E. M.; RODRIGUEZ, J. A. V. Vigas alveoladas Madri: Bellisco, 2000. (Biblioteca Técnica Universitaria: Estructuras, v. 3).
- DASSAULT SYSTEMES. Solidworks Simulation Premium [S. l.]: Dassault Systemes, 2015.
- EUROPEAN COMMITEE FOR STANDARDIZATION. EN 1993-1-1: Eurocode 3: design of steel structures. Part 1-1: general rules and rules for buildings. Brussels: CEN, 1993. 93 p.
- EUROPEAN COMMITEE FOR STANDARDIZATION. EN 1994-1-1: Eurocode 4: design of composite steel and concrete structures. Part 1-1: general rules and rules for buildings. Brussels: CEN, 2004.
- HIBBLELER, R. C. Strength of materials, 7 th. ed. New Jersey: Pearson Prencice Hall. 2012.
- HOLLAND, J. H. A adaptation in natural and artificial systems Cambridge: MIT Press, 1992.
- KOCIECKI, M.; ADELI, H. Shape optimization of free-form steel space-frame roof structures with complex geometries using evolutionary computing. Engineering Applications of Artificial Intelligence, v. 38, p. 168-182, 2015.
- KRIPAKARAN, P.; HALL, B.; GUPTA, A. A genetic algorithm for design of moment-resisting steel frames. Structural and Multidisciplinary Optimization, v. 44, n.4, p. 559-574, 2011.
- KUAN-CHEN FU, F. A.; ZHAI, Y.; ZHOU, S. Optimum design of welded steel plate girder bridges using a genetic algorithm with elitism. Journal of Bridge Engineering, v. 10, n. 3, p. 291-301, 2005.
- LAWSON, R. M.; HICKS, S. J. P355: Design of composite beams with large webopenings: in accordance with Eurocodes and the UK National Annexes Chicago: Steel Construction Institute, 2011.
- LIMA, M. L. R. Otimização topológica e paramétrica de vigas de concreto armado utilizando algoritmos genéticos 2011. 113 f. Dissertação (Mestrado em Engenharia) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2011.
- LIU, C.; HAMMAD, A.; ITOH, Y. Multiobjective optimization of bridge deck rehabilitation using a genetic algorithm. Microcomputers in Civil Engineering, v. 12, p. 431-443, 1997.
- LUBKE, G. P.; ALVES, E. C.; AZEVEDO, M. S. Dimensionamento otimizado de vigas celulares de aço. Revista da Estrutura de Aço - REA, v.6, n. 1, p. 01-20, 2017.
- OLIVEIRA, L. B. Procedimento para definição das características geométricas de vigas alveolares de aço para sistemas de piso e de cobertura 2012. 147 f. Dissertação (Mestrado em Engenharia Civil) - Universidade Federal de Viçosa, Viçosa, MG, 2012.
- PRENDES-GERO, M. B.; BELLO-GARCÍA, A.; COZ-DÍAZ, J. J.; SUÁREZ DOMÍNGUEZ, F. J.; GARCÍA NIETO, P. J. Optimization of steel structures with one genetic algorithm according to three international building codes. Revista de La Construccion, v. 17, n. 1, p. 47-59, 2018.
- RAMOS, J. R. S; ALVES, E. C. Dimensionamento otimizado de vigas mistas celulares utilizando algoritmos genéticos. In: SIMMEC - Simpósio de Mecânica Computacional, 13., 2018, Vitoria, ES. Anais […]. Vitória: ABMEC: UFES, 2018.
- SILVEIRA, E. G. Avaliação do comportamento de vigas alveolares de aço com ênfase nos modos de colapso por plastificação 2011. 156 f. Dissertação (Mestrado em Engenharia Civil) - Universidade Federal de Viçosa, Viçosa, MG, 2011.
- SONCK, D.; BELIS, J. Lateral-torsional buckling resistance of cellular beams. Journal of Constructional Steel Research, v. 105, p. 1199-128, 2015.
- SOUZA JUNIOR, D. A. Otimização pelo método dos algoritmos genéticos e dimensionamento de estruturas tubulares metálicas espaciais com barras cruzadas para coberturas 2005. 114 f. Tese (Doutorado em Engenharia Mecânica) - Faculdade de Engenharia Mecânica. Universidade Federal de Uberlândia, Uberlândia, 2005.
- VERÍSSIMO, G. S.; VIEIRA, W. B.; SILVEIRA, E. G.; RIBEIRO, J. C. L.; PAES, J. L. R.; BEZERRA, E. M.; CASTRO E SILVA, A. L. R.; FAKURY, R. H. Dimensionamento de vigas alveolares de aço. In: CONSTRUMETAL - Congresso Latinoamericano da Construção Metálica, 2012, São Paulo. Anais […]. São Paulo: ABCEM, 2012. 17 p.
Publication Dates
-
Publication in this collection
29 Mar 2021 -
Date of issue
Apr-Jun 2021
History
-
Received
11 Nov 2019 -
Accepted
17 Dec 2020