Evaluation of an iron ore price forecast using a geometric Brownian motion model

Abstract

Mining projects are often budgeted in millions of dollars, making it of interest to the investor to measure a project’s uncertainties and risks, which include the changes in the commodity price. The simulation of asset prices is valid because it enables displaying, with a degree of certainty, the future behavior of a financial asset. One of the most commonly used mathematical forecast models is the Geometric Brownian Motion (GBM) model. This article aims at simulating the forecast price of an iron ore commodity with the GBM method based on the historical price series and comparing it to other forecast approaches used in the financial market. The results of this study indicate that the model has limitations, which should be considered. However, it is an overall good tool to support the economic evaluation of a project, if performed along with other approaches.

Keywords:
commodity; mining projects; mathematical models; Geometric Brownian Model

1. Introduction

Investments in projects for the exploitation of mineral resources usually reach values of millions or even billions of dollars. In the decision-making process to invest or not in a project, the investor lacks not only return estimates, but also risk estimates, inherent for the dynamics of mineral commodity prices.

This creates a great interest in predicting how the commodity prices would evolve, as it would be advantageous for an investor to be able to predict the behavior of prices and thus reduce risks (Lima and Suslisk, 2006). In this sense, the simulation of asset prices is relevant to the assessment of project investments, being the use of mathematical models recurrent for simulating this parameter (Brandão, 2000).

In 1900, Louis Bachelier proposed one of the first models for price forecasting, which considered the evolution of the price of financial assets as a random process, similar to playing non-skewed dice. He suggested that the price (St) of a stock, at a given instant t≥ 0, would be a random variable that obeyed a certain probability distribution function (Volchan, 1999).

The physical phenomenon known as Brownian motion was first observed by the botanist Robert Brown, who noticed under a microscope that small pollen grains in aqueous solution have an incessant and irregular movement trajectory. Many proposals have been made to elucidate this phenomenon, until Einstein, in 1905, and Smoluchowsky, in 1906, managed to explain the phenomenon through probabilistic arguments, showing that this resulted from incessant random shocks of water molecules against the pollen grains. Bachelier’s proposition stated that stock prices behaved similar to the Brownian motion, i.e.: erratic and unpredictable (Duke, 2014).

Bachelier’s model, called Brownian Motion Arithmetic (BMA), received attention in the 60s, when some economists suspected that stock prices behave randomly due to the efficient market hypothesis according to which, at a given instant, the next price depends only on the price at that moment and not on its history of variations.

The economic understanding of this concept is that an efficient market reacts immediately to new information only, regardless of what happened in the past. Samuelson, in 1965, noted a limitation of the Bachelier’s model, as it could predict negative stock prices. This possibility undermines the principle of limited liability, which determines that a shareholder can lose, at maximum, the financial amount initially invested, so he cannot afford losses due to the poor performance of a company. The author also observed that the absolute value St was not as important as previously believed, but rather the so-called return (∆S/St), that is, the relative price change (Volchan, 1999).

Samuelson proposed the Geometric Brownian Motion (GBM) model, which associates the mathematical description of this physical phenomenon to the market efficiency hypothesis, generating a random process and respecting the limited liability principle (Neves, 2010).

This article aims at implementing and testing the Geometric Brownian Motion (GBM) using the historical iron ore commodity price series and comparing it to the predictions made by financial agents.

2. Material and method

To perform this investigation, a historical iron ore price series of the last 20 years (1997-2017) was obtained from the Index Mundi database <http://www.indexmundi.com>. This historical series was statistically treated to obtain the mean and standard deviation for the changes in the ore price over the 20 years period. After acquiring this data, the Wiener increment was tested to verify the randomness of the process, the geometric Brownian motion approach was implemented to predict the iron ore price for a time series, the demand and price forecasts for years to come were collected with experts, the simulation results were compared with iron ore price forecasts made by experts.

3. Results

3.1 Wiener process

Stochastic processes are understood as a collection of random variables (St, t ≥ 0) which evolve over the time, at least in part, randomly; that is, given an initial condition S₀, several possible paths for the evolution of collection are possible. The Brownian motion phenomenon (also named Wiener process) is a continuous time stochastic process which has three important properties (Pinkdyck and Dixit, 1993; Portal Action, 2018):

• It follows a Markov process, i.e.: the next moment’s estimate is made using only the current information, and it is not based on historical data;

• Its increments are independent, not reliant on changes in other time intervals;

• The increments follow a normal distribution (Ejarque, 2000).

The Wiener increment had its mathematical formulation presented using the Excel^® software. The command: INV.NORM.N was used, with "random" probability, mean value of "0" and standard deviation of "1".

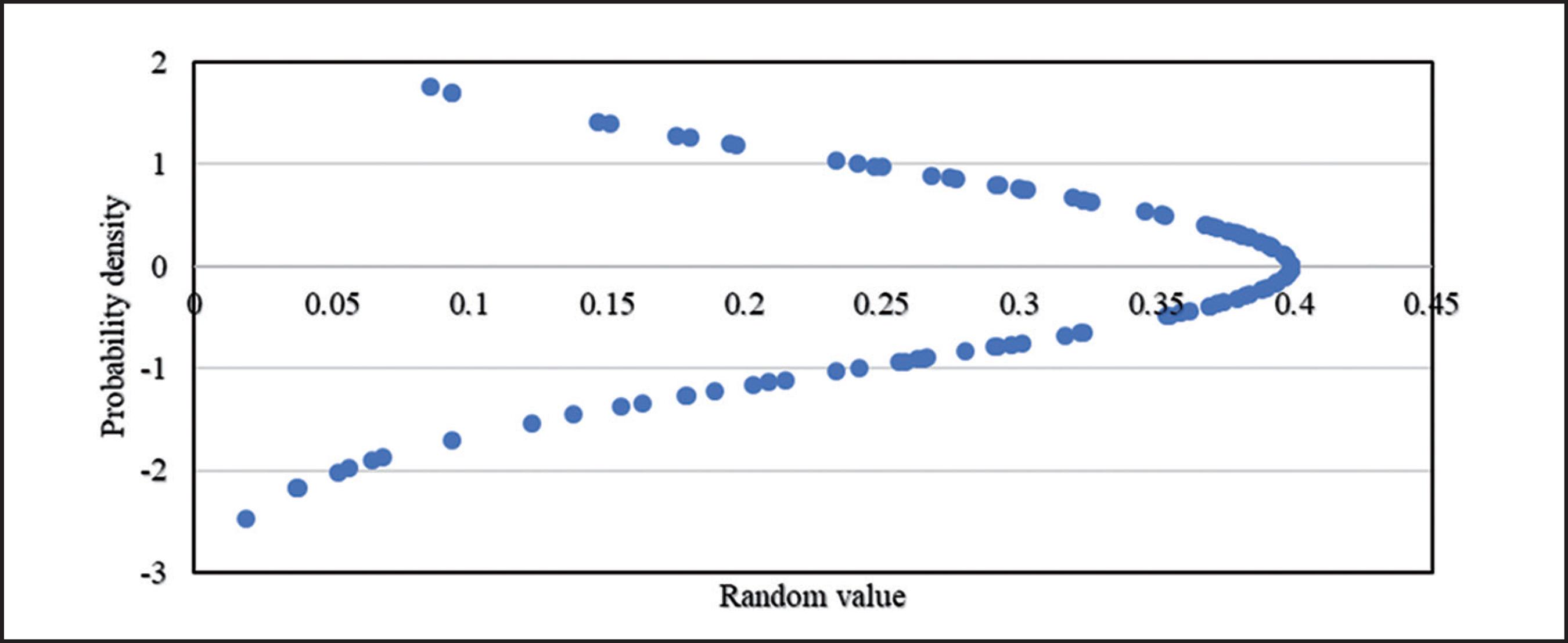
Figure 1 shows that the Wiener increment follows a stochastic process, i.e.: its evolution in time presents random character. As for their statistical properties (mean and standard deviation), the process can be classified as stationary when it holds these properties constant over time.

Figure 1
Random values as a function of time, generated using the command: INV.NORM.N.

Figure 2 shows that the increment generated over time follow a normal distribution ε ~ N (0, 1).

Figure 2
Normal Distribution of the values presented in Figure 1.

3.2 Geometric Brownian motion (GBM)

The proposed mathematical model considers that a temporal evolution of prices is a solution for a stochastic differential equation as shown in Equation 1 (Goodman, 2012).

(1) $\frac{\mathit{dSt}}{\mathit{St}}=\mu \mathit{dt}+\sigma \mathit{dWt}$

Where dSt/St = return (relative price change), µdt = assets’ growth rate, σ = volatility, and Wt = Wiener increment.

Volatility (σ) is defined, in the financial market, based on supply and demand. Commodities are transnational products and are traded on commodity exchanges, usually having long historical series. In this case, the future volatility is obtained through the historical volatility of the commodity, based on the standard deviation of the time series (Lima and Suslick 2006), according to Equation 2.

(2) $\sigma =\sqrt{\frac{1}{n-1}\Sigma {\left(\mathit{St}-\dot{\mathit{S}}\right)}^2}$

The growth rate of the asset (µdt) describes the time evolution (dt) of an investment that continually yields at a constant interest rate (µ), which can be represented by the average of a particular historical series or determined based on other factors (Brandão, 2000).

Equation 1 is expressed by Equation 3, which gives St for a continuous time interval.

Where St = share value at time t; S₀ = previous share value; µdt = asset’s growth rate; s = volatility; Wt = Wiener increment.

(3) $\mathit{St}={\mathit{S}}_{\mathit{0}}·\mathit{e}\left[\left(\mu -\frac{{\sigma }^2}{2}\right)·t\right]+\sigma \mathit{Wt}$

As the random character of the GBM model stands out in the short term, this approach presents the limitation of not allowing the investigation of any behavior trend. In the long run, however, this is not observed, and a trend can be studied. Figures 3 and 4 illustrate both scenarios by presenting the most random character in the short term (6 months) and a trend in the long term (6 years), for the same simulation.

Figure 3
Commodity price simulation for a short-term period (6 months).

Figure 4
Commodity price simulation for a long-term period (6 years).

Another restriction of the GBM model is that it can diverge if the time series is built for long-term period, driving the price (St) to infinity; in that sense some simulations that follow the model may not be realistic. Figure 5 shows an example of this restriction, presenting a simulation of prices for the next 50 years where they reach up to over US$ 40,000.00.

Figure 5
Iron ore price forecast for next 50 years.

3.3 Market demand expectations

Demand is defined as the amount of goods and services that can be bought at a particular price. Demand forecasts may be carried out through qualitative and quantitative methods (Sharma and Sharma, 2015).

In 2015, the World Economic Forum reported the three most relevant scenarios for the world development by 2050. These scenarios are not predictions, but can point to important demand issues, which stakeholders (mining and steelmaking companies) need to be aware of to enable strategic planning. Named “world in two speeds”, the first scenario is characterized by the appearance of two or more possible groups of countries. One group, "the sustainable forerunners", is rapidly advancing to the sustainable use of commodities and metals, while the other group, "the mineral dependents" is concerned with ensuring growth and jobs through traditional mining. In this group, the recycling sector is less developed, and the environmental impacts can be mitigated by the technological advance.

The second scenario, in which there is no shortage of raw materials, is named "resource abundancy". This might come to be due to technological advances, discovery of new ore deposits and innovation in the use of the currently available resources. This scenario may be feasible with mining in new areas such as the seafloor and asteroids. As the economy moves towards open markets and global business, additional consumption can arise in regions all over the world. This could result in an increase in the extraction of mineral resources, raising waste production and intensifying environmental issues.

In the third scenario, named "global fragmentation", an increase in the competition for resources among countries is expected, due to the inability to reconcile supply and demand. Resources, including minerals, water, food among others are depleted faster than expected or not negotiated properly, whereby the demand for these commodities cannot be met. Countries create export quotas for these resources to meet their domestic demand and, in some cases, this protectionism leads to international conflicts. In this scenario, characterized by conflicting national interests, there is a political and economic fragmentation at the global scale.

Regardless of the possible scenarios, conclusions can be drawn for the industry: mining should not disappear, extraction should continue, but the volumes are unlikely to grow aligned with the world’s gross domestic product (GDP). This could mean that pressure for efficient cost and effect of the scale will remain for the foreseeable future. Demand for cost efficiency will exist in parallel with the demand for responsible environmental and social actions. Regulations change, social pressure to act more sustainably grows and the increasing use of circular commodities and metals show a potential to disrupt the industry. In the face of these expected global changes, mining companies need to identify the actions needed to be taken today, aiming to better prepare to be industrial leaders in the future (World Economic Forum, 2015).

For the year 2018, Vale, the largest iron ore mining company operating in Brazil, expects moderate economic growth in China, with some downside risks. In contrast, the inventory levels and investments should only see a small decrease. Globally, the economic outlook remains positive, as it is expected a world’s GDP growth from 3.6% to 3.9%, according to the International Monetary Fund (IMF). The steel demand and production should increase with the emergence of new projects in Southeast Asia, a region with a deficit in steel production and lowest consumption of steel per capita. Vale expects its 2018 iron ore production to be at around 390 million tons (Vale S.A, 2017).

Based upon these perspectives, since the first quarter of 2017 (1T17), Vale is reducing its low-grade ore production and positioning itself as a premium ore producer as a result of a rigid production and sales discipline to achieve maximum margin over volume. In line with its strategy, in the first semester of 2018 (1T18), Vale reached a record in the volume of iron ore and pellets (84.3 Mt) sold in a first quarter; 6.4 Mt higher than in 1T17. The company sales portfolio improved substantially year after year due to the ramp-up of the S11D project and the decision to reduce the production of low-grade ore. The company’s sales portfolio boosted the upward impact of the market premium, leading to an increase in the quality and premium average price which equaled US $ 5.2/t in 1T18 whereas it achieved US$ 2,3/t in 1T17, and US$ 3,9/t in 4T17.

The iron ore production in 1T18 reached 82.0 Mt, 4.2 Mt and 11.4 Mt below the production achieved in 1T17 and 4T17, respectively, mainly due to the decision made in 2017, to reduce the production of low-quality ore (Vale S.A., 2018).

3.4 Price forecasts by experts

Citigroup expects that the iron ore price (62% Fe) should reach US $ 60-62/t, by the second semester of 2018, which could persist throughout 2019. This was an update in the forecast due to a more positive evaluation of China`s steel demand and the global consumption of high-content iron ore. Simultaneously, the commodity supply struggles to meet these expectations due to lack of investment in recent years and because long-term periods are required for the expansion of the production capacity (Citigroup, 2018).

Goldman Sachs predicts that iron ore prices should drop to US$ 60/t in the first quarter of 2018, US$ 55/t in the first half of the year and even drop to US$ 50/t at the end of 2018. The company believes that to ramp-up of Vale`s project, S11D, could increase the iron ore supply, whereas China's demand should decrease.

In October 2017, HSBC noted a weaker iron ore demand trend which could lead to a surplus of about 40 million tons of ore, and a consequent price reduction to values below US$ 60/t in the first half of 2018 (Market Realist, 2018).

The World Bank Group predicts iron ore prices of US$ 57/t, US$ 50/t, and US$ 50.8/t for the years 2018, 2019 and 2020, respectively (World Bank Group, 2017).

In contrast, Credit Suisse has a more positive outlook for iron ore prices in the years 2018, 2019 and 2020. The major reasons for this are: greater profitability of the Chinese steel industry; greater supply control from the four largest iron ore producers; the belief that the supply would decrease rapidly if prices go under $ 60/t; and China's demand supported by infrastructure investments of approximately 20% per year (Market Realist, 2018).

4. Results and discussion

The iron ore price forecast (62%, c.f.r) using the GBM model was based on a 20-year price series for the commodity (1997-2017), taken from the Index Mundi database <http://www.indexmundi.com>. The growth rate (µ) was generated based on the average of this historical price series, leading to µ = 1.10092% monthly. The term volatility (σ) assumed σ = 8.97577% per month based on the standard deviation of the same set of historical prices.

Considering the experts’ demand and price forecasts, the inability to predict the future behavior of shares and the fact that a single simulation is not representative to evaluate future trends, the Monte Carlo simulation (MCS) was used to determine a minimum number of simulations to establish a likelihood of a value to occur. The MCS approach consists in randomly generating N successive samples (commodity price) which will be tested along with a probability distribution function of the variable being investigated. The minimum number of iterations (N) is given by Equation 4.

(4) $\mathit{N}={\left(\frac{3\sigma }{\epsilon }\right)}^2$

Where σ is the standard deviation between minimum, maximum and their average and ε is the absolute error or mean between minimum and maximum value multiplied by the relative error (Fernandes, 2005).

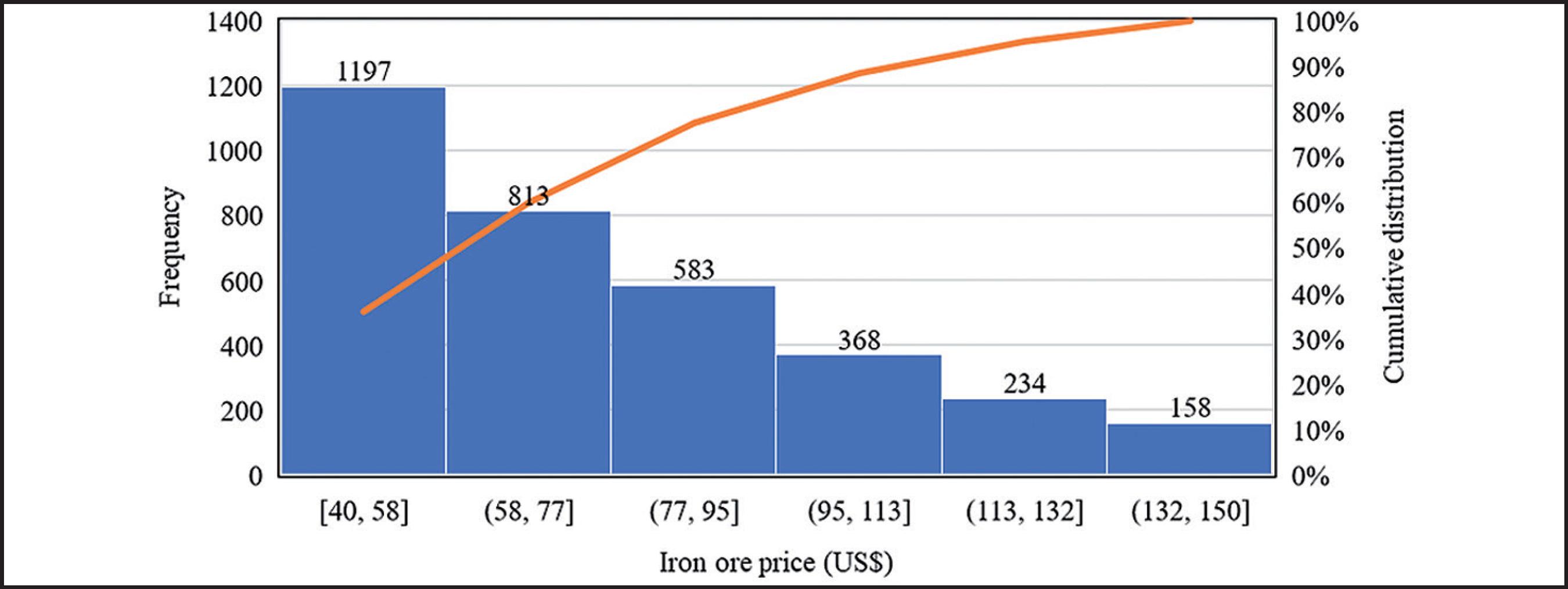
For this study, the minimum number of simulations (N) was set 2235 to guarantee a relative error of 3 %, a minimum price value was set US$ 40.00/t, and the maximum value was set US$ 150.00/t. The number of simulations conducted was set as 5760, which is 2.5 times the minimum number of simulations. Figure 6 shows the set of simulations for the forecast. Only part of the simulations is shown in this figure due to computational limitations.

Figure 6
Multiple simulated scenarios for a 5-year time series.

The World Bank iron ore price forecast, for the same simulated time series, is US$ 50.8/t. If only the simulated values between the minimum (US$ 40/t) and maximum (US$ 150/t) are considered from the MCS, 3226 simulations are obtained. Considering the cumulative distribution histogram in Figure 7, it is possible to infer that there is an 80% probability that the price will be less than US$ 120/t. There is also a 18.4% probability that the value will fall within the US$ 40/t - US$ 60/t range, comprising the US$ 50.8/t prediction from the World Bank.

Figure 7
MCS with 3226 simulations.

The 57.6% percentage difference between the highest simulated value (US$ 120/t), with 80% cumulative probability, and the value predicted by the World Bank (US$ 50.8/t) may be due to the use of a different time series, a different mathematical model or even the determination of the growth rate and volatility values from other parameters, i.e.: political and economic. Considering the previous paragraph’s discussions, a new round of simulations was generated based on the same historical series, although a new interval (April 2010 to January 2017) was chosen. This range was chosen because it marks a historical shift in the iron ore pricing approach. Before this period, the iron ore prices were governed by annual contracts between mining and steel companies and, after, prices were defined at the spot market (spot).

Using this time series interval, a new growth rate and volatility were generated (µ = - 0.27146%, s = 9.03786%). For the same time series of 5 years and the same number of simulations (5760), only the values between the minimum (US$ 40/t) and maximum (US$ 150/t) were selected as parameters of the MCS, leading to 3353 simulations. Considering the results in Figure 8, it can infer an 80% probability that the iron ore price will be less than US$ 100/t and a 38.3% probability that the value will fall within the range (US$ 40/t - US$ 60/t), which includes the forecast of US$ 50.8/t from the World Bank.

Figure 8
MCS with 3353 simulations.

This second simulation is closer to the forecasts made by financial market specialists and shows the ability to use different criteria to determine the growth rate and volatility parameters for the GBM approach.

5. Conclusions

These results indicate that the GBM model can be used to estimate commodity prices when considering information on ore reserves, market, political context among others. The method is a good tool to aid in reducing investment risks and uncertainties, whereas the routine described herein can be easily implemented in spreadsheets. The model, like any other, has limitations, especially to predict short term trends, and should be used in conjunction with other quantitative and qualitative models.

References

• BRANDÃO, L. Processo de Ito. In: Dixit and Pindyck Rio de Janeiro: PUC-Rio. 2000.
• CITIGROUP. 2018 annual outlook New York: 2018. p. 14.
• DIXIT, A. K., PINKDYCK, R. S. Investment under uncertainty New Jersey: Princeton university press, 1994.
• DUQUE, O. M. L. Uma breve análise do movimento browniano Vitória: Universidade Federal do Espírito Santo. 2014. p. 50-51.
• EJARQUE, J. Investment theory handout 2 University of Copenhagen: 2000. p. 1.
• FERNANDES, C. A. B. D. A. Gereciamento de riscos em projetos: como usar o microsoft excel para realizar a simualação monte carlo (S,l): Cinq Technnologies Ltda. 2005. p. 3.
• GOODMAN, J. Stochastic differential equations New York: New York University. 2012. p. 1.
• LIMA, G. A. C, SUSLISK, S. B. Estimativa da volatilidade de projetos de bens minerais. Rem: Revista Escola de Minas, v. 59, n. 1, p. 37-46, 2006.
• MARKET REALIST. What are analysts predicting for iron ore prices in 2018? Market realist, 2018. Available: <https://marketrealist.com/2018/01/analysts-predicting-iron-ore-prices-2018>. Accessed: April 2018.
  » https://marketrealist.com/2018/01/analysts-predicting-iron-ore-prices-2018
• NEVES, C. D. Geração de preços de ativos financeiros e sua utilização pelo modelo de black and scholes . In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, 30. Sao Carlos: Associação Brasileira de Engenharia de Produção, 2010. p. 1-2.
• PORTAL ACTION. Movimento Browniano. Portal action, 2018. Available: <http://www.portalaction.com.br/processo-estocastico/movimento-browniano>. Acessed: April 2018.
  » http://www.portalaction.com.br/processo-estocastico/movimento-browniano
• SHARMA, S. K., SHARMA, G. K. Demand forecasting techniques vis-a-vis demand for lead. Procedia earth and planetary science, Nagpur , p. 418-424, 2015.
• VALE S.A. Relatório Anual 2017 Rio de Janeiro: 2017. p. 86.
• VALE S.A. Produção e vendas da Vale no 1T18 Rio de Janeiro: 2018. p. 3-4.
• VOLCHAN, S. B. Modelos matemáticos em finanças: avaliação de opções Rio de Janeiro: Matemática Universitária, 1999. p. 67-121.
• WOLRD BANK GROUP. 2017 commodity markets outlook. Washington, DC: 2017. p. 14.
• WORLD ECONOMIC FORUM. Mining and metals in a sustainable world 2050. [Sl]: World economic forum, 2015.

Publication Dates

• Publication in this collection
  Jan-Mar 2019

History

• Received
  03 Sept 2018
• Accepted
  26 Oct 2018