Abstract
Non-linear geostatistical methods are known to deal appropriately with the geological and geometrical complexity of gold deposits. This article reports the results related to an investigation to improve the gold content estimate based on restricted ore modeling to honor the structural aspects that control the mineralization. The grade domains are defined by using structural measurements to guide the indicator kriging (IK) estimator. Relevant grade intervals are chosen as indicators. Kriging the indicators provides a measure of the grade uncertainty at the sample support. The probability indicator modeling relies on thresholding the estimates which are represented by cumulative distribution functions (cdf) at the unsampled locations. The implicit concept of probability means that the chance of an estimated node belonging to a given grade domain is as big as the estimated IK value. The geological consistency of IK models requires a proper definition of some key parameters: The probability thresholds and indicator variogram models must honor the structural features and stationarity conditions of grade intervals. The geological representativeness of these models depends heavily on thresholding the estimates. For instance, extremely permissive estimates may produce overrepresented ore domains. The decision of the optimal indicator probability for defining the ore boundaries is made by iterative comparison. Several thresholds were applied to kriged maps and the results reconciled to the most sampled areas until achieving reasonable geological adherence. The mineralization continuity often varies according to local structural features and so dynamic anisotropy is used to control the variogram direction and search ellipse to consider the significant scale trend and small-scale fold geometries. A case study based on a real gold deposit dataset was performed and the method was discussed. The IK models can define precisely the mineralization bounds in the most detailed areas. However, the results presented some limitations on reproducing the geological expectation in regions of wide drilling spacing. The lack of information in some areas led to an excessive number of small sub-zones. The method allows a faster and efficient modeling of structurally complex geometries and provides an uncertainty assessment which may be useful to support exploratory and short-term decisions.
Keywords:
structural geology; geological modelling; Indicator Kriging; geostatistics
1. Introduction
The resource evaluation of deposit is composed of two steps: definition of the boundaries of tthe various geological domains and estimation or simulation of grades for each unit. (Chilès et al., 2004CHILÈS, J et al. Modelling the geometry of geological units and its uncertainty in 3D from structural data: the potential-field method. In: INTERNATIONAL SYMPOSIUM ON OREBODY MODELLING AND STRATEGIC MINE PLANNING, 2004, Perth, Australia. Proceedings […]. [S. l.]: AusIMM, p. 24.)
In mining, 3D ore models are routinely supported by computational tools, being that the general workflow: (i) ore/waste contour lines are interpreted based on cross sections; (ii) the outlined contacts are then linked to each other to create three-dimensional solids (Abzalov, 2016ABZALOV, M. Z. Applied Mining Geology. Switzerland: Springer International Publishing, 2016. p. 195. (Modern Approaches in Earth Sciences 12).). Specially for complex geometries, such as strongly deformed mineralization. The traditional modelling may be a cumbersome task and sometimes based on subjective criteria of interpretation.
Implicit modelling algorithms provide an alternative solution replacing the handwork digitization by automatized procedures (Silva, 2015). Common implicit algorithms interpolate distance functions between categorized samples. The bounding interface of interest is the surface corresponding to specific iso-values of estimated distance functions (Rollo, 2017). Implicit functions are interpolated by implementing a method known as radial basis function (RBF). While kriging uses covariance calculated from data, RBF interpolator instead, uses pre-defined interpolant functions (e.g. spheroidal, linear) to improve the processing time. Despite the singularities of how data are weighted, both RBF interpolants and indicator models are based on kriging mathematical formulation.
Different application of indicator modelling can be found in geoscience. Abzalov (2003ABZALOV, M. Z.; HUMPHREYS, M. Resource estimation of structurally complex and discontinuous mineralization using non-linear geostatistics: case study of a mesothermal gold deposit in northern Canada. Exploration and Mining Geology, Canada, v. 11, p 1-4, 2003.) and Oliveira (2011OLIVEIRA, S. B. Indicator Kriging applied to lithotypes of the Ni-Cu deposit located in Americano do Brasil, GO. Revista do Instituto de Geociências, São Paulo, v. 11, n. 2, p. 123-134, 2011.) discussed IK domaining of mineral deposits. The concept has also been employed for modelling facies of sedimentary deposits (Deutsch, 2002DEUTSCH, C. V. Geostatistical reservoir modeling. New York: Oxford University Press, 2002. 376 p.) and creation of probabilistic maps of risk (Landim and Sturaro, 2002LANDIM, P. M. B.; STURARO, J. R. Krigagem indicativa aplicada à elaboração de mapas probabilísticos de riscos. Rio Claro: IGCE/UNESP, 2002. (Geomatemática,Texto Didático 6).).
The indicator modelling supported by dynamic anisotropy was tested on data of an orogenic lode gold deposit located in the Quadrilátero Ferrífero (MG, Brazil) metallogenetic district.
2. Geological background
The present investigation is applied to a gold deposit hosted in the Rio das Velhas Supergroup units, situated in the eastern Quadrilátero Ferríferro district (QF) (Brazil). The Archean Rio das Velhas is a greenstone belt known for hosting various gold occurrences, including world-class deposits (Lobato, 1998LOBATO, L. M.; VIEIRA, F. W. R. Styles of hydrotermal alteration and gold mineralization associated with the Nova Lima Group of the Quadrilátero Ferrífero: part II, the archean mesothermal gold-bearing hydrothermal system. Revista Brasileira de Geociências, v. 28, n. 3, p. 335-336, 1998.).
Based on the host rock and mineral assemblage, Vieira (1987VIEIRA, F. W. R Gênese das mineralizações auríferas da mina de Raposos. In: SIMPÓSIO DE GEOLOGIA DE MINAS GERAIS, 4., 1987, Belo Horizonte Anais […]. Belo Horizonte: SBG, 1987. v.7, p. 358-368.) distinguished three main gold mineralization types in the QF: (i) rich-pyrrhotite hosted in banded iron formation; (ii) related to pyrite and arsenopyrite replacing the iron layers of banded formations; and (iii) disseminated arsenopyrites in mafic schists. The case study refers to a type (iii) mineralization with pronounced structural control.
The folds that control the gold mineralization have their axes plunging to NE parallel to the main ore shoots. The smoky quartz veins usually representing the primary type of mineralization, are either folded or elongated in boudins (Roncato et al. 2015RONCATO, J. G; LOBATO, L. M; LIMA, C. L; PORTO, C. G; FIGUEIREDO, R. C. Metaturbidite-hosted gold deposits, Córrego do Sítio lineament, Quadrilátero Ferrífero, Brazil. Brazilian Journal of Geology, v. 45, n.1, p. 5-22, Mar. 2015.) . Based on the geological mapping survey carried out in the deposit, Afonseca (2020AFONSECA, B. C. D. Geoestística não-linear aplicada à modelagem e estimativa de recursos recuperáveis em mineralização aurífera estruturalmente complexa. 2020. Dissertação (Mestrado) - Escola de Engenharia, Programa de Pós Graduação em Engenharia de Minas, Materiais e Metalurgia, Universidade Federal do Rio Grade do Sul, Porto Alegre, 2020. p. 71-73. In press.) discusses a concept of strain partitioning of the deformational process observed at the open pit scale. The deformation is partitioned along the ore strike, where the high strain domain is represented by complete transposition of the host rock bedding. The low strain domains appear as close to tight fold geometries. The presented 3D modeling methodology aims to efficiently reproduce these structurally distinct domains.
3. Methodology overview
The modelling methodology combines dynamic anisotropy, probability indicator models and post-processing step based on iso-surfacing to define a geological grade model.
3.1 Dynamic anisotropy
Grade estimation processes traditionally employ a global oriented search volume to select samples used for interpolation. The ellipsoid representing the anisotropy of the estimated property is centred on each node to be estimated. Once a grid node is estimated, the search volume moves to the next node, until the full grid is passed by. However, the grade’s continuity often varies with direction, such as in deformed deposits and ignoring this feature leads to unrealistic results. One solution is to create sub-domains related to different structural sectors. This approach has some drawbacks: Sub-domaining may be time consuming since individual assessment about the ore geometries, variogram models, and data analysis must be undertaken. Additionally, the reduction of data amount can impact the quality of the evaluation.
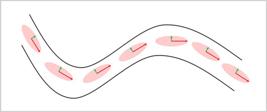
The dynamic anisotropy solution allows the orientation of the ellipsoid and variograms to be defined individually for each node to be estimated. The method improves the estimation process as the search volume are defined according to the local continuity of mineralization (Figure 1). The implementation of dynamic anisotropy requires that all points to be estimated are assigned with rotation angles corresponding to the local anisotropy (Datamine, 2019DATAMINE. Studio RM Technical References. [S. l.]: Datamine, 2019.).
Example of how dynamic anisotropy works on the search volume orientation according to the ore continuity.
3.2 Indicator kriging
Non-linear methods, such as indicator kringing (IK) presented by Journel (1983JOURNEL, A. G. Non-parametric estimation of spatial distributions. Journal of International Association for Mathematical Geology, v. 15, n. 3, p. 445-468, 1983.), works on non-linear transformed data. Differently from ordinary or simple kriging, the IK employs the concept of cumulative distribution functions (cdf) to predict spatial distributions. These types of estimators are not specifically committed to estimate a given property. Instead, the fundamental purpose of IK is to provide a local estimate of the probability distribution, quantifying the uncertainty through a histogram (Journel, 1983JOURNEL, A. G. Non-parametric estimation of spatial distributions. Journal of International Association for Mathematical Geology, v. 15, n. 3, p. 445-468, 1983.). Each estimated point will have an individual cdf.
IK formalism consists in converting data into indicators according to the methodology established by Journel (1983JOURNEL, A. G. Non-parametric estimation of spatial distributions. Journal of International Association for Mathematical Geology, v. 15, n. 3, p. 445-468, 1983.). The indicator I(u,zc) at u position for a zc cutoff is a binary variable assuming values according to the following conditions:
The indicator random variable I(u,zc) has only two possible outcomes, 1 or 0. Thus, by definition, the expected value can be obtained through an equal-weighted average (Rossi and Deutsch, 2013):
For a given interval Z, the indicator is referred as a random function of u. Therefore, the IK consists in estimating I by kriging the random function I(u,zc) (Chilès and Delfiner, 1999). The practical consequence is that a conditional cdf can be built by assembling the indicator estimates. This cdf represent a probabilistic model for the uncertainty about unsampled values which can be obtained with a weighted linear average. The optimal weights λ are obtained by kriging system on the indicator data (Rossi and Deutsch, 2013):
Basically, IK consists in applying the ordinary kriging on transformed data. An advantage of IK relies on being a non-parametric method. It does not make any prior assumption about the distribution being estimated. This allows prediction of distribution functions of variables with wide spatial variability (Rocha and Yamamoto, 2003ROCHA, M. M.; YAMAMOTO, J. K. Simulação direta de teores e estimativa de litologias na mina de ouro de São Vicente. São Paulo: FAPESP, 2003. (Rel. Interno.).; Rossi and Deutsch, 2013).
The concept behind using indicator estimates for defining geological domains relies on thresholding the probabilities informed by kriged cdf’s at unknown locations. The implicit concept of probability means that the chance of an estimated node belongs to a given grade domain is as big as the IK estimate result.
3.3 Post-processing
In practice, geology routines demand three-dimensional solids instead spatial probabilities. Hence the cloud of points provided by the indicator model should be combined in such a way so as to produce uniform geometries becoming manageable for the short-term activities.
The contouring of estimates can be achieved through iso-value interpolation. The interpolation is processed by connecting estimated values according to pre-defined acceptance criteria. The decision of the indicator probability value that is optimal for defining the ore boundaries was made by iteration. Several thresholds were applied to kriged maps and the results reconciliated to the most sampled areas until achieving reasonable geological adherence.
4. Application
4.1 Database
The database used is composed of exploratory, infill drilling and channels samples (Figure 2). obtained by different sampling techniques, such as diamond drilling, reverse circulation and mechanical auger drilling.
Sampling location maps. Left the exploratory drillholes lines, on the right grade control channels.
To assure equal volume support, the data were composited at 1m prior to estimate. A total of 130,394 composites have been transformed to indicators using the methodology proposed by Journel (1983JOURNEL, A. G. Non-parametric estimation of spatial distributions. Journal of International Association for Mathematical Geology, v. 15, n. 3, p. 445-468, 1983.). Table 1 presents the Au statistics for each sampling type.
Operational inputs and geological understanding of the deposit support the decision of using 0.8 g/t as a threshold for defining the high-grade mineralization. The chosen value enables subdivision of the mineralized portion from the marginal grade portion. The spatial continuity at the 0.8 g/t indicator was modelled and pseudo-probabilities estimated by ordinary kriging.
4.2 Anisotropy and variograms
The mineralization displays strong structural control along shear corridors nearly oriented NNE. The indicator variogram map tested four horizontal directions (N18, N54, N108, N153) and it clearly reproduced the expected mineralisation structural control. Continuity is maximum on strike direction (NE) and gradually decreases towards SE azimuth which represents the orebody thickness. (Figure 3).
Variographic map (left) produced on horizontal plan highlighting the continuity along NE direction. Experimental variograms (right) from the map.
Figure 4 presents the indicator variogram models. Mineralization continuity is given by the geometry of the major structures. The greatest continuity (plunge) coincides with the folding axis. Semi-major direction is sub-parallel to the limbs´ dip and minor direction represents the veins´ width. The rotation convention adopted to define the anisotropy is 27º/48º/34º around vertical, X and Y axis respectively.
The resulting parameters derived from modeled variograms are presented in Table 2.
Continuity of mineralization often varies according to local structural features and so dynamic anisotropy was used to impose variogram direction and search ellipse to consider the major scale trend and small-scale fold geometries. A robust database of structural measurements assisted on creating the structural outlines (Figure 5).
Points of structural measurements from geological mapping (a), stereogram plot of folds related foliation (b).
Stereogram of the axial planes (Figure 5a) indicates fluctuation of the structural controls along the deposit. In order to honour the local geometries, mapping data was used on interpretation of the major structural trends (Figure 6a). Geological surfaces were created three-dimensionally and represent local folding (Figure 6b). Finally, several points containing specific information of the structural attitudes were extracted from the 3D modeled surfaces (Figure 6c). Dynamic anisotropy considered the attitude points derived from structural contours to guide the indicator kringing neighborhood.
Structural interpretation from geological mapping (a), modeled structural surfaces (b), attitude points extracted from the surfaces used to guide dynamic anisotropy (c). Perpendicular view to ore plunge.
4.3 Indicator model
An important input that directly affects the quality of geological adherence of probability indicator models is the estimation grid. The grid spacing and orientation should be capable of reproducing the geometrical features of the estimated variable.
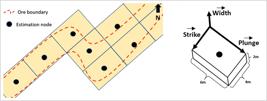
The channel sampling is preferably taken orthogonally to the mineralized structures; hence, it provides the best approximation of orebody thickness. The average thickness from channel composites was used as the shortest grid spacing. Additionally, rotation was processed to guarantee a better representation of the overall anisotropy (Figure 7).
Scheme of rotated estimation grid showing better adherence to the ore continuity (left). Grid dimension and orientation along anisotropy directions (right).
IK was constrained to an octant-based data search requiring at least 4 filled octants. The grid estimate was run using the search parameters informed in Table 3. A sectorized ellipse and sample restriction were required to prevent the occurrence of negative wheights and excessive estimates based on unique drillholes.
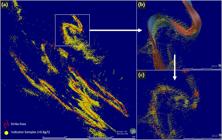
Major structural features were visually reproduced on different areas of the deposit. The cross sections of Figure 8 are representative of two different structural domains. The following probability maps enabled the calibration of the indicator acceptance level due to dense data availability.
Indicator probability maps on two representative sections of the deposit. The cross-section 1 presents a higher strain level compared to cross-section 2.
4.4 Post-processing (Tolerance level and points contouring)
Geological representativeness of probability indicator models depends heavily on thresholding the estimates. Inappropriate thresholding may produce unrealistic results. For instance, extremely permissive estimates may overrepresent ore domains. Otherwise too restrictive limits will mask the geological continuity by isolating clusters of estimated points.
Abzalov and Humphreys (2003ABZALOV, M. Z.; HUMPHREYS, M. Resource estimation of structurally complex and discontinuous mineralization using non-linear geostatistics: case study of a mesothermal gold deposit in northern Canada. Exploration and Mining Geology, Canada, v. 11, p 1-4, 2003.) suggested that the optimal ranges for probabilities can be selected from the detailed studied areas by comparing the indicator probability map with the corresponding geological interpretation and database. The decision of the indicator probability value that is optimal for defining the ore boundaries was made by iteration. Several thresholds were applied to kriged maps and the results reconciliated to the most sampled areas until achieving reasonable geological adherence. Increasing threshold values were applied and the map compared to the drilling data (Figures 9-10).
Reconciliation between the indicator composites and truncated estimate values was assessed. The level of 0.4 for probability was chosen as threshold for domaining. The chosen value enabled good adherence to the geological expectations in both cross-sections.
Finally, the estimates were merged into a 3D surface (Figure 11). Mining software packages provide different tools for wireframing. This study applied a simple iso-surface algorithm for contouring the points. The interpolation was processed by connecting estimated values at defined probability limit. The iso-value model was also reconciliated to the drilling data and IK estimates.
Reconciliation of the 0.4 iso-value surface with data and IK estimates. Morphology of boudins and ore discontinuities were well preserved.
Results demonstrate that even complex geometries were well represented by the indicator model. The value of 0.4 produced plausible outlines without an excessive number of sub-zones or overly broad lateral extents. Natural morphology of boudins and mineralization discontinuities were preserved by the iso-value model (Figure 11). The quality of geological adherence is higher as the number of structural measurements and indicator composites available. Areas with a lower level of information resulted in scattered volumes and progressive loss of natural continuity of mineralization. However, even not fully capturing the geological continuity along sparse drilling areas, the method provided a conceptual interpretation for supporting early stages of modeling.
5. Conclusions
The presented methodology proved to be effective on reproducing the geological features of discontinuous and structural complex deposits. Probability models were able to precisely define the mineralization bounds at the most well-sampled areas. However, the results in areas of wide drilling spacing are limited. Estimates from an insufficient amount of information masked the natural continuity by individualizing the deposit in small sub-zones. Specially in strongly deformed deposits, structural geology inputs, such as field measurements, provide valuable information for modeling. The dynamic anisotropy significatively improved the quality of predicting the folded geometries.
Although not replacing experienced geomodelers, the indicator probability approach shows some advantages over conventional techniques. The method allows a faster and efficient modeling of structurally complex geometries, as well as providing an uncertainty assessment which may be useful to support exploratory and short-term decisions.
References
- ABZALOV, M. Z.; HUMPHREYS, M. Resource estimation of structurally complex and discontinuous mineralization using non-linear geostatistics: case study of a mesothermal gold deposit in northern Canada. Exploration and Mining Geology, Canada, v. 11, p 1-4, 2003.
- ABZALOV, M. Z. Applied Mining Geology Switzerland: Springer International Publishing, 2016. p. 195. (Modern Approaches in Earth Sciences 12).
- AFONSECA, B. C. D. Geoestística não-linear aplicada à modelagem e estimativa de recursos recuperáveis em mineralização aurífera estruturalmente complexa 2020. Dissertação (Mestrado) - Escola de Engenharia, Programa de Pós Graduação em Engenharia de Minas, Materiais e Metalurgia, Universidade Federal do Rio Grade do Sul, Porto Alegre, 2020. p. 71-73. In press.
- CHILÈS, J et al Modelling the geometry of geological units and its uncertainty in 3D from structural data: the potential-field method. In: INTERNATIONAL SYMPOSIUM ON OREBODY MODELLING AND STRATEGIC MINE PLANNING, 2004, Perth, Australia. Proceedings […]. [S. l.]: AusIMM, p. 24.
- DATAMINE. Studio RM Technical References [S. l.]: Datamine, 2019.
- DEUTSCH, C. V. Geostatistical reservoir modeling New York: Oxford University Press, 2002. 376 p.
- JOURNEL, A. G. Non-parametric estimation of spatial distributions. Journal of International Association for Mathematical Geology, v. 15, n. 3, p. 445-468, 1983.
- LANDIM, P. M. B.; STURARO, J. R. Krigagem indicativa aplicada à elaboração de mapas probabilísticos de riscos Rio Claro: IGCE/UNESP, 2002. (Geomatemática,Texto Didático 6).
- LOBATO, L. M.; VIEIRA, F. W. R. Styles of hydrotermal alteration and gold mineralization associated with the Nova Lima Group of the Quadrilátero Ferrífero: part II, the archean mesothermal gold-bearing hydrothermal system. Revista Brasileira de Geociências, v. 28, n. 3, p. 335-336, 1998.
- MAUREIRA, D. A. S. Enhanced geologic modeling with data-driven training images for improved resources and recoverable reserves 2015. Thesis (Doctor in Mining Engineering) - Faculty of Engineering, University of Alberta, Edmonton, 2015.
- OLIVEIRA, S. B. Indicator Kriging applied to lithotypes of the Ni-Cu deposit located in Americano do Brasil, GO. Revista do Instituto de Geociências, São Paulo, v. 11, n. 2, p. 123-134, 2011.
- ROCHA, M. M.; YAMAMOTO, J. K. Simulação direta de teores e estimativa de litologias na mina de ouro de São Vicente São Paulo: FAPESP, 2003. (Rel. Interno.).
- ROLO, R. M. Modelagem geológica implícita com funções de distância assinaladas 2017. 106 f. Dissertação (Mestrado em Engenharia) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2017.
- ROLO, R. M; RADTKE, R; COSTA, J. F. C. L. Signed distance function implicit geologic modeling. REM - International Engineering Journal, Ouro Preto, v. 70, n. 2, p. 221-229, June 2017.
- RONCATO, J. G; LOBATO, L. M; LIMA, C. L; PORTO, C. G; FIGUEIREDO, R. C. Metaturbidite-hosted gold deposits, Córrego do Sítio lineament, Quadrilátero Ferrífero, Brazil. Brazilian Journal of Geology, v. 45, n.1, p. 5-22, Mar. 2015.
- ROSSI, M. E.; DEUTSCH, C. V. Mineral resource estimation [S. l.]: Springer, 2014.
- VIEIRA, F. W. R Gênese das mineralizações auríferas da mina de Raposos. In: SIMPÓSIO DE GEOLOGIA DE MINAS GERAIS, 4., 1987, Belo Horizonte Anais […]. Belo Horizonte: SBG, 1987. v.7, p. 358-368.
Publication Dates
-
Publication in this collection
29 Mar 2021 -
Date of issue
Apr-Jun 2021
History
-
Received
04 Mar 2020 -
Accepted
04 Jan 2021