RESUMO
Este artigo investiga a relação entre educação e desigualdade na distribuição de renda usando dados de 5.565 cidades brasileiras. Foi construído um índice educacional geral composto por 24 indicadores básicos. A desigualdade na distribuição de renda foi representada pelo índice de Gini. A análise foi controlada pela renda média domiciliar per capita. Os resultados mostraram que o indicador educacional melhora com um aumento da renda, e piora com um aumento da desigualdade. Uma redução de 0,1 unidade no índice de Gini é equivalente a um aumento de 17% na renda média domiciliar.
Palavras-chave
Educação; Renda; Desigualdade de renda
ABSTRACT
This paper investigates the relationship between education and income inequality using data from 5,565 Brazilian cities. An education composite index combining 24 key indicators was constructed and calculated for each city. Income inequality was measured by the Gini index. The analysis was controlled for mean per capita household income. The results have shown that the education index increases with increasing income, but decreases with increasing inequality. Reduction of 0.1 in the Gini index is equivalent to increasing income by 17%.
Keywords
Education; Income; Income inequality
RESUMEN
Este trabajo investiga la relación entre educación y desigualdad en la distribución del ingreso utilizando datos de 5.565 ciudades brasileñas. Se construyó un índice educativo general compuesto por 24 indicadores básicos. La desigualdad en la distribución del ingreso estuvo representada por el índice de Gini. El análisis fue controlado por el ingreso familiar promedio per cápita. Los resultados mostraron que el indicador educativo mejora con el aumento del ingreso y empeora con el aumento de la desigualdad. Una reducción de 0,1 unidades en el índice de Gini equivale a un aumento del 17% en el ingreso familiar promedio.
Palabras-clave
Educación; Ingresos; Desigualdad de ingresos
Introdução
Diversos autores têm estudado a relação entre a desigualdade na distribuição de renda e indicadores sociais, tais como educação (Wilkinson e Pickett, 2007WILKINSON, R., and PICKETT, K. The problems of relative deprivation: Why some societies do better than others, Social Science and Medicine, v. 65, n. 9, p. 1965-1978, 2007. https://doi.org/10.1016Zj.socscimed.2007.05.041
https://doi.org/10.1016Zj.socscimed.2007...
; Salvato et all, 2010SALVATO, M. A., FERREIRA, P C. G., DUARTE, A. J.M. O impacto da escolaridade sobre a distribuição de renda. Estud. Econ, v. 40, n4. p. 753-791, 2010. https://doi.org/10.1590/S0101-41612010000400001
https://doi.org/10.1590/S0101-4161201000...
; Muller, 2002MULLER, A. Education, income inequality, and mortality: a multiple regression analysis, British Medical Journal, v. 324, p. 1-4, 2002. https://doi.org/10.1136/bmj.324.7328.23
https://doi.org/10.1136/bmj.324.7328.23...
), saúde (Celeste e Nadanovsky, 2010CELESTE RK; NADANOVSKY, P Aspectos relacionados aos efeitos da desigualdade de renda na saúde: mecanismos contextuais. Cien. Saúde Colet. v. 15, n. 5, p. 2507-2519, 2010. https://doi.org/10.1590/S1413-81232010000500025
https://doi.org/10.1590/S1413-8123201000...
; Wilkinson, 1992WILKINSON, R. G. Income distribution and life expectancy. Britsh Medical Journal., v. 304, n. 6820, p. 165-168, 1992. https://doi.org/10.1136/bmj.304.6820.165
https://doi.org/10.1136/bmj.304.6820.165...
), mobilidade social (Autor, 2014AUTOR, D. H. Skills, education, and the rise of earnings inequality among the “other 99 percent”. Science, v. 344, n. 6186, p. 843-851, 2014. https://doi.org/10.1126/science.1251868
https://doi.org/10.1126/science.1251868...
), desenvolvimento infantil (Pickett e Wilkinson, 2015aPICKETT, K. E., and R. G. WILKINSON, R. G.. Income inequality and health: A causal review. Social Science & Medicine, v. 128, p. 316-326 (2015a). https://doi.org/10.1016/j.socscimed.2014.12.031
https://doi.org/10.1016/j.socscimed.2014...
), entre outros.
Como regra, para países com características similares, inclusive quanto à renda per capita, quanto mais desigual for sua distribuição, piores são os indicadores sociais. Afinal, uma má distribuição de renda tem implicações bastante sérias em um país, como a falta de coesão social ou a quantidade de pessoas vivendo abaixo de um determinado nível de pobreza.
Este trabalho tem como objetivo avaliar quantitativamente a relação entre a distribuição de renda e as características educacionais dos municípios brasileiros. Para tal, determinou-se um indicador geral que pudesse caracterizar o desenvolvimento educacional de cada município e estudou-se a variação desse indicador com a renda média domiciliar per capita e com o índice de Gini, um indicador da desigualdade na distribuição da renda1 1 O índice de Gini varia entre zero e um. Quanto mais próximo de um, pior a distribuição de renda. Em geral, índices de Gini acima de 0,5 indicam péssima distribuição de renda. Cerca da metade das cidades brasileiras está nessa situação. Valores abaixo de 0,3 indicam excelentes distribuições de renda. que está entre os mais usados nas análises econométricas e sociais.
O procedimento desenvolvido neste trabalho permitiu determinar a relação entre a desigualdade da distribuição de renda e o indicador de desenvolvimento educacional, tanto no país como um todo como em cada um dos estados.
Dados usados
As análises foram feitas com dados de 5.565 municípios brasileiros para os quais há informações educacionais disponíveis no Atlas do Desenvolvimento Humano do Brasil 2013 (Atlas, 2013ATLAS. Programa das Nações Unidas para o Desenvolvimento; Instituto de Pesquisa Econômica Aplicada; Fundação João Pinheiro. Atlas do Desenvolvimento Humano no Brasil 2013.). As informações sistematizadas e divulgadas no Atlas correspondem a mais de 200 indicadores de demografia, educação, renda, trabalho, habitação e vulnerabilidade, com dados extraídos dos Censos Demográficos de 1991, 2000 e 2010.
Com o objetivo de se obter um indicador amplo do desenvolvimento educacional de cada município, foram utilizados vários indicadores específicos que pudessem revelar tanto a situação educacional mais recente, tais como as taxas de inclusão nos anos iniciais do ensino, como a situação educacional passada, no caso das taxas de analfabetismo adulto. Esses indicadores, que representam uma combinação de indicadores de acesso, percurso, permanência, resultados etc, estão especificados no Apêndice A. Para evitar redundância, optou-se por usar um subconjunto das informações disponíveis, de modo a incluir todas as características relevantes da educação escolar sem, entretanto, usar dados que poderiam se repetir. Por exemplo, ao se usar as taxas de analfabetismo dos 18 aos 24 anos e a mesma taxa para a faixa etária de 25 anos ou mais, foi descartada a taxa de analfabetismo aos 18 anos ou mais, uma vez que haveria uma grande correlação entre os indicadores, sendo redundante usá-los simultaneamente.
Adequação dos dados
O indicador geral do nível educacional de cada cidade foi estimado com base nos indicadores listados no Apêndice A.
Cada um dos indicadores para cada cidade é identificado a seguir por xij, onde o índice i indica o município e o índice j, o indicador.
Essas variáveis podem ter faixas de variação muito diferentes. Por exemplo, enquanto a taxa de analfabetismo de jovens de 18 a 24 anos varia entre zero e cerca de 5%, as taxas de frequência escolar em alguns níveis de ensino variam em uma faixa mais do que dez vezes maior. Portanto, usar como indicador geral uma combinação linear simples das variáveis pode fazer com que indicadores que tenham faixas de variação pequenas, ainda que importantes, não tenham peso significativo no indicador geral.
Para que todos os indicadores considerados pudessem ter peso equivalente, cada uma das variáveis para cada município, xij, foi modificada segundo a Eq. 1:
onde xj é o valor médio do indicador educacional j calculado considerando todos os valores xij,
sendo m a quantidade de municípios. O desvio padrão de xj, σj, foi calculado da forma usual,
O indicador geral de educação do município identificado pelo subscrito i foi calculado pela média simples de todos os valores tij, ti. No cálculo dessa média, foi tomado o cuidado para que os indicadores fossem considerados com o sinal positivo quando um maior valor tem significado positivo, como, por exemplo, as taxas de inclusão nos diferentes níveis de ensino, e negativo no caso contrário, como, por exemplo, as taxas de analfabetismo.
Adotou-se o valor médio ti como o indicador de desenvolvimento educacional do município i. Esse indicador foi calculado para os 5.565 municípios brasileiros, tendo variado entre -3,1 e 1,7. A Tabela 1 mostra as dez cidades com maiores e menores valores do indicador educacional.
Os dez municípios com menores valores para o indicador estão na região Norte do país (AM, PA e RR), têm índices de desenvolvimento humano (IDHM) bastante baixos, e muito deles estão na fronteira do país ou do estado. As cidades que têm indicadores educacionais altos estão nas regiões Sul e Sudeste do país. Algumas delas são bastante pequenas e, portanto, mais sujeitas a apresentarem características peculiares.
Relação funcional entre os indicadores
A parte superior da Fig. 1 mostra o indicador do desenvolvimento educacional e o índice de Gini para cada município. Na parte inferior, a mesma figura mostra aquele indicador e o logaritmo da renda média domiciliar per capita, também para cada município.
Indicador geral para cada uma das 5.565 cidades brasileiras em função do índice de Gini e do logaritmo da renda domiciliar mensal per capita--
onde gi e ri são, respectivamente, o índice de Gini e a renda média domiciliar per capita do município i, e ei um valor aleatório cujo valor esperado é supostamente nulo. Os parâmetros b e c indicam como o valor esperado do indicador educacional de cada município está relacionado com a renda média domiciliar per capita daquele município e de como ela é distribuída. O ajuste dos parâmetros foi feito usando-se o método dos mínimos quadrados (Helene, 2012HELENE, O. (2012). Métodos dos Mínimos Quadrados Com Formalismo Matricial. Ed. LF.).
.
Após o ajuste dos parâmetros, o valor esperado ti do indicador educacional de cada município foi calculado e o desvio padrão σ de cada dado ti foi estimado por:
sendo n a quantidade de dados disponíveis (5.565 no caso da totalidade dos municípios brasileiros). A partir da estimativa das variâncias dos dados, as variâncias e covariâncias dos parâmetros ajustados foram estimadas da forma usual (Helene, 2012HELENE, O. (2012). Métodos dos Mínimos Quadrados Com Formalismo Matricial. Ed. LF.).
Resultados
-
Brasil
Quando considerados os 5.565 municípios brasileiros com dados disponíveis na referência (Atlas, 2013ATLAS. Programa das Nações Unidas para o Desenvolvimento; Instituto de Pesquisa Econômica Aplicada; Fundação João Pinheiro. Atlas do Desenvolvimento Humano no Brasil 2013.), os valores ajustados para os parâmetros (e seus respectivos desvios padrões) foram:
O fato do parâmetro b ser negativo indica que quanto maior for o índice de Gini, dada a mesma condição quanto à renda média domiciliar por pessoa, pior é o indicador educacional.
O fato do parâmetro ser positivo indica que quanto maior a renda domiciliar média por pessoa em um município, melhor seu indicador educacional, um resultado até mesmo intuitivo.
-
Estados
A mesma análise foi feita para cada um dos estados brasileiros. Entretanto, antes de apresentar resultados resumidos para os vários estados, o que é feito mais adiante, vale a pena examinar um caso específico, o do Estado de São Paulo, que revela alguns aspe
ctos interessantes da análise. Embora haja uma clara correlação entre o indicador educacional e a renda nos municípios desse estado, como mostra a Fig. 2, parece não haver correlação significativa com o índice de Gini, pelo menos em uma inspeção visual. Uma análise precipitada poderia levar à conclusão que a desigualdade na distribuição de renda não tem efeito no indicador do desenvolvimento educacional dos municípios paulistas. Entretanto, essa conclusão está errada.Figura 2
Indicador geral para cidades do Estado de São Paulo em função do índice de Gini e da renda domiciliar mensal per capita.
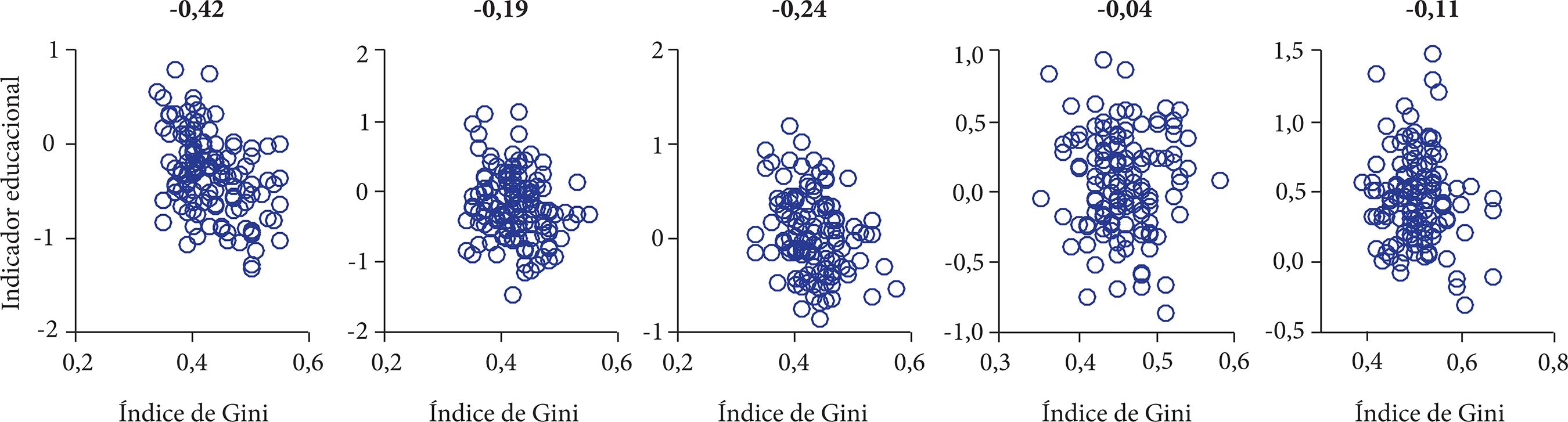
É possível perceber o efeito negativo da desigualdade na distribuição de renda sobre o indicador educacional dos municípios quando estes são separados em grupos com rendas aproximadamente iguais. Isso é mostrado na Fig. 3: em cada um desses grupos o coeficiente de correlação entre desigualdade e educação é negativo. Nos casos mostrados nos dois últimos gráficos da Fig. 3 os coeficientes de correlação são muito pequenos em termos absolutos, não permitindo uma conclusão. Entretanto, nos três primeiros gráficos os níveis de significância são bastante expressivos; mesmo naquele cujo coeficiente de correlação é, em termos absolutos, o menor deles, 0,19, o nível de significância é p = 1,6%.
Figura 3
Indicador educacional e índice de Gini para as cidades paulistas separadas em cinco grupos homogêneos de renda. Acima de cada gráfico aparece o coeficiente de correlação entre as duas variáveis.
Quando é feito o ajuste dos parâmetros a, b e c aos dados dos municípios paulistas, os resultados obtidos são:
Como se percebe, o coeficiente é negativo, confirmando o fato que quanto maior o índice de Gini, pior o indicador educacional. Portanto, é reforçada a hipótese que a correlação positiva entre o índice de Gini e o indicador educacional é devida ao fato que, em São Paulo, há uma tendência de que a renda seja mais mal distribuída quanto maior ela for.
A mesma análise foi feita para cada um dos demais 25 estados do país e os coeficientes obtidos nos ajustes aparecem no Apêndice B. Como regra, em cada um dos estados os indicadores de desenvolvimento educacionais crescem com o aumento da renda domiciliar média per capita dos municípios e decrescem com o aumento da desigualdade.
O fato que os parâmetros de regressão dos vários estados são estatisticamente diferentes quando comparados entre si pode indicar que outras características dos estados devam ser consideradas no modelo adotado e merece um exame posterior.
Paraíba, Bahia, Espírito Santo, e Rio de Janeiro são os demais estados, além de São Paulo, nos quais a correlação entre o índice de Gini e o indicador educacional é positiva, sugerindo que quanto mais desigualmente for distribuída a renda melhor o desempenho educacional. Entretanto, como no caso paulista, isso ocorre porque a correlação entre a renda e o índice de Gini nesses estados é muito grande. De fato, esses estados, juntamente com São Paulo, são aqueles com maiores correlações entre a desigualdade na distribuição de renda e a renda média domiciliar nos municípios: quanto maior a renda média dos munícipes, mais desigualmente ela é distribuída. Mas, como no caso paulista, quando se examinam os coeficientes de correlação condicional entre educação e desigualdade, eles se tornam negativos, indicando que uma melhor distribuição de renda está associada a um melhor padrão educacional. Este último fato é confirmado pelos valores obtidos para os parâmetros b mostrados no apêndice B, todos negativos.
Discussão
A adequação do modelo adotado para estimar o indicador de desenvolvimento educacional dos municípios a partir da renda média municipal per capita e do índice de Gini pode ser observada na Fig. 4. Nessa figura aparecem os valores observados (abscissa) e calculado (ordenada) daquele indicador. Um teste do coeficiente de determinação R2 entre as duas grandezas representadas nessa figura leva a um valor-p praticamente nulo.
Comparação entre os valores observados e calculados para o indicador de desenvolvimento educacional para os 5.565 municípios brasileiros.
A existência de correlação entre indicadores sociais e econômicos não revelam, necessariamente, uma relação de causa e efeito. Mesmo que essa relação exista, apenas a correlação não é suficiente para estabelecer qual é a causa e qual é o efeito. Entretanto, vários pesquisadores têm buscado provas e elaborado argumentos com o objetivo de mostrar que a relação entre uma má distribuição de renda e maus indicadores sociais pode ser direta ou intermedida pela perda de coesão social provocada pela desigualdade (Wilkinson e Pickett, 2007WILKINSON, R., and PICKETT, K. The problems of relative deprivation: Why some societies do better than others, Social Science and Medicine, v. 65, n. 9, p. 1965-1978, 2007. https://doi.org/10.1016Zj.socscimed.2007.05.041
https://doi.org/10.1016Zj.socscimed.2007...
; Celeste e Nadanovsky, 2010CELESTE RK; NADANOVSKY, P Aspectos relacionados aos efeitos da desigualdade de renda na saúde: mecanismos contextuais. Cien. Saúde Colet. v. 15, n. 5, p. 2507-2519, 2010. https://doi.org/10.1590/S1413-81232010000500025
https://doi.org/10.1590/S1413-8123201000...
; Pickett e Wilkinson, 2015bPICKETT, K. E., WILKINSON, R. G.. The Ethical and Policy Implications of Research on Income Inequality and Child Well-being. Pediatrics, v. 13, Supplement 2: S39-S47 (2015b). https://doi.org/10.1542/peds.2014-3549E
https://doi.org/10.1542/peds.2014-3549E...
). Além dessa interpretação, há trabalhos que revelam que tanto a perda de coesão social como a má distribuição de renda e os indicadores sociais negativos têm uma causa comum relacionada ao modo de produção capitalista, em especial em sua fase neoliberal atual (Coburn, 2015COBURN, D. Income inequality, welfare, class and health: A comment on Pickett and Wilkinson, Social Scienece & Medicine v. 15, n 146, p. 228-232, 2015. https://doi.org/10.1016/j.socscimed.2015.09.002
https://doi.org/10.1016/j.socscimed.2015...
).
Considerando os resultados deste trabalho, é possível conjecturar que uma melhora do indicador de desenvolvimento educacional com o aumento da renda média familiar per capita e com uma distribuição de renda menos desigual refletem relações de causa e efeito, o que poderia ser considerado na elaboração de políticas públicas educacionais.
A Eq. 6 mostra que variações no índice de Gini, Δg, e na renda média domiciliar per capita dos municípios, Δr, têm mesmos efeitos no indicador educacional se:
Quando são considerados todos os 5.565 municípios brasileiros, esta equação indica que a variação no indicador geral de educação associada a uma variação do índice de Gini de 0,1 é equivalente a uma variação da ordem de 17% na renda domiciliar média per capita.
A relação entre os parâmetros variam entre os vários estados do país (Apêndice B). Entretanto, em todos eles, essa relação indica que uma melhora na distribuição de renda está associada a uma melhora no desempenho educacional.
Como a renda média de um município está relacionada com o nível escolar de sua população, a forte dependência do desempenho escolar com a renda média faz com que haja um círculo vicioso. A baixa renda hoje implica em baixo desempenho educacional (Castro, 2009CASTRO, J. A. Evolução e desigualdade na educação brasileira. Educ. Soc., v. 30, n. 108, p. 673-697, 2009. https://doi.org/10.1590/S0101-73302009000300003
https://doi.org/10.1590/S0101-7330200900...
) e, portanto, baixa renda no futuro, quando a população hoje em idade escolar passar a fazer parte da população economicamente ativa. Assim, se os coeficientes obtidos nos ajustes feitos refletirem uma relação de causa e efeito, uma política que atue na direção de reduzir a desigualdade na distribuição de renda pode ter efeitos positivos tanto no presente, sob a forma de um melhor desempenho educacional provocada, possivelmente, por uma melhor coesão social e por uma menor proporção de pessoas vivendo em estado de pobreza, como no futuro, levando a um aumento da renda média do município.
A extensão do presente estudo para resultados de censos anteriores poderá fornecer novas informações sobre a relação entre educação e os indicadores econômicos aqui analisados. Inclusive, deverá ser interessante verificar se essa relação se alterou ao longo do tempo e, em especial, examinar o que ocorreu no período em que houve uma perceptível melhora na distribuição de renda no país (Helene, 2010HELENE, O. (2010). Fitting Lorenz curves. Econ. Lett., 108: p. 153-155, 2010. https://doi.org/10.1016/j.econlet.2010.05.010
https://doi.org/10.1016/j.econlet.2010.0...
).
Como conclusão, podemos afirmar que uma análise estatística detalhada pode indicar vários aspectos que uma análise parcial não permite. Como exemplo, a indicação que melhores distribuições de renda estão associadas a melhores desempenhos educacionais dos municípios foi claramente verificada. Entretanto, como ilustrado no caso do Estado de São Paulo, e também verificado em outros estados (Paraíba, Bahia, Espírito Santo e Rio de Janeiro), essa correlação pode não ser percebida em uma análise superficial, pois é escondida pela alta correlação entre distribuição de renda e renda média.
Outro aspecto a concluir é o fato de que um indicador baseado na combinação de vários indicadores parciais pode revelar aspectos gerais do desenvolvimento educacional que cada um deles não pode mostrar. Uma vez obtida essa análise geral, podemos investigar qual ou quais indicadores particulares mais comprometem o desenvolvimento educacional de um município. Esse aspecto, embora não central no presente trabalho, pode sugerir outras abordagens complementares.
Finalmente, este trabalho permite concluir que uma melhora no desempenho educacional de um município pode estar associada tanto a uma melhora na distribuição de renda como a um aumento na renda média. Ou seja, para qualquer valor da renda domiciliar per capita, pelo menos dentro dos valores que os municípios brasileiros permitem examinar, a melhor distribuição de renda está associada à um melhor desempenho educacional.
Notas
-
O índice de Gini varia entre zero e um. Quanto mais próximo de um, pior a distribuição de renda. Em geral, índices de Gini acima de 0,5 indicam péssima distribuição de renda. Cerca da metade das cidades brasileiras está nessa situação. Valores abaixo de 0,3 indicam excelentes distribuições de renda.
-
Este artigo foi elaborado por pesquisadores do Instituto de Física da Universidade de São Paulo, inserindo-se em uma linha de trabalho na qual são adotadas técnicas quantitativas visando contribuir para o entendimento de questões sociais.
Notas
-
1
O índice de Gini varia entre zero e um. Quanto mais próximo de um, pior a distribuição de renda. Em geral, índices de Gini acima de 0,5 indicam péssima distribuição de renda. Cerca da metade das cidades brasileiras está nessa situação. Valores abaixo de 0,3 indicam excelentes distribuições de renda.
Apêndices
Apêndice A. Variáveis consideradas para o cálculo do indicador de desenvolvimento educacional.A descrição das variáveis é exatamente a mesma que aparece na referência (Atlas, 2013ATLAS. Programa das Nações Unidas para o Desenvolvimento; Instituto de Pesquisa Econômica Aplicada; Fundação João Pinheiro. Atlas do Desenvolvimento Humano no Brasil 2013.).
-
Número médio de anos de estudo que uma geração de crianças que ingressa na escola deverá completar ao atingir 18 anos de idade, se os padrões atuais se mantiverem ao longo de sua vida escolar.
-
Razão entre a população de 11 a 14 anos de idade analfabeta e o total de pessoas nesta faixa etária. (Consideram-se analfabetas pessoas que não sabem ler nem escrever um bilhete simples.)
-
Razão entre a população de 15 a 17 anos de idade analfabeta e o total de pessoas nesta faixa etária.
-
Razão entre a população analfabeta de 18 a 24 anos de idade e o total de pessoas nesta faixa etária.
-
Razão entre a população analfabeta de 25 anos ou mais de idade e o total de pessoas nesta faixa etária.
-
Razão entre o número de pessoas de 6 a 14 anos frequentando o ensino fundamental regular seriado sem atraso idadesérie e o número total de pessoas nessa faixa etária frequentando esse nível de ensino.
-
Razão entre o número de pessoas de 15 a 17 anos frequentando o ensino médio regular seriado sem atraso idade-série e o número total de pessoas nessa faixa etária frequentando esse nível de ensino.
-
Razão entre o número total de pessoas de qualquer idade frequentando o ensino fundamental regular seriado e a população na faixa etária de 6 a 14 anos. As pessoas de 6 anos ou mais frequentando a pré-escola foram consideradas como se estivessem no 1º ano do ensino fundamental.
-
Razão entre o número total de pessoas de qualquer idade frequentando o ensino médio regular seriado e a população na faixa etária de 15 a 17 anos. (As pessoas frequentando a 4ª série do ensino médio foram consideradas como tendo concluído esse nível de ensino.)
-
Razão entre o número total de crianças de até 5 anos de idade frequentando a pré-escola e a população nessa mesma faixa etária. As pessoas de 6 anos ou mais frequentando a pré-escola foram consideradas como se estivessem no 1º ano do ensino fundamental.
-
Razão entre o número total de pessoas de qualquer idade frequentando o ensino superior (graduação, especialização, mestrado ou doutorado) e a população na faixa etária de 18 a 24 anos.
-
Razão entre a população de 0 a 3 anos de idade que estava frequentando a escola, em qualquer nível ou série, e a população total nesta faixa etária.
-
Razão entre a população de 4 a 5 anos de idade que estava frequentando a escola, em qualquer nível ou série, e a população total nesta faixa etária.
-
Razão entre população de 6 a 17 anos de idade que estava frequentando a escola, em qualquer nível ou série, e a população total nesta faixa etária.
-
Razão entre a população de 18 a 24 anos de idade que estava frequentando a escola, em qualquer nível ou série, e a população total nesta faixa etária.
-
Razão entre a população de 25 a 29 anos de idade que estava frequentando a escola, em qualquer nível ou série, e a população total nesta faixa etária.
-
Razão entre a população de 4 a 5 anos de idade frequentando o ensino fundamental regular seriado e o total de pessoas nesta faixa etária.
-
Razão entre a população de 12 a 14 anos de idade que frequenta os quatro anos finais do fundamental ou que já concluiu o fundamental e a população total nesta faixa etária.
-
Razão entre a população de 15 a 17 anos de idade que concluiu o ensino fundamental e o total de pessoas nesta faixa etária.
-
Razão entre a população de 16 a 18 anos de idade que já concluiu o ensino fundamental e o total de pessoas nesta faixa etária.
-
Razão entre a população de 18 a 24 anos de idade que concluiu o ensino fundamental e o total de pessoas nesta faixa etária
-
Razão entre a população de 25 anos ou mais de idade que concluiu o ensino fundamental e o total de pessoas nesta faixa etária.
-
Razão entre a população de 18 a 24 anos de idade que concluiu o ensino médio.
-
Razão entre a população de 25 anos ou mais de idade que concluiu o ensino médio e o total de pessoas nesta faixa etária.
Referências
- ATLAS. Programa das Nações Unidas para o Desenvolvimento; Instituto de Pesquisa Econômica Aplicada; Fundação João Pinheiro. Atlas do Desenvolvimento Humano no Brasil 2013.
- AUTOR, D. H. Skills, education, and the rise of earnings inequality among the “other 99 percent”. Science, v. 344, n. 6186, p. 843-851, 2014. https://doi.org/10.1126/science.1251868
» https://doi.org/10.1126/science.1251868 - CASTRO, J. A. Evolução e desigualdade na educação brasileira. Educ. Soc., v. 30, n. 108, p. 673-697, 2009. https://doi.org/10.1590/S0101-73302009000300003
» https://doi.org/10.1590/S0101-73302009000300003 - CELESTE RK; NADANOVSKY, P Aspectos relacionados aos efeitos da desigualdade de renda na saúde: mecanismos contextuais. Cien. Saúde Colet. v. 15, n. 5, p. 2507-2519, 2010. https://doi.org/10.1590/S1413-81232010000500025
» https://doi.org/10.1590/S1413-81232010000500025 - COBURN, D. Income inequality, welfare, class and health: A comment on Pickett and Wilkinson, Social Scienece & Medicine v. 15, n 146, p. 228-232, 2015. https://doi.org/10.1016/j.socscimed.2015.09.002
» https://doi.org/10.1016/j.socscimed.2015.09.002 - HELENE, O. (2010). Fitting Lorenz curves. Econ. Lett., 108: p. 153-155, 2010. https://doi.org/10.1016/j.econlet.2010.05.010
» https://doi.org/10.1016/j.econlet.2010.05.010 - HELENE, O. (2012). Métodos dos Mínimos Quadrados Com Formalismo Matricial. Ed. LF.
- MULLER, A. Education, income inequality, and mortality: a multiple regression analysis, British Medical Journal, v. 324, p. 1-4, 2002. https://doi.org/10.1136/bmj.324.7328.23
» https://doi.org/10.1136/bmj.324.7328.23 - PICKETT, K. E., and R. G. WILKINSON, R. G.. Income inequality and health: A causal review. Social Science & Medicine, v. 128, p. 316-326 (2015a). https://doi.org/10.1016/j.socscimed.2014.12.031
» https://doi.org/10.1016/j.socscimed.2014.12.031 - PICKETT, K. E., WILKINSON, R. G.. The Ethical and Policy Implications of Research on Income Inequality and Child Well-being. Pediatrics, v. 13, Supplement 2: S39-S47 (2015b). https://doi.org/10.1542/peds.2014-3549E
» https://doi.org/10.1542/peds.2014-3549E - SALVATO, M. A., FERREIRA, P C. G., DUARTE, A. J.M. O impacto da escolaridade sobre a distribuição de renda. Estud. Econ, v. 40, n4. p. 753-791, 2010. https://doi.org/10.1590/S0101-41612010000400001
» https://doi.org/10.1590/S0101-41612010000400001 - WILKINSON, R. G. Income distribution and life expectancy. Britsh Medical Journal., v. 304, n. 6820, p. 165-168, 1992. https://doi.org/10.1136/bmj.304.6820.165
» https://doi.org/10.1136/bmj.304.6820.165 - WILKINSON, R., and PICKETT, K. The problems of relative deprivation: Why some societies do better than others, Social Science and Medicine, v. 65, n. 9, p. 1965-1978, 2007. https://doi.org/10.1016Zj.socscimed.2007.05.041
» https://doi.org/10.1016Zj.socscimed.2007.05.041
Datas de Publicação
-
Publicação nesta coleção
06 Mar 2020 -
Data do Fascículo
2020
Histórico
-
Recebido
03 Maio 2019 -
Aceito
12 Dez 2019