Resumos
É muito comum perceber, nos livros didáticos, na própria fala do professor, o uso da negação como elemento essencial no ensino de matemática. A negação está presente, por exemplo, na proposição contrapositiva, no não-exemplo, no contraexemplo e na complementaridade. Discutiremos, neste texto, possibilidades de que o uso da negação e dessas formas de negação encontre, nos registros de representação semiótica de Duval, uma base de sustentação e possa apontar caminhos para a aprendizagem matemática.
Negação; Contrapositiva; Contraexemplo; Não-exemplo; Complementar; Registros de representação semiótica; Aprendizagem matemática
It is very common to observe in teaching materials and even in teachers´ discourse the use of negation as an essential element in the teaching of mathematics. Negation is present, for example, in counter-positive propositions, in non-examples, in counterexamples and in complementarity. This article discusses the possible uses of negation and how these forms of negation can be not only be supported by Duval´s registers of semiotic representations, but also find paths to the learning of mathematics.
Negation; Counterpositive; Counterexample; Non-example; Complementarity; Registers of semiotic representations; Learning mathematics
Estudo das formas de negação no processo de ensino da matemática: ponto de encontro com os registros de representação semiótica
A study of forms of negation in the teaching of mathematics: a meeting with the registers of semiotic representations
Méricles Thadeu MorettiI; Célia Finck BrandtII; Patrícia Lanzini FrancoIII
IDepartamento de Matemática, Universidade Federal de Santa Catarina, Campus Universitário. Bairro Trindade, Florianópolis, SC, Brasil. 88.040-900, E-mail: mericles@mtm.ufsc.br IIUniversidade Estadual de Ponta Grossa. Ponta Grossa, PR, Brasil
IIIColégio Energia. Balneário Camboriú, SC, Brasil
RESUMO
É muito comum perceber, nos livros didáticos, na própria fala do professor, o uso da negação como elemento essencial no ensino de matemática. A negação está presente, por exemplo, na proposição contrapositiva, no não-exemplo, no contraexemplo e na complementaridade. Discutiremos, neste texto, possibilidades de que o uso da negação e dessas formas de negação encontre, nos registros de representação semiótica de Duval, uma base de sustentação e possa apontar caminhos para a aprendizagem matemática.
Palavras-chave: Negação. Contrapositiva. Contraexemplo. Não-exemplo. Complementar. Registros de representação semiótica. Aprendizagem matemática.
ABSTRACT
It is very common to observe in teaching materials and even in teachers´ discourse the use of negation as an essential element in the teaching of mathematics. Negation is present, for example, in counter-positive propositions, in non-examples, in counterexamples and in complementarity. This article discusses the possible uses of negation and how these forms of negation can be not only be supported by Duval´s registers of semiotic representations, but also find paths to the learning of mathematics.
Keywords: Negation. Counterpositive. Counterexample. Non-example. Complementarity. Registers of semiotic representations. Learning mathematics.
Introdução
A compreensão de como o aluno aprende e a incessante busca de métodos e técnicas que facilitem o processo de ensino-aprendizagem de matemática continuam alvo de diversas discussões e pesquisas em Educação Matemática. Uma dessas técnicas utilizadas por professores no processo de ensino é aquela que lança mão de certas formas da negação no discurso em sala de aula. São exemplos: a proposição contrapositiva, não-exemplo, contraexemplo e complementar. Observamos o uso da negação e dessas diferentes formas de negação com bastante frequência em definições e teoremas matemáticos.
O professor, por vezes, apresenta, aos alunos, casos que não se aplicam a uma definição com o objetivo de sedimentá-la. Podemos-se citar, como exemplo, a definição "um cilindro reto é denominado equilátero quando a medida do diâmetro de sua base é igual a medida da sua altura", seguida de alguns não-exemplos de cilindros equiláteros: "[...] portanto, um canudinho de refrigerante não descreve um cilindro equilátero, nem um cabo de vassoura e muito menos um disco de pizza".
Situações de usos da negação e das formas de negação por professores "do que não é" para caracterizar "o que é" são mais comuns do que se pode pensar nas aulas de matemática, e procuram caracterizar o objeto matemático de uma outra maneira. Elas são utilizadas com o objetivo de levar o aluno à compreensão de uma definição, por exemplo, por meio de opções que a ela não se aplicam. Uma das ideias é pensar que se "isto não é" se pode concluir que do restante "tudo é". Percebemos, aí, a presença da noção de complementaridade, que permite ser possível chegar ao objeto que se deseja pelo que ele não é. Mas o complementar referencia o objeto pretendido? Pode ser considerado como representação deste objeto?
Uma outra ideia é o uso da proposição contrapositiva. Veremos que este uso pode ser bastante proveitoso, pois possibilita alterar o quadro cognitivo da situação de ensino, quando o registro de representação é modificado, sem alterar a referência ao objeto em questão, uma vez que a proposição direta e a contrapositiva são logicamente equivalentes.
Neste texto, retomamos um estudo desenvolvido por Franco (2008), que utiliza, sobretudo, os CDs de aulas gravadas e material impresso por professores do Sistema de Ensino Energia (2006, 2007a, 2007b). Tal estudo trata das possibilidades de utilização das formas de negação para a aprendizagem da matemática, com subsídios teóricos na lógica formal e nas representações semiótica de Duval (1988, 1993, 1995, 1996, 2003). Apresentaremos, em um primeiro momento, as ideias principais da teoria semiótica de aprendizagem matemática desenvolvida por este autor, para, em seguida, tratar da negação e de algumas formas de negação no ensino de matemática: a contrapositiva, a complementaridade, não-exemplo e contraexemplo. Posteriormente, descreveremos possíveis benefícios, equívocos e perigos relativos à utilização da negação e dessas formas de negação no processo de ensino, para, finalmente, fazermos uma contribuição à hipótese de aprendizagem matemática sustentada por Duval.
Registros de representação semiótica e aprendizagem matemática
Uma contribuição importante para a pesquisa em educação matemática é a teoria de representação semiótica de Duval (1993, 1995), que tem dado suporte para muitas pesquisas no Brasil e em outras partes do mundo. Este autor remarca que o acesso a um dado objeto matemático só é possível por meio da representação desse objeto. Como, então, não confundir o objeto matemático com a sua representação? Para responder a esta questão, Duval (1993) apresenta a hipótese fundamental de aprendizagem para a matemática:
A compreensão (integral) de um conteúdo conceitual repousa sobre a coordenação de ao menos dois registros de representação e esta coordenação manifesta-se pela rapidez e espontaneidade da atividade cognitiva de conversão. (DUVAL, 1993, p. 51)
Tal hipótese é representada, por Duval (1995, p. 67), pelo esquema apresentado na Figura 1.
O esquema da Figura 1 retrata o caso da coordenação entre dois registros de representação. As flechas 1 e 2 correspondem às transformações internas a um registro de representação; as flechas 3 e 4, às transformações externas, ou seja, as conversões por mudanças de registros. As duas flechas inclinadas na parte superior correspondem à distinção clássica de Saussure (2008, p. 79-81) entre significante e significado. Duas são as operações na coordenação entre dois registros: a operação de conversão (flechas 3 e 4) quando se opera entre registros de sistemas semióticos diferentes e a operação de tratamento (flechas 1 e 2) no caso de registros de um mesmo sistema. A passagem entre dois registros pode ter certo grau de dificuldade que depende do que Duval (1988, p. 8) chama de não-congruência semântica:
Duas expressões podem ser sinônimas ou referencialmente equivalentes (elas podem "dizer a mesma coisa", elas podem ser verdadeiras ou falsas conjuntamente) e não serem semanticamente congruentes: neste caso há um custo cognitivo importante para a compreensão.
Para entender um pouco melhor o que este autor quer dizer nesta citação, tomemos o exemplo da frase seguinte: "um pai (p) tem 25 anos a mais do que a idade de seu filho (f)" é semanticamente congruente com a equação "p + f = 25", mas a frase e a equação não são referencialmente equivalentes. Diferente é o caso da equação p f = 25 e a mesma frase, ambas não possuem congruência semântica, mas são referencialmente equivalentes. Já a frase "a diferença entre a idade do pai (p) e a idade do filho (f) é de 25 anos" e "p f = 25" são congruentes e referencialmente equivalentes.
Certas vezes, um objeto matemático se apresenta em uma forma de representação que possui um custo cognitivo muito alto para a realização de raciocínios e procedimentos de cálculo necessários. Então, a possibilidade de se usar outra representação que proporcione tratamentos menos custosos é importante. A atividade de substituição que pode ocorrer entre duas expressões referencialmente equivalentes, além de exibir propriedades diferentes de um objeto, pode caracterizar um "salto" entre duas redes semânticas. Essa troca não ocorre sempre de forma natural e espontânea. O sucesso de tal atividade depende do fenômeno da não-congruência semântica, que mede a distância cognitiva entre essas duas representações, sejam elas pertencentes ou não ao mesmo sistema semiótico de representação. As representações não congruentes solicitam atividades intelectuais igualmente diferentes. Duval (1988, p. 11-12, grifo do autor) explica que "a equivalência referencial não é uma razão suficiente para reunir em uma mesma rede semântica e, a fortiori, para assegurar a evidência imediata da substituição de uma expressão em outra não-congruente".
Quando o aluno se depara com um objeto matemático, inevitavelmente, ele terá necessidade de trabalhar com as representações desse objeto. As apreensões de definições, postulados ou teoremas matemáticos requerem o uso dessas representações, as quais estão intimamente ligadas às operações de conversão e tratamento. É importante observar que os tratamentos estão relacionados à forma, e não ao conteúdo do objeto matemático. Por exemplo, a operação 0,20 + 0,25 = 0,45 requer tratamento na forma de representação decimal, enquanto que, no caso 1/5 + 1/4 = 9/20, o tratamento se dá na forma fracionária são conhecimentos ou técnicas diferentes que precisam ser mobilizadas para que a soma possa ser efetuada. Já para a passagem da forma decimal para a fracionária ou da forma fracionária para a decimal, são outras noções exigidas, diferentes daquelas encontradas nesses tratamentos, e estão relacionadas diretamente à ideia mesmo de fração.
Moretti (2002) argumenta que a escola se preocupa em criar novas formas de representação com a intenção de encontrar, para cada conceito matemático, uma "boa representação", que leve o aluno, de forma suficiente, à compreensão, mas adverte que não existe uma "boa representação", pois cada registro evidencia algumas características e pode ocultar outras. Duval (1993, p. 47) afirma que "qualquer registro é sempre incompleto em relação ao objeto denotado", é a articulação entre registros que constitui uma condição de acesso à compreensão da matemática, e não o enclausuramento: a coordenação entre registros de representação não é natural aos alunos, que podem não reconhecer um mesmo objeto em representações que são dadas em sistemas semióticos diferentes ou até no mesmo sistema semiótico. Por esta razão, é fundamental a diversidade de registros e as operações entre eles para se evitar que o aluno conheça apenas uma representação de um dado objeto e, com isto, aumente a possibilidade de confusão entre a representação do objeto e o objeto representado.
Duval (1993, 2003) assinala outras vantagens da diversidade dos registros de representação semiótica. Uma primeira vantagem tem a ver com economia de tratamento. Havendo vários registros de representação, é possível ocorrer mudança entre eles, e estas mudanças poderão ser mais econômicas e potencializadas; há uma ampliação de possibilidades de trocas e, por conseguinte, um aumento, também, na escolha do procedimento de resolução mais econômico para certo tipo problema.
A segunda vantagem refere-se à complementaridade dos registros. Esta resposta está baseada fortemente no que certo tipo de sistema semiótico pode oferecer. Por exemplo, a linguagem discursiva não oferece as mesmas possibilidades que podem oferecer um diagrama, tabela, gráfico. Isto quer dizer que:
As representações diferentes de um mesmo objeto, não têm evidentemente o mesmo conteúdo. Cada conteúdo é comandado por um sistema pelo qual a representação foi produzida. Daí a consequência de que cada representação não apresenta as mesmas propriedades ou as mesmas características do objeto. Nenhum sistema de representação pode produzir uma representação cujo conteúdo seja completo e adequado ao objeto representado. (DUVAL, 1993, p. 18)
As pesquisas que tomam como fundamento os registros de representação semiótica de Duval assumem, por princípio, a hipótese de aprendizagem representada na Figura 1.
As formas de negação
A utilização das formas de negação para a aprendizagem da matemática pode se justificar, simplesmente, pela possibilidade de produção de novos registros de representação semiótica de objetos matemáticos. A contrapositiva, complementaridade, não-exemplo e contraexemplo, denominados neste texto, simplesmente, de formas de negação, são possibilidades de ensino fundamentadas com todo rigor na lógica formal, e que permitem mudar uma afirmação na substituição de representações.
A negação é uma operação lógica que transforma o valor-verdade de uma proposição que possui valor-verdade verdadeiro [V] em uma proposição com valor-verdade falso [F]; e uma proposição com valor-verdade falso [F] em uma proposição com valor-verdade verdadeiro? [V]. Quer dizer, a partir de uma proposição p qualquer, sempre podemos construir outra denominada negação de p, indicada por ~p.
A negação de uma proposição pode se dar de diferentes formas equivalentes. Na linguagem natural, é possível exemplificar: para a frase "x tem menos de 18 anos", a negação poderá ser "Não é verdade que x tem menos de 18 anos" ou "x tem 18 anos ou x tem mais de 18 anos" ou, ainda, "x não tem menos de 18 anos". Na linguagem formal, a negação tem as formas seguintes: "x > 18" ou "x = 18" ou "x >18".
O uso da negação no interior da lógica matemática se caracteriza, sobretudo, pela "lei da dupla negação": ~(~p) = p. Negar a negação de uma afirmação retorna à afirmação e, com isso, podemos ter duas proposições escritas em formas diferentes com a mesma referência objetal, mas que podem ter significados distintos. Podemos citar, como exemplo, as afirmações: "Não é verdade que o número x é par" e "O número x é ímpar". As regras da lógica possibilitam o tratamento sobre determinadas representações mudando a forma de uma sentença, sem com isso alterar o seu valor-verdade.
Segundo Duval (1995), para analisar os tratamentos por negação é necessário distinguir dois níveis de negação: o primeiro é aquele constituído de operações elementares que permitem opor os enunciados entre si; o segundo é aquele constituído de uma combinação das operações elementares, de tal forma que, verdadeiramente, se podem definir as regras de transformação de um enunciado a outro de modo a conservar o valor-verdade, "É só neste segundo nível que se pode falar em tratamento discursivo ou lógico por negação" (DUVAL, 1995, p. 147).
As regras da lógica possibilitam construir novas proposições de tipos diferentes mediante o emprego dos símbolos lógicos chamados condicionais: o condicional de implicação "se...então" (símbolo → ou ⇒) e o condicional de dupla implicação "se e somente se" (símbolo → ou ⇔). Para proposição condicional p ⇒ q, podemos ler: "se p então q" ou "p é condi- ção necessária para q" ou "q é condição suficiente para p" ou, ainda, "p implica q". p é chamado antecedente ou hipótese e q é chamado consequente ou conclusão. O condicional de dupla implicação (bicondicional) "p ⇔ q" é equivalente a "p ⇒ q e q ⇒ p".
A sentença proposicional condicional é usada tanto na linguagem natural quanto em raciocínios matemáticos, para dizer que a verdade de q está condicionada à verdade de p. No entanto, uma proposição condicional, do ponto de vista lógico-matemático, é independente de uma relação de causa-efeito entre hipótese e conclusão.
Ducrot (1972, p. 180) chama a atenção para essa relação de dependência entre a hipótese e a conclusão e para o uso ingênuo que os matemáticos fazem da proposição:
Um matemático não teria nenhuma repugnância especial em dizer "se 2 + 2 = 4, então 2 + 3 = 5", pois pode-se conceber que a segunda proposição se demonstre da primeira. Mas ele hesitaria em dizer 'Se 2 + 2 = 4, então 2 não tem raiz quadrada racional', pois a demonstração da segunda proposição, neste caso, não utiliza habitualmente à primeira. Eis, como se sabe uma das razões a impedir que a implicação material dos lógicos traduza adequadamente tanto o se dos matemáticos como o da linguagem comum. Essa implicação pode ser afirmada de qualquer par de proposições, por mais distante que uma esteja da outra, conquanto a primeira não seja verdadeira e a segunda seja falsa.
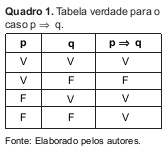
Assim, independentemente da relação causa e efeito entre as proposições, a tabela verdade a seguir define os quatro casos possíveis para a proposição p ⇒ q (Quadro 1).
Podemos perceber que a única combinação em que a sentença condicional é falsa ocorre quando a hipótese é verdadeira e a conclusão é falsa (terceira linha da tabela no Quadro 1). Por exemplo, "Se hoje é segunda-feira, o dia seguinte será terça-feira" é uma sentença condicional sempre verdadeira, qualquer que seja o dia da semana. Já a sentença condicional "Se hoje é segunda-feira, então 2 + 3 = 6" será falsa em qualquer segunda-feira.
Esse último tipo de implicação não é usado em linguagem natural, uma vez que não existe uma relação entre hipótese e conclusão. Porém, o conceito de implicação condicionada está baseado na tabela verdade, ou seja, nos valores lógicos que a hipótese e a conclusão podem assumir.
Barnett (2003) define a recíproca, inversa e contrapositiva de uma afirmação a partir de quatro definições:
Definição 1: A recíproca de uma afirmação é a afirmação formada, permutando-se a hipótese e a conclusão. Assim, a recíproca da afirmação "leões são animais selvagens" é "animais selvagens são leões". [...]
Definição 2: A negativa de uma afirmação é a negação da afirmação. Assim, a negativa da afirmação "um assaltante é um criminoso" é "um assaltante não é um criminoso". [...]
Definição 3: A inversa de uma afirmação é formada negando-se tanto a hipótese quanto a conclusão. Assim, a inversa da afirmação "um assaltante é um criminoso" é "uma pessoa que não é assaltante não é um criminoso". [...]
Definição 4: A contrapositiva de uma afirmação é formada permutando-se a negação da hipótese e a negação da conclusão. Assim, a contrapositiva é a recíproca da inversa e a inversa da recíproca. Assim, a contrapositiva da afirmação "Se você vive na cidade de Nova York, você vive no Estado de Nova York" é "Se você não vive no estado de Nova York, então você não vive na cidade de Nova York". (BARNETT, 2003, p. 279)
Na língua formal, podemos escrever para a proposição p ⇒ q:
Recíproca: q ⇒ p;
Inversa: ~p ⇒ ~q;
Contrapositiva: ~q ⇒ ~p.
Nem sempre podemos dizer que a recíproca de uma afirmação é verdadeira, ou seja, que p ⇒ q é equivalente a q ⇒ p. O mesmo ocorre com p ⇒ q e ~p ⇒~q. Contudo, as proposições p ⇒ q e ~q ⇒ ~p são logicamente equivalentes, ambas são, ao mesmo tempo, falsas ou verdadeiras.
Barnett (2003, p. 279) apresenta essas relações no retângulo de equivalência lógica na Figura 2.
No retângulo de equivalência lógica, as afirmações logicamente equivalentes são aquelas que estão em vértices diagonalmente opostos. Assim, os pares logicamente equivalentes são (a - b) e (c - d).
Na transformação de uma proposição em proposição contrapositiva, chegamos a uma nova proposição logicamente equivalente à proposição inicial, ou seja, a proposição contrapositiva ~q ⇒ ~p tem o mesmo valor-verdade que a proposição condicional p ⇒ q:
O Quadro 2 mostra que as tabelas verdade para os casos p ⇒ q e ~q ⇒ ~p são as mesmas. Podemos explorar quatro situações que nos permitem exemplificar a tabela verdade da implicação e da contrapositiva:
o Primeira situação
p ⇒ q: se 12 é divisível por 6, então 12 é divisível por 3. [V,V,V]
~q ⇒ ~p: se 12 não é divisível por 3, então 12 não é divisível por 6. [F, F,V]
o Segunda situação
p ⇒ q: se 2 x 5 = 10, então 3 é divisor de 10. [V, F, F]
~q ⇒ ~p: se 3 não é divisor de 10, então 2 x 5 ¹ 10. [V, F, F]
o Terceira situação
p ⇒ q: se 5 é múltiplo de 2, então 5 é ímpar. [F, V, V]
~q ⇒ ~p: se 5 é par, então 5 não é múltiplo de 2. [F, V, V]
o Quarta situação
p ⇒ q: se 3 < 2, então 3 = 5. [F, F, V]
~q ⇒ ~p: se 3 ¹ 5 , então 3 > 2. [V, V, V]
[V, V, V] indica, por exemplo, na primeira situação, que p, q e p ⇒ q são verdadeiras.
As proposições p ⇒ q e ~q ⇒ ~p possuem a mesma referência, mesmo que possa haver uma distância muito grande à compreensão entre uma proposição e outra, como é o caso, por exemplo, da definição de função injetora, que discutiremos a seguir.
Seja uma função f real e x1, x2 dois valores quaisquer do seu domínio. Para que f seja injetora, podemos completar a definição de dois modos:
(a) x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
(b) f(x1) = f(x2) ⇒ x1 = x2
A afirmação (b) é a contrapositiva da afirmação (a), elas possuem a mesma referência, mas, evidentemente, não dizem a mesma coisa; a passagem de uma representação para outra não determina, efetivamente, uma conversão, porém solicita do aluno um caminho diferente de compreensão pela negação. Parece que a definição (a) seja a mais preferida dos professores, por estar muito mais próxima da ideia mesmo do que seja a propriedade injetora, e pode ser dita com palavras da seguinte maneira, como a forma encontrada no Sistema de Ensino Energia (2007a): "Uma função f: A → B será denominada injetora, se dois quaisquer domínios distintos corresponderem a duas imagens distintas"1 1 Observamos que o professor utiliza o termo "dois domínios" no lugar de "dois elementos do domínio". . Já não sai assim tão evidente uma frase para a definição (b). No entanto, a contrapositiva é uma possibilidade existente que pode ser amplamente usada nas definições e teoremas de matemática, pois permite mais um caminho para a compreensão e aprendizagem do aluno. Assim, para provar que a função real f(x) = x2 não é injetora, a forma (a) é a que mais se aproxima do tipo de tratamento a ser implementado. No caso da função dada, podemos utilizar, por exemplo, dois pontos distintos x1 = 2 e x2 = -2, aplicar na função, e obter f(2) = f(-2) = 4, para concluir que f não é injetora.
Por outro lado, para provar que f(x) = 2x + 5 é injetora, a definição (b) é a mais conveniente a ser utilizada. De fato, utilizando a forma (b) para esta função, podemos escrever: 2x1 + 5 = 2x2 + 5 ⇒ 2x1 = 2x2 ⇒ x1 = x2. A definição em dois modos diferentes, mas logicamente equivalentes, pode proporcionar mais de um tipo de procedimento na resolução de um determinado problema. O que foi pensado neste caso pode sê-lo, também, para muitas outras situações em matemática.
A exploração do significado de um objeto matemático pode se dar pela exploração das características que ele não possui. Estamos falando da noção de complementaridade. Um exemplo simples da utilização dessa forma de negação baseada na complementaridade são os números pares e ímpares: Consideremos o conjunto dos inteiros Z. O conjunto dos números pares está contido em Z e o conjunto dos números ímpares também. Esses conjuntos são disjuntos, ou seja, não possuem qualquer elemento em comum e podem ser representados na Figura 3.
A noção que buscamos da complementariedade é a mesma que responde à questão: dado o universo (no caso, o conjunto dos números inteiros), se identifico qualquer número par, pela complementaridade, qualquer ímpar também pode ser identificado. A complementaridade baseia-se na dupla negação, o complementar do complementar de A é o próprio A. É o que Abe e Papavero (1991, p. 40) chamam de "versão conjuntista da lei da dupla negação".
O contraexemplo também é uma forma de negação, mas usado para mostrar que uma afirmação é falsa, visto que ele é um "exemplo" que contradiz uma definição ou uma regra apresentada. É o caso, por exemplo, da afirmação "p: todo o número primo é ímpar". Na tentativa de provar que essa afirmação é falsa, apresentamos o número 2 que é primo e par. Isto caracteriza um contraexemplo da afirmação p. Do ponto de vista lógico, podemos mostrar que uma afirmação é falsa provando que a sua negação é verdadeira.
Assim, a negação de que "p: todo o número primo é ímpar" é "~p: existe ao menos um número primo que não é impar". A afirmação ~p é verdadeira, o que leva a conclusão de que p é falsa.
Filho (1986) define o contra-exemplo na linguagem formal a partir de uma proposição e que surge quando precisamos mostrar que uma proposição é falsa. Para provar que a proposição p:  x ∈ A/p(x)2
2
"Qualquer elemento x pertencente ao conjunto A possui uma propriedade p(x)".
é falsa, basta mostrar que sua negação ~p: ∃ x ∈ A/~p(x)3
3
"Existe um elemento x pertencente a A que não possui a propriedade x".
é verdadeira, isto é, que existe ao menos um elemento x1∈ A que não verifica p(x), que torna p uma proposição falsa. Esse elemento x1 que caracteriza um contra-exemplo de p (falseia p) é um exemplo que verifica ~p.
x ∈ A/p(x)2
2
"Qualquer elemento x pertencente ao conjunto A possui uma propriedade p(x)".
é falsa, basta mostrar que sua negação ~p: ∃ x ∈ A/~p(x)3
3
"Existe um elemento x pertencente a A que não possui a propriedade x".
é verdadeira, isto é, que existe ao menos um elemento x1∈ A que não verifica p(x), que torna p uma proposição falsa. Esse elemento x1 que caracteriza um contra-exemplo de p (falseia p) é um exemplo que verifica ~p.
El Mekki (1991) reforça essa ideia afirmando que o contraexemplo surge nas demonstrações de teoremas ou, mesmo, na compreensão de definições em que o quantificador universal4 4 É um quantificador lógico, representando pelo símbolo , que se lê: "qualquer que seja" ou, ainda, "para todo". Um exemplo: ( x, x ∈ N), (qualquer que seja x, x pertence ao conjunto N) ou ainda (para todo x, x pertence ao conjunto N). se faz presente. A operação de negação exige a transformação do quantificador universal em quantificador existencial. Por exemplo, se queremos verificar se a proposição "todo elemento x pertencente a um conjunto A possui a propriedade p(x)" é verdadeira, basta verificar se, na sua negação, "existe algum elemento x pertencente ao conjunto A que não possui a propriedade p(x)". Esse elemento que "existe" e que não possui a propriedade p(x) é o contraexemplo da proposição p. O contraexemplo serve para demonstrar a falsidade de uma afirmação, ou seja, que uma propriedade não é verdadeira; para tal, é suficiente exibir que existe, pelo menos, um caso em que ela é falsa. Diz-se, então, que esse exemplo encontrado é o contraexemplo da afirmação. Para exemplificar, podemos questionar o valor-verdade da afirmação. Esta afirmação é falsa e apresentamos um contra-exemplo: para n = 3, temos 23 < 32 ou 8 < 9.
As formas de negação no processo de ensino: benefícios, equívocos, perigos
O contraexemplo é também muito usado para falsear concepções errôneas em relação a alguma definição ou resultado obtido. Nesse formato de uso comum, os contraexemplos excluem, de imediato, algumas dúvidas, permitem encaminhar os alunos à compreensão do objeto.
Podemos exemplificar uma situação encontrada no Sistema de Ensino Energia (2007b) para provar a falsidade da igualdade x.x = 2x. Imediatamente, o professor apresenta um contraexemplo: para x = 3 obtemos 3´3 ¹ 2´3. Portanto, não é verdade que x.x = 2x, pois existe um valor (x = 3) para o qual a proposição não se verifica, ou seja, para este valor, x.x ¹ 2x é verdadeira.
No processo de ensino, o contraexemplo é frequentemente utilizado de forma equivocada para apontar exemplos em que uma definição, propriedade ou teorema não se aplicam: o professor define "quadrilátero é um polígono que possui quatro lados" e, imediatamente, apresenta os "contraexemplos" de quadriláteros:
o o triângulo não é quadrilátero, porque não tem quatro lados, tem apenas três;
o um pentágono e um hexágono não são quadriláteros, pois possuem mais do que quatro lados.
A intenção, nesse caso, seria aproximar-se do que é quadrilátero, partindo do que não é quadrilátero. Contudo, se observarmos a afirmação "O quadrilátero é um polígono de quatro lados", podemos questionar se, de fato, há um contraexemplo para tal afirmação? A resposta a essa questão pode ser obtida utilizando-se a lógica:
Na linguagem formal, temos:
U = Conjunto de figuras planas convexas
Q = é quadrilátero
A afirmação q: (
Q ∈ U) (Q tem 4 lados)
A negação ~q: ( ∃ Q ∈ U) (Q não tem 4 lados).
Para acharmos um contraexemplo de q, temos de encontrar um exemplo que verifique ~q, ou seja, achar um quadrilátero no universo das figuras planas convexas que não tenha quatro lados, o que é impossível. Nesse caso, podemos perceber que a operação lógica que fundamenta esse raciocínio utilizado pelos professores é a contrapositiva: "Seja P polígono de U. Se P é um quadrilátero, então P tem quatro lados". Construindo a contrapositiva desta proposição podemos escrever que "P não tem quatro lados ⇒ P não é um quadrilátero". Os exemplos de não-quadriláteros usados pelo professor em sala de aula podem fundamentar-se, também, na noção de complementaridade, pois considerando o Conjunto U, formado pelos polígonos P convexos, temos os quadriláteros e os não-quadriláteros. Se excluirmos todos os não-quadriláteros do universo U, atingimos o conjunto dos quadriláteros. O uso desses exemplos na atividade matemática é muito comum e pode auxiliar na compreensão dos objetos em estudo.
No Sistema de Ensino Energia (2006) encontramos a seguinte fala do professor na explicação do conceito de função "[...] quando sair duas flechas de um mesmo elemento de A ou quando algum elemento de A não tiver flecha não é função. O resto todo é função. Basta vocês gravarem esses dois contra-exemplos para identificar quando é função ou não." Ele quer dizer que excluindo todos os casos de não-função, no universo das relações, o que resta é o conjunto das relações que são funções. Neste caso, são usados exemplos do que não interessa para caracterizar o que é função: "Basta vocês gravarem esses dois contra-exemplos [...]" (SISTEMA DE ENSINO ENERGIA, 2006), insiste o professor. Nesta situação, podemos observar o uso equivocado do termo contraexemplo no lugar de não-exemplo. A contrapositiva também pode ser caracterizada neste caso: "se f não tem tais características (sair duas flechas ou nenhuma de um mesmo elemento de A), então f não é função".
Este mesmo tipo de situação é encontrado em Di Pierro Netto e Orsi Filho (2000) que exemplificam um caso de confusão entre contraexemplo e não-exemplo. Esses autores apresentam exemplos de relações em diagramas que não são funções, ou seja, não-exemplos de funções como se fossem contraexemplos de funções. Aqui, como no caso anterior, podemos caracterizar o complementar: no universo das relações, há aquelas que são funções e as outras que não são funções.
Os usos dos não-exemplos, da contrapositiva e da negação, aliados à noção de conjunto complementar podem fornecer instrumentos importantes para o ensino da matemática, pois concorrem para uma ideia bastante simples, que é a de identificar "o que não é" para caracterizar "o que é".
É importante destacar que há noções que não são complementares: em relação ao universo da relações matemáticas, o conjunto das funções pares não é complementar ao conjunto das funções ímpares. Há função que não é par e nem ímpar, e há também aquela que é, ao mesmo tempo, par e ímpar. A função real f(x) = x3 + x2 + 1 não é nem par e nem ímpar, já a função que associa o zero ao zero (g(0) = 0) é par e ímpar (g(x) = g(-x) e g(x) = -g(-x)). Este é outro aspecto importante que deve ser destacado no ensino de matemática, a busca de elementos que tornam uma noção não complementar. No caso das funções pares e ímpares, podemos ver, mais uma vez, a importância da contrapositiva: seja f uma função com domínio simétrico e x0 qualquer elemento do domínio de f. Se f é par, então f(x0) = f(-x0).
A contrapositiva fica assim definida: se f(x0) ¹ (f(-x0), então f não é par. O uso da contrapositiva deixa claro que há muitos casos que tornam f(x0) ¹ (f(-x0), entre eles as funções ímpares f(x0) = - f(-x0). Mas, não são os únicos casos.
Dificuldades na aquisição da negação lógica
Uma das dificuldades que podem surgir na aprendizagem da noção de negação dos quantificadores universais é entender que essa negação não é somente própria da lógica matemática, mas também da língua natural. A questão é que a negação lógica dos quantificadores universais não coincide com aquela que se manifesta dentro da língua natural, o que gera grandes dificuldades na aquisição de tal noção.
Analisando a aplicação da negação, podemos pensar que, quando dizemos que "todos" possuem certa propriedade, isso significa dizer que todos, sem exceção, possuem tal propriedade. Mas quando dizemos "nem todos" possuem a propriedade, negamos o quantificador, e isso significa a perda da totalidade. Essa perda pode ocorrer por apenas um caso ou por vários. Quando afirmamos algo dizendo "todos" e surge um caso que quebra tal afirmação, esse caso é um contraexemplo para a afirmação.
Então, não ocorrer "todos" significa que "existe pelo menos um" caso que não se encaixa. As dificuldades surgem, pois, na linguagem formal, a negação de uma proposição com o quantificador universal transforma-se numa afirmação com o quantificador existencial:
(
x ∈ A p(x) (para todo x ∈ A possui a propriedade p(x));
~(
x ∈ A) p(x) ⇔ (∃ x ∈ A) ~p(x) (existe x ∈ A que não possui a propriedade p(x)).
Assim, vemos que a interação da negação com o quantificador universal "todo" é a origem de várias dificuldades. Um exemplo em Kilani (2002, p. 3) é o enunciado: "Todos os primeiros números naturais não são ímpares". Analisando a afirmação, podemos pensar, por exemplo, na sequência de números A = {1, 2, 3, 4, 5}, e verificarmos que é uma afirmação verdadeira, porque temos, em A, números pares e ímpares. Portanto, os primeiros números naturais "não são só ímpares". É importante salientar a diferença semântica entre "não são ímpares" e "são pares", apesar de serem expressões equivalentes. Quando substituímos "não são ímpares" por "são pares", temos o seguinte enunciado: "Todos os primeiros números naturais são pares". Essa troca conduz a um enunciado falso. A primeira afirmação significa que certos primeiros números naturais não são impares, o que dá a ela o estatuto de enunciado verdadeiro. Contudo, na troca das expressões, a afirmação nos conduz a outro sentido. Essa confusão é remarcada por Kilani (2002, p. 3):
A substituição de 'não são ímpares' por 'são pares' é legítima de um ponto de vista gramatical, visto que par e ímpar são antônimos um do outro e por consequência as expressões 'não são ímpares' e 'são pares' são sinônimos visto que dentro do conjunto dos números naturais um número é um número, seja par ou impar.
Observamos que, se usarmos as seguintes frases para a mesma situação, a questão pode se tornar mais compreensível: "nos primeiros números naturais, há números pares e há também números ímpares", que é verdadeira. Já a sua negação lógica "nos primeiros números naturais, todo número é par ou todo número é ímpar" é falsa, como era de se esperar.
Cerqueira e Oliva (1979) afirmam que a lógica e a matemática possuem uma propriedade comum, são linguagens e são formais, e têm as suas próprias regras de funcionamento, distinguindo-se do que chamamos de linguagem natural. São exemplos dessas diferenças, conforme pudemos constatar no exemplo anterior, o uso das proposições com conectivos "e" e "ou", e da negação dessas proposições nas linguagens natural e formal. É fato que a língua possibilita dois tipos de negação, e um deles coincide com a negação lógica e o outro não. Tudo isso permite prever a aparição de certas dificuldades por ocasião da manipulação das negações dos enunciados quantificados dentro da atividade matemática.
Um exemplo bastante revelador, que mostra a concepção equivocada na atividade matemática de negar "todos" por "nenhum", é o aplicado por Kilani (2002) em sua pesquisa com alunos do ensino secundário: Seja a definição seguinte de uma função derivável sobre o conjunto dos reais ℜ: Uma função f é derivável sobre ℜ se é derivável em qualquer (ou todos) ponto de ℜ. Dê o enunciado que corresponde à definição de uma função não-derivável sobre ℜ e justifique a sua resposta. Este autor verificou que 58% dos alunos formularam respostas corretas, porém 40% deles apresentaram respostas do tipo: "Uma função f não é derivável em ℜ, se ela não é derivável em nenhum ponto de ℜ".
Duval (1995) apresenta o Quadro 3, que mostra a diferença da negação usada nas linguagens natural e formal.
Neste quadro, podemos observar as diferentes formas ligadas aos tipos de negação nas linguagens natural e formal. Sobre o tema das funções injetoras tratado anteriormente, observamos, em Sistema de Ensino Energia (2007a), o uso da negação por comutação extensional, quando considera o gráfico de funções para explicar como reconhecer as funções injetoras: "A função será injetora se todas as linhas paralelas ao eixo Ox interceptam a curva em, no máximo, um ponto. Não será injetora se algumas linhas paralelas ao eixo Ox interceptam o gráfico em mais de um ponto" (SISTEMA DE ENSINO ENERGIA, 2007a). Na sequência, ele usa a dupla negação para chamar atenção dos alunos em um gráfico apresentado; "olhem o gráfico... ele é injetor porque não existe nenhuma linha que corta a função em mais de um ponto! Todas cortam em apenas um ponto" (SISTEMA DE ENSINO ENERGIA, 2007a).
Duval (1988) assinala que na verificação de afirmações em que é empregada a negação possui um maior custo cognitivo. Se um questionamento é feito na forma negativa, ele pode ser reexaminado por meio de um caso positivo em detrimento do caso negativo. Observamos este procedimento na fala do professor em Sistema de Ensino Energia (2007b), no exercício seguinte: Dado o conjunto A = {1, 2, {3}, 4}, qual é o valor verdade de {1} É A. O professor explica: "Olha essa frase.... Pensa bem.... Verdadeiro ou falso? Olha que a negação pode te atrapalhar! Vou te dar uma dica: Vou apagar a negação.... leia agora....{1} É A. Me responde... {1} é conjunto de A? Verdadeiro ou falso? Falso! Então, se assim: {1}É A fica falso é porque assim: {1}É A fica verdadeiro! É lógico! Claro! Se você se atrapalha com a negação, pensa o contrário e daí marca o contrário" (Sistema de Ensino Energia, 2007b).
Em outras situações, o professor enuncia as suas próprias regras em linguagem natural de forma equivocada ou incompleta, com objetivo de contornar ou, mesmo, evitar o formalismo matemático. A utilização dessas regras pode surtir o efeito desejado, mas mostra-se apenas delineada para um tipo de tratamento a ser realizado. Por exemplo, para identificar se um gráfico é de uma função ou não, o professor estabelece a regra, como, por exemplo, a situação encontrada em Sistema de Ensino Energia (2007b) no estudo da definição de função: "para ser função, todas as linhas verticais não podem cortar em mais de um ponto o gráfico", esquecendo-se também que, para ser função, cada linha vertical, no domínio da função, deve cortar em algum ponto do gráfico.
Considerações finais
Franco (2008) constata que é bastante frequente, na prática do professor do Ensino Médio, o uso das formas de negação: "Percebemos em alguns tópicos de matemática que o professor usa as formas de negação como uma técnica de ensino no momento que faz a sua leitura do conteúdo a ser ministrado e elabora outra forma de apresentá-lo". (FRANCO, 2008, p. 130, grifo do autor)
O conceito de complementariedade é muito utilizado nas aulas; o professor apresenta os casos que não se aplicam, por exemplo, a uma definição com o objetivo de atingir o objeto pretendido pela complementariedade. Essa prática acontece, na maioria dos casos, entrelaçada à dupla negação. O professor expõe um universo bem determinado e, a partir da negação, mostra os casos que não se enquadram na definição; e, negando-os, ele retorna ao objeto pretendido a partir da invariabilidade da referência que é determinada pela dupla-negação.
Apontamos, neste estudo, dificuldades que surgem na negação de proposições com a presença de quantificadores universais. Há diferenças importantes entre a negação dessas proposições, quer estejamos utilizando a linguagem formal ou a linguagem comum. A negação de uma proposição apresentada por meio da linguagem formal com o quantificador universal transforma-se em uma afirmação com o quantificador existencial, mas, na linguagem comum, isso não acontece sempre. Não ocorrer "todos" significa que "existe pelo menos um". Na linguagem comum, é trivial negar "todos" por "nenhum", no lugar de negar "todos" por "existe um" ou "algum".
O presente estudo indica um aumento de registros de representações a partir do uso das formas de negação, o que dá, ao professor, maiores possibilidades no desenvolvimento do seu trabalho em sala de aula. As possibilidade de apreensão de um objeto matemático são potencializadas pelo aumento do número de registros desse objeto: um único registro não permite, em geral, a apreensão do objeto em sua totalidade. Duval (1995) centra sua hipótese de aprendizagem não apenas no conhecimento de registros de um mesmo objeto, mas sobretudo nas transformações entre esses registros. Quanto mais registros de um mesmo objeto, maiores as possibilidades de sua apreensão por conta do aumento do número de operações possíveis entre eles.
Baseando-nos no esquema de hipótese fundamental de aprendizagem de Duval (1995) construímos um esquema semelhante, em que as formas de negação indicadas por A' e B' podem ser utilizadas (Figura 4).
Esse esquema apresenta dois registros de representação A e B e as transformações externas de conversões entre eles, mas, diferentemente da Figura 1, sugere um tratamento que utiliza a negação e formas de negação. Destaca, também, a conversão "diagonalmente" entre o registro A e o registro B', e vice-versa; a conversão entre o registro B e A', e vice-versa, que indicam possibilidades de permuta de posição entre esses registros.
Constatamos, no exemplo representado na Figura 4, que a afirmação na forma negativa pode ser utilizada pelo professor como o Registro A, quer dizer, ele pode começar a explicação pela negação, mostrando o que não pode ser, para, depois, passar para a forma positiva A' (linguagem natural) e, em seguida, para o registro B' (linguagem formal). No exemplo da figura 4, "x não pode ser nulo" por conta da divisão por x e "x não pode ser negativo" por conta da raiz quadrada de x no numerador da expressão. Temos, então, que "x não é nulo e x não é negativo", o que equivale dizer que "x é positivo" ou "x > 0". Observamos nessas transformações:
o tratamento para a passagem de "x não é nulo e x não é negativo" para "x é positivo", que pode requerer uma representação intermediária com retas reais, por exemplo;
o conversão na passagem de "x é positivo" para "x > 0".
Essas duas operações podem exigir "uma comparação dos tratamentos por negação [que] é essencial para uma coordenação de registros" conforme assinala Duval (1995, p. 164).
Este é um exemplo bem simples e mostra que o uso das formas de negação pode possibilitar a construção e o emprego de diferentes registros de representação e fornecer instrumentos importantes para o ensino da Matemática. O esquema da hipótese fundamental de aprendizagem de Duval (1993) fica enriquecido com esta contribuição do uso das formas negativas. Constatamos, na negação e nas formas de negação, elementos importantes para a prática do professor, consideradas a superação das lacunas existentes em relação ao conhecimento da lógica formal e, sobretudo, das implicações, dificuldades e diferenças que ocorrem na negação de representações nas linguagens natural e formal. "Ainda que a língua formal possa cumprir as mesmas funções discursivas que uma língua natural, sua estrutura não apresenta nenhuma semelhança com ela" (DUVAL, 1995, p. 137).
As formas de negação estão vivas na sala de aula, fornecem instrumentos importantes para a aprendizagem matemática, pois possibilitam a criação de novos registros e a transformação desses registros tão caros à aprendizagem matemática.
Artigo recebido em 21/06/2011.
Aceito em 18/01/2012.
- ABE, J. M.; PAPAVERO, N. Teoria intuitiva dos conjuntos São Paulo: Makron, 1991.
- BARNETT, R. Teoria e problemas de geometria 3. ed. São Paulo: Bookman, 2003.
- CERQUEIRA, L. A.; OLIVA, A. Introdução à lógica Rio de Janeiro: Zahar, 1979.
- DI PIERRO NETTO, S.; ORSI FILHO, S. Matemática em fascículos para o ensino médio São Paulo: Saraiva, 2000.
- DUCROT, O. Princípios de semântica lingüística São Paulo: Cultrix, 1972.
- DUVAL, R. Ecarts sémantiques et cohérence mathématique: introduction aux problèmes de congruence. Annales de Didactique et de Sciences Cognitives, Strasbourg, v. 1, p. 7-26, 1988.
- ______. Registres de représentation sémiotique et fonctionnement cognitif de la pensé. Annales de Didactique et de Sciences Cognitives, Strasbourg, v. 5, p. 37-65, 1993.
- ______. Sémiosis et pensée humaine: registres sémiotiques et apprentissages intellectuels. Bern: Peter Lang, 1995.
- ______. Quel cognitif retenir en didactique des mathématiques? Recherches en Didactique des Mathématiques, Grenoble, v. 16, n. 3, p. 349-382, 1996.
- ______. Registros de representações semióticas e funcionamento cognitivo da compreensão em matemática. In: MACHADO, S. D. de A. (Org.). Aprendizagem em matemática: registros de representação semiótica. Campinas: Papirus, 2003. p. 11-34.
- EL MEKKI, EL F. Logique et enseignement mathématique: document à l'attention des professeurs de mathématique. Strasbourg: Institut de Recherche sur l'Enseignement des Mathematiques, 1991. v. 3. p. 22-25.
- FILHO, E. A. Iniciação à lógica matemática. São Paulo: Nobel, 1986.
- FRANCO, P. L. Estudo de formas de negação no ensino de matemática: ponto de encontro com os registros de representação semiótica. 2008. 142 f. Dissertação (Mestrado em Educação Científica e Tecnológica) Universidade Federal de Santa Catarina, Florianópolis, 2008.
- KILANI, B. I. D. La négation grammaticale dês énoncés universellement quantifiés risque t-elle d'être un obstacle a l'acquisition de la négation logique? Grenoble: La Penseé Sauvage, 2002. p. 1-8. 1 CD.
- MORETTI, M. T. O papel dos registros de representação na aprendizagem da matemática. Contrapontos, Itajaí, v. 2, n. 6, p. 343-363, 2002.
- SAUSSURE, F. Curso de linguística geral 30. ed. São Paulo: Cultrix, 2008.
- SISTEMA DE ENSINO ENERGIA. Apostilas de matemática do ensino médio: curso terceirão. Florianópolis: Energia, 2007a.
- ______. Material didático ensino médio, curso terceirão: MTM A. Itajaí: Energia, 2007b. 1 CD-ROM.
- ______. Material didático ensino médio, curso terceirão: MTM A. Brusque: Energia, 2006. 1 CD-ROM.
 , que se lê: "qualquer que seja" ou, ainda, "para todo". Um exemplo: (
, que se lê: "qualquer que seja" ou, ainda, "para todo". Um exemplo: (  x, x ∈ N), (qualquer que seja x, x pertence ao conjunto N) ou ainda (para todo x, x pertence ao conjunto N).
x, x ∈ N), (qualquer que seja x, x pertence ao conjunto N) ou ainda (para todo x, x pertence ao conjunto N).Datas de Publicação
-
Publicação nesta coleção
14 Jun 2012 -
Data do Fascículo
2012
Histórico
-
Recebido
21 Jun 2011 -
Aceito
18 Jan 2012