ABSTRACT:
The Nitrogen content of rice leaves has a significant effect on growth quality and crop yield. We proposed and demonstrated a non-invasive method for the quantitative inversion of rice nitrogen content based on hyperspectral remote sensing data collected by an unmanned aerial vehicle (UAV). Rice canopy albedo images were acquired by a hyperspectral imager onboard an M600-UAV platform. The radiation calibration method was then used to process these data and the reflectance of canopy leaves was acquired. Experimental validation was conducted using the rice field of Shenyang Agricultural University, which was classified into 4 fertilizer levels: zero nitrogen, low nitrogen, normal nitrogen, and high nitrogen. Gaussian process regression (GPR) was then used to train the inversion algorithm to identify specific spectral bands with the highest contribution. This led to a reduction in noise and a higher inversion accuracy. Principal component analysis (PCA) was also used for dimensionality reduction, thereby reducing redundant information and significantly increasing efficiency. A comparison with ground truth measurements demonstrated that the proposed technique was successful in establishing a nitrogen inversion model, the accuracy of which was quantified using a linear fit (R2=0.8525) and the root mean square error (RMSE=0.9507). These results support the use of GPR and provide a theoretical basis for the inversion of rice nitrogen by UAV hyperspectral remote sensing.
Key words:
UAV; Hyperspectral remote sensing; Machine learning; Nitrogen content
RESUMO:
O teor de nitrogênio das folhas de arroz tem um efeito significativo sobre a qualidade do crescimento e o rendimento das culturas. Propõe-se e demonstrou-se um método não invasivo para a inversão quantitativa do teor de nitrogênio do arroz com base em dados de detecção remota hiperespectral coletados por um veículo aéreo não tripulado (UAV). As imagens de albedo do dossel de arroz foram adquiridas por uma imagem de imagem hiperespectral a bordo de uma plataforma M600-UAV. O método de calibração da radiação foi então usado para processar esses dados e a reflectância das folhas do dossel foi adquirida. A validação experimental foi realizada utilizando o campo de arroz da Universidade Agrícola de Shenyang, que foi classificado em 4 níveis de fertilizantes: nitrogênio zero, baixo teor de nitrogênio, nitrogênio normal e alto teor de nitrogênio. A regressão do processo gaussiano (GPR) foi então usada para treinar o algoritmo de inversão para identificar bandas espectrais específicas com a maior contribuição. Isso levou a uma redução no ruído e uma maior precisão de inversão. A análise de componentes praincipais (PCA) também foi usada para redução de dimensionalidade, reduzindo assim a informação redundante e aumentando significativamente a eficiência. Uma comparação com as medidas de verdade no solo demonstrou que a técnica proposta foi bem sucedida no estabelecimento de um modelo de inversão de nitrogênio, cuja precisão foi quantificada usando um ajuste linear (R2 = 0,8525) e o erro quadrático médio quadrado (RMSE = 0,9507). Estes resultados suportam o uso do GPR e fornecem uma base teórica para a inversão do nitrogênio do arroz pela detecção remota hiperespectral do UAV.
Palavras-chave:
UAV; detecção remota hiperspectral; aprendizado de máquinas; conteúdo de nitrogênio
INTRODUCTION:
Nitrogen is the primary component of rice protein and chlorophyll, which is critical for crop growth and yield (LEE et al. (2008LEE, Y.J. et al. A simple spectral index using reflectance of 735nm to assess nitrogen status of rice canopy. Agronomy Journal, v.100, p.205-212, 2008. Available from: https://dl.sciencesocieties.org/publications/aj/abstracts/100/1/205>. Accessed: Jan. 13, 2017. doi:10.2134/agronj2007.0018.
https://dl.sciencesocieties.org/publicat...
); WANG et al. (2011WANG, J.N. et al. Effects of N, P, K Fertilizer application on grain yield, quality, nutrient uptake and utilization of rice. Chinese Journal of Rice Science, v.6, p.645-653, 2011. Available from: http://en.cnki.com.cn/Article_en/CJFDTotal-ZGSK201106013.htm>. Accessed: Nov. 25, 2017. doi:10.3969/j.issn.1001-7216.2011.06.012.
http://en.cnki.com.cn/Article_en/CJFDTot...
)). Liaoning province in northeast China is currently facing three issues with the application of nitrogen fertilizer. Fertilizer nitrogen levels per hectare are high, fertilization is not balanced, and the utilization rate of nitrogen fertilizer is low. Excessive and unguided application of nitrogen fertilizer increases production costs, causes environmental pollution (WANG et al. (2014WANG, P., LUO, X.W. Key technology for remote sensing information acquisition based on micro UAV. Transactions of the Chinese Society of Agricultural Engineering, v.18, p.1-12, 2014. Available from: http://www.ingentaconnect.com/content/tcsae/tcsae/2014/00000030/000000.18/art00001#>. Accessed: Jun. 12, 2016. doi: 10.3969/j.issn.1002-6819.2014.18.001.
http://www.ingentaconnect.com/content/tc...
); DU et al. (2017DU, W., XU, T.Y. Effect and assessment of UAV spraying parameters at japonica rice canopies. Journal of Agricultural Mechanization Research, v.4, p.182-186, 2017. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=njhyj201704036>. Accessed: May. 03, 2016. doi: 10.3969/j.issn.1003-188X.2017.04.036.
http://www.wanfangdata.com.cn/details/de...
)), and results in erratic and unstable stem growth (YU & XU, 2016YU, F.H., XU, T.Y. Models for estimating the leaf NDVI of japonica rice on a canopy scale by combining canopy NDVI and multisource environmental data in Northeast China. International Journal of Agricultural and Biology, v.9, p.132-142, 2016. Available from: https://ijabe.org/index.php/ijabe/article/view/2266>. Accessed: Feb. 09, 2017. doi:10.3965/j.ijabe.20160905.2266.
https://ijabe.org/index.php/ijabe/articl...
). Conventional nitrogen content detection requires destructive sampling in the field and subsequent laboratory testing, which cannot be conducted in real time. More efficient methods for the detection of nitrogen content in rice are needed to meet future requirements for crop production and environmental sustainability (LAN, 2013LAN, Y.B. Agricultural aviation applications in USA. Transactions of the Chinese Society for Agricultural Machinery, v.5, p.194-201, 2013. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=nyjxxb201305034>. Accessed: Apr. 14, 2017. doi:10.6041/j.issn.1000-1298.2013.05.034.
http://www.wanfangdata.com.cn/details/de...
).
Remote sensing techniques have offered a non-invasive alternative to conventional crop sampling over large areas and are becoming ever more indispensable in plant nutrient research and precision agriculture (LI et al. (2016LI, M. et al. A systematic comparison of different object-based classification techniques using high spatial resolution imagery in agricultural environments. International Journal of Applied Earth Observation and Geoinformation, v.49, p.87-98, 2016. Available from: http://agri.ckcest.cn/ass/NK005-20160328004.pdf>. Accessed: Mar. 24, 2016. doi: 10.1016/j.jag.2016.01.011.
http://agri.ckcest.cn/ass/NK005-20160328...
); MULLA et al. (2013MULLA, D.J. Twenty-five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosystems engineering, v.114, p.358-371, 2013. Available from: http://ccc.inaoep.mx/~mdprl/documentos/17062015.pdf>. Accessed: May. 20, 2016. Doi:10.1016/j.jag.2016.01.011.
http://ccc.inaoep.mx/~mdprl/documentos/1...
)). Data from airborne imaging systems have been used for the calculation and retrieval of biophysical parameters such as chlorophyll content (VERRESLST et al. (2013)), leaf area index (LAI) (GARRIGUES et al. (2008GARRIGUES, S. et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. Journal of Geophysical Research: Biogeosciences, v.113, 2008. Available from: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2007JG000635> . Accessed: Jul. 13, 2017. doi:10.1029/2007JG000635.
https://agupubs.onlinelibrary.wiley.com/...
)), and fractional vegetation cover (VERRELST et al. (2012VERRELST, J. et al. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Transactions on Geoscience and Remote Sensing, v.50, p.1832-1843, 2012. Available from: https://www.mendeley.com/research-papers/retrieval-vegetation-biophysical-parameters-using-gaussian-process-techniques/>. Accessed: Nov. 18, 2016. doi:10.1109/TGRS.2011.2168962.
https://www.mendeley.com/research-papers...
)). Use of unmanned aerial vehicles (UAVs) has provided a low-cost option for the acquisition of such data. This approach has several advantages including flexibility in the choice of flight altitude, detection range, spectral resolution, and sensor type. The equipment is fast and easy to transport, allowing for timely deployment at specific crop life stages.
The UAV-based imaging systems have recently been used for multiple aspects of vegetation monitoring (SUGIURA et al. (2005SUGIURA, R. et al. Remote-sensing technology for vegetation monitoring using an unmanned helicopter. Biosystems Engineering , v.90, p.369-379, 2005. Available from: http://elibrary.asabe.org/abstract.asp?aid=17837>. Accessed: Sep. 15, 2017. doi: 10.13031/2013.1 7837.
http://elibrary.asabe.org/abstract.asp?a...
); LIU, 2014LIU, F. Study on monitoring fractional vegetation cover of garden plots by unmanned aerial vehicles. Transactions of the Chinese Society for Agriculural Machinery, v.45, p.250-257, 2014. Available from: http://www.wanfangdata.com.cn/details/detail.d o?_type=perio&id=nyjxxb201411039>. Accessed: Dec. 11, 2017. doi:10.6041/j.issn.1000-1298.2014.11.039.
http://www.wanfangdata.com.cn/details/de...
), including the fast acquisition of canopy reflectance data from crops (WATTS et al. (2012WATTS, A.C. et al. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sensing, v.4, p.1671-1692, 2012. Available from: http://www.mdpi.com/2072-4292/4/6/1671>. Accessed: Jul. 14, 2017. doi:10.3390/rs4061671.
http://www.mdpi.com/2072-4292/4/6/1671...
); COLOMINA & MOLINA, 2014COLOMINA, I., MOLINA, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS Journal of Photogrammetry and Remote Sensing, v.92, p.79-97, 2014. Available from: https://zenodo.org/record/57983#.WyO_o0xuJPY>. Accessed: Sep. 17, 2016. doi:10.1016/j.isprsjprs.2014.02.013.
https://zenodo.org/record/57983#.WyO_o0x...
). For example, the nondestructive evaluation of onion canopies led to the establishment of a direct relationship between canopy density and LAI (CÓRCOLES et al., 2013CÓRCOLES, J.I. et al. Estimation of leaf area index in onion (Allium cepa L.) using an unmanned aerial vehicle. Biosystems Engineering, v.115, p.31-42, 2013. Available from: https://www.sciencedirect.com/science/article/pii/S1537511013000214?via%3Dihub>. Accessed: Mar. 7, 2017. doi:10.1016/j.biosystemseng.2013.02.002.
https://www.sciencedirect.com/science/ar...
). Acquisition of hyperspectral images has allowed for the expansion and diversification of crop measurements, to include parameters such as yield, biomass, and water content (ADAM et al. (2010ADAM, E. et al. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: a review. Wetlands Ecology and Management, v.18, p.281-296, 2010. Available from: https://link.springer.com/article/10.100 7%2Fs11273-009-9169-z>. Accessed: Jun. 27, 2017. doi:10.1007/s11273-009-9169-z.
https://link.springer.com/article/10.100...
); GOVENDER et al. (2007GOVENDER, M. et al. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa, v.33, p.145-151, 2007. Available from: http://www.oalib.com/paper/1350213#.WyPCUUxuJPY>. Accessed: Jan. 12, 2016. doi:10.4314/wsa.v33i2.49049.
http://www.oalib.com/paper/1350213#.WyPC...
)). Spectroscopy data have also been used for phenol typing (ZAMAN-ALLAH et al. (2015ZAMAN-ALLAH, M. et al. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant methods, v.11, p.35, 2015. Available from: https://plantmethods.biomedcentral.com/articles/10.1186/s13007-015-0078-2>. Accessed: Feb. 18, 2016. doi:10.1186/s13007-015-0078-2.
https://plantmethods.biomedcentral.com/a...
); SANKARAN et al. (2015SANKARAN, S. et al. Field-based crop phenotyping: Multispectral aerial imaging for evaluation of winter wheat emergence and spring stand. Computers and Electronics in Agriculture, v.118, p.372-379, 2015. Available from: https://www.sciencedirect. com/science/article/pii/S0168169915002768>. Accessed: May. 15, 2017, doi:10.1016/j.compag.2 015.09.001.
https://www.sciencedirect. com/science/a...
)), and quantification of structural and biochemical vegetation properties. (SCHAEPMAN et al. (2009SCHAEPMAN, M. E. et al. Earth system science related imaging spectroscopy-an assessment. Remote Sens. Environ, v.113, p.123-137, 2009. Available from: https://www.sciencedirect.com/science/article/pii/S0034425709000819>. Accessed: Mar. 02, 2017, doi:10.1016/j.rse.2009.03.001.
https://www.sciencedirect.com/science/ar...
); USTIN & GAMON, 2010USTIN, S., GAMON, J. Remote sensing of plant functional types. New Phytologist, v.186, p.795-816, 2010. Available from: https://www.ncbi.nlm.nih.gov/pubmed/20569415>. Accessed: Apr. 22, 2016. doi:10.1111/j.1469-8137.2010.03284.x.
https://www.ncbi.nlm.nih.gov/pubmed/2056...
; HOMOLAVÁ et al. (2013HOMOLOVÁ, L. et al. Review of optical-based remote sensing for plant trait mapping. Ecological Complexity, v.15, p.1-16, 2013. Available from: http://library.wur.nl/WebQuery/wurpubs/442967>. Accessed: May. 15, 2017. doi:10.1016/j.ecocom.2013.06.003.
http://library.wur.nl/WebQuery/wurpubs/4...
)).
However, this technology poses an important methodological challenge. Imaging spectroscopy data typically included highly correlated and noisy spectral bands, which frequently cause statistical problems due to small sample sizes. In this study we demonstrated the application of Gaussian process regression (GPR) to overcome these limitations. GPR is a type of machine learning algorithm capable of being trained to differentiate the contributions of various spectral bands. Bands with the highest weight (contribution to a specific parameter being measured) are selected while other less relevant bands are ignored. This leads to a reduction in noise and increased parameter measurement accuracy. The application of GPR is specifically demonstrated for the inversion of nitrogen content in rice crops.
The remainder of this paper is organized as follows. Methods section described the process of image acquisition, processing, and the establishment of a nitrogen content ground truth by invasive field sampling. Data processing and GPR algorithm are also explained in addition to the dimensionality reduction achieved using principal component analysis (PCA). This procedure was used to remove redundant information in the hyperspectral data, significantly increasing the efficiency of the proposed technique. Retrieved nitrogen content is then compared with the ground truth in results section and quantified using the root-mean-square-error (RMSE) as well as a linear fit. Discussion then provides a rationale for the choice of GPR and a comparison between this and other UAV-based hyperspectral imaging studies. Comparisons are made and benefits of this proposed technique as a novel imaging tool for crop monitoring are presented, plans for future studies are discussed, and the paper is concluded.
MATERIALS AND METHODS:
The study site was located at Shenyang Agricultural University (41°81′63″N, 123°55′85″E; altitude 65 m) in Shenyang, Liaoning Province, China (see Fig.1). The tested rice-529 cultivar were provided by the College of Agriculture at Shenyang Agricultural University. Rice plant spacing was ~30cm, with a growth period of ~149 days. Stalks were transplanted on May 29, 2016. Seedlings were an early-maturing variety with dark green leaves, reaching a full height of ~107cm. A total of 12 plots (5m×8m) were established, consisting of four nitrogen (N) treatments with three replicates in a randomized block design (see Figure 1). Subgroups were arranged as follows:
(1) 0 level (in 2016) designated as no nitrogen.
(2) 1 level = 2 level×0.5 (in 2016) designated as low nitrogen.
(3) 2 level (N: 0.2kg/ha, P: 0.23kg/ha, K:0.08kg/ha) (in 2016) designated as normal nitrogen.
(4) 3 level = 2 level×1.5 (in 2016) designated as high nitrogen.
A plastic plate isolation test plot was used, in which soil was inserted into a 10cm chamber to ensure fertilizer did not penetrate other plots.
UAV hyperspectral image acquisition
A six-rotor UAV (M600, DJI, China) was used for hyperspectral image acquisition. The device was capable of lifting 6.5kg with a flight time of ~20 minutes. The UAV was equipped with an attitude control system (RONIN-MX, DJI, China) to eliminate vibrations effects in the spectral image acquisition process. The Gaiasky-mini imager (Dualix Spectral Imaging, China) was used to collect top-of-rice hyperspectral reflectance data ranging from 400 to 1100nm with a 3.0nm resolution (256 bands), from an altitude of 50m. The data acquisition time was consistently between 12:00 and 10:00 to ensure acquisition under the same sky conditions.
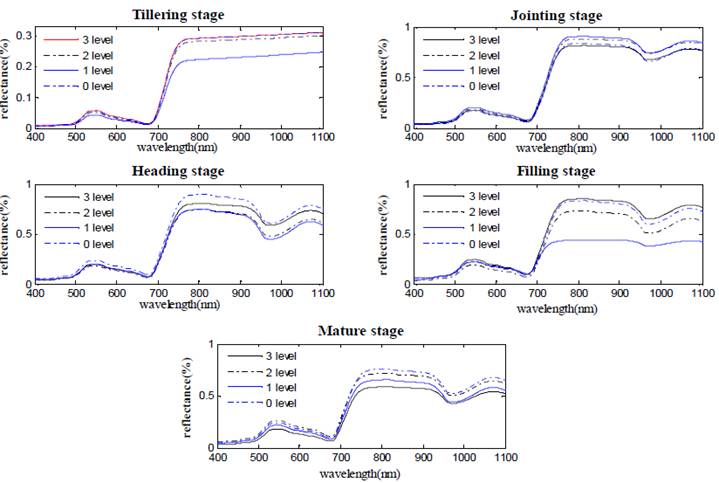
Rice canopy spectral information was collected by a black and white calibration board and the digital number (DN) was converted to a reflectance. The experiment was conducted in the tilling, jointing, heading, filling, and maturity stages of rice. Spectral curves for the five rice growth stages and four nitrogen levels are presented in figure 2. As is evident in the figure, the reflectance of various nitrogen levels was smaller in the visible light band (400-720nm) and larger in the near-infrared (NIR) region (800-980nm). The NIR reflectance was significantly different in the heading, filling, and mature stages. The other fields were all consistent in the same growth stage, except for varying nitrogen levels. These variations in the NIR band could be used to non-invasively measure nitrogen levels in rice.
Nitrogen measurements in rice
The acquisition of nitrogen levels from hyperspectral data requires knowledge of the growth conditions for each plant. As such, artificial destructive sampling was used to measure the nitrogen content of each plot and provide a ground truth for validating the nitrogen model. Nitrogen content of the rice was obtained by Kjeldahl determination (AN et al. (2004AN, G. A. et al. Studies on the detemination of ammonia-nitrogen in water samples by BUCHI Kjeldahl line instrument. Modern Scientific Instruments, v.1, p.28-29, 2004. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xdkxyq200401010>. Accessed: May. 27, 2017. doi:10.3969/j.issn.1003-8892.2004.01.010.
http://www.wanfangdata.com.cn/details/de...
); SEVERTSON et al. (2016SEVERTSON, D. et al. Unmanned aerial vehicle canopy reflectance data detects potassium deficiency and green peach aphid susceptibility in canola. Precision Agriculture, p.1-19 2016. Available from: https://link.springer.com/article/10.1007%2Fs11119-016-9442-0>. Accessed: Jul. 20, 2016 doi:10.1007/s11119-016-9442-0.
https://link.springer.com/article/10.100...
)). A sample of 3-5 crops were selected from each cell and the fresh leaves were placed in an oven at 105°C for 15 minutes, dried at 70°C, and then crushed. After heating, samples were distilled and titrated. Nitrogen content was calculated as follows:
…(1)
where V (mL) and V 0 (mL) are the volumes of the acid standard solution used to titrate the test solution and the acid standard solution used for blank titration, respectively. The terms (mol/L) and m are the acid standard solution concentration and dry sample quality, respectively.
Hyperspectral Data Processing
In addition to rice plant data, this hyperspectral imaging method collects information on the soil and water as well. The spectral angle mapper (SAM) method was used in this study to classify hyperspectral images and obtain pure rice information. This was done using the ENVI 5.3 software package (Harris Geospatial Solutions, Broomfield, CO, USA) and an n-dimensional angle to match pixels in the reference spectrum. The algorithm implemented a spectrum of N bands as an N-dimensional spectral vector. The similarity between any two spectra was determined by calculating the angle between the N-dimensional vector and the endmember spectrum, with smaller angles representing higher similarity. In this study, raw data from 50 regions of interest (ROIs) were selected from the hyperspectral remote sensing images. The maximum angle threshold was set to 0.1 (radians) for all classifications, indicating that if the angle between the pixel spectrum and endmember spectrum was less than 0.1, they were subdivided into a single class.
Dimensionality reduction
Image-based canopy reflectance data were acquired using cameras which access multispectral (2-10) or hyperspectral (>10) radiation bands in the visible and near-infrared spectra. These properties may lead to a violation of basic assumptions underlying statistical models or may otherwise bias the outcome. Models fitted with such multi-collinear data are prone to over-fitting, limiting the applicability of these results to other scenarios. These issues affect prediction accuracy as well as the interpretability of regression (retrieval) models. As such, it is beneficial to reduce the spectral dimension, either through reduction techniques or selection of particular spectral regions which are most applicable to targeted biophysical variables.
Principal component analysis (PCA) (CHEN & QIAN, 2011CHEN, G.Y., QIAN, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Transactions on Geoscience and Remote Sensing, v.49, p.973-980, 2011. Available from: https://ieeexplore.ieee.org/document/5607305/>. Accessed: Jun. 10, 2017. doi:10.1109/TGRS.2010.2075937.
https://ieeexplore.ieee.org/document/560...
; JOLLIFFE, 2002JOLLIFFE, I.T. Principal Component Analysis. Second Edition, New York: Springer, p.1-6, 2002.) was used to improve operational efficiency and reduce data dimensionality. In this process, an orthogonal transformation was utilized to transform the original correlated random vectors into new uncorrelated vectors (SHLENS, 2002SHLENS, J. A tutorial on principal component analysis. New York: Cornell University, 2002.), thereby decomposing the eigenvalues of the covariance matrix using the Kullback-Leibler approach (ZENG et al. (2013ZENG, L. et al. Compressed sensing based speech spare representation with KL expansion. Journal of Data Acquisition and Processing, v.3, p.267-273, 2013. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjcjycl201303002>. Accessed: Nov. 19, 2017. doi:10.3969/j.issn.1004-9037.2013.03.002.
http://www.wanfangdata.com.cn/details/de...
). The feature vector corresponds to the principal component of the data and the eigenvalue corresponds to the weight of each principal component. Each base vector is independent of the other components and each component can be studied separately. The degree of influence can be determined from the corresponding eigenvalues, as smaller eigenvalues indicate less influence. The principal component was selected and the dimension reduced using singular value decomposition (SVD) (ZHAO et al. (2015ZHAO, F. et al. An image algorithm based on singular value decomposition. Journal of Computer Research and Development, v.47, p.23-32, 2015. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyjyfz201001004>. Accessed: Dec. 23, 2016.
http://www.wanfangdata.com.cn/details/de...
)).
In this study, we first collected the initial hyperspectral data and calculated the correlation coefficient matrix. The covariance matrix R, established from the normalized correlation data matrix, reflects the degree of correlation, as higher values are indicative of improved principal component analysis. Among these values, R ij (i, j = 1, 2, …, p) is the correlation coefficient for the original hyperspectral information X i and X j . It is worth noting that R is a real symmetric matrix, that is R ij = R ji . As such, it is only necessary to calculate either the upper or lower triangular elements as follows:
…(2)
The number of principal components was determined by calculating the eigenvalues of the covariance matrix R, the principal component contribution rate, and the cumulative variance contribution rate. Solutions of the characteristic equation | λE -R|=0 were used to calculate the eigenvalues λi (i, j = 1, 2, …, p) in ascending order of size (λ1 ≥ λ2 ≥ … ≥ λi ≥ 0). These eigenvalues are the variance (influence) of each principal component. The contribution of a given principal component Z i is given by:
…(3)
The cumulative contribution rate can then be expressed as:
…(4)
Eigenvalue criteria were used to select principal components, which were required to be larger than 1 with a cumulative contribution rate of 80-95%. The A values corresponded to main components of 1, 2, and M (m, P), where m is the number of principal components. Characteristic values λ1, λ2, …, λm corresponded to principal components 1, 2, …, m (m ≤ p). The initial factor load matrix was established, in addition to the correlation coefficient R (Z i , X i ) of the principal component Z i and original index X i . The significance of principal components is demonstrated by their correlation with hyperspectral information.
Gaussian Process Regression
Gaussian process regression (GPR) is a nonparametric black box model (TAERYON, 2007TAERYON, C. Alternative posterior consistency results in nonparametric binaryregression using Gaussian process priors. Journal of Statistical Planning and Inference, v.137, p.2975-2983, 2007. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0378375807000407>. Accessed: Sep. 26, 2017. doi:10.1016/j.jspi.2006.11.001.
https://linkinghub.elsevier.com/retrieve...
)equivalent to kernel ridge regression or kriging (VERRELST et al. (2016VERRELST, J. et al. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. International Journal of Applied Earth Observation and Geoinformation, v.52, p.554-567, 2016. Available from: http://ipl.uv.es/artmo/files/Verrelst_etal2016_GPR-BAT.pdf>. Accessed: Jul. 21, 2016. doi:10.1016/j.jag.2016.07.016.
http://ipl.uv.es/artmo/files/Verrelst_et...
)).These methods have not been widely applied in machine learning until recently, due to their high computational complexity. The GPR is a family of kernel methods with the additional advantage of providing full conditional statistical descriptions for predicted variables, which are primarily used to establish confidence intervals and set hyper-parameters (RASMUSSEN & WILLIAMS, 2006RASMUSSEN, C., WILLIAMS, C. Gaussian processes for machine learning. MIT Press, 2006.). The system can be identified by searching relationships in the training data, which are suitable for the analysis of high-dimensional, small sample, and nonlinear problems. For any set of random variables {xi ϵ X, i = 1, 2, …, n}, the joint probability distribution of the process corresponds to states {Y(x1 ), Y(x2 ), …, Y(xn )}, which are subject to the n-dimensional Gaussian distribution. In function space, all statistical features for the Gaussian process are determined by its mean μ (x) and covariance functions C(x, x`) C(x, x`). These can be expressed as:
…(5)
Where x, x ϵ X are random input variables and d is a dimensional vector. The Gaussian process can then be defined as f(x)~GP(μ(x), C(x, x’)). A total of n data sets were used as the training sample D = {( x i , y i ), i = 1, 2, …, n} for the Gaussian process, where x i is the d-dimensional input vector and the observed target is denoted as y i ϵ R. Noise affected the observation of the target y and real output difference for ε. The standard linear regression model with Gaussian white noise can be expressed as:
… (6) where is a random noise-independent variable expressed as ε~N (0, ), where is the noise variance. The prior distribution of the target value x is given by:
…(7) where is I the identity matrix.
This Bayesian framework can be used in the functional space, defined by the GPR prior distribution, to calculate a posterior distribution of the function and predict its output value. The training sample output y and the test sample output y* were combined with the Gaussian prior distribution as follows:
…(8)
In this formula, C (X, X) is the covariance matrix of positive definite n x n order. The correlation between x i and x j is characterized by the arbitrary term c ij . The term C (X, x * ) represents the covariance matrix for the training set input X and the test set x * . The term C (x * , x * ) is the covariance of the test set x * .
The objective of GPR, given a known input x * and training set D, is to compute . The Bayesian probability of the posterior distribution is then given by:
…(9)
The predictive value of y * follows the normal distribution, with an expected value of μy * and a variance of . These can be expressed as:
,…(10)
…(11)
For a level of 1- α, the confidence interval for GPR probability prediction results is given by:
…(12), where Lb 1-α (y * ) and Ub 1-a (y * ) are the lower and upper bounds of the predictive values and Z (1-α)/2 is the quantile of the standard normal distribution.
RESULTS AND DISCUSSION:
Pure rice information acquisition
In addition to rice plants, fields include soil, water, and green algae which act as interference factors (see Fig. 3). It is necessary to classify and extract images to obtain pure hyperspectral information from rice, which is used for the subsequent inversion modeling. The SAM method was used in this study to classify hyperspectral data. Figure 4 demonstrates the viability of this technique as the rice can be easily separated from adjacent objects. This is because the average spectrum of known rice points was extracted from the image as a reference and the similarity between the two spectra was determined. The generalized angle was calculated between each pixel vector and the reference spectral vector in each hyperspectral image. This method assumes the image data have been reduced to ‘apparent reflectance,’ which implies all dark radiation and path radiation deviations have been removed.
Machine learning
The accuracy of the proposed GPR model was calculated using a linear fit and the root mean square error (RMSE), achieving values of R2=0.8525 and RMSE=0.9507. A comparison between the predicted and measured data is shown in figure 5. It is evident from the figure that this inversion effect is more accurate in the middle part of the nitrogen range.
Hyperspectral images have been used in prior studies to monitor rice growing conditions (SWAIN et al. (2010SWAIN, K.C. et al. Adoption of an unmanned helicopter for low-altitude remote sensing to estimate yield and total biomass of a rice crop. Transactions of the ASABE, v.53, p.21-27, 2010. Available from: https://naldc.nal.usda.gov/download/41029/PDF>. Accessed: May. 26, 2016,
https://naldc.nal.usda.gov/download/4102...
)). For example, Uto et al. (2013UTO, K. et al. Characterization of rice paddies by a UAV-mounted miniature hyperspectral sensor system. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6, 851-860, 2013. Available from: https://ieeexplore.ieee.org/document/6482672/>. Accessed: Mar. 16, 2017. doi: 10.1109/JSTARS.2013.2250921.
https://ieeexplore.ieee.org/document/648...
) developed a low-cost UAV sensor to estimate chlorophyll densities in plants with high accuracy (UTO et al. (2013UTO, K. et al. Characterization of rice paddies by a UAV-mounted miniature hyperspectral sensor system. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6, 851-860, 2013. Available from: https://ieeexplore.ieee.org/document/6482672/>. Accessed: Mar. 16, 2017. doi: 10.1109/JSTARS.2013.2250921.
https://ieeexplore.ieee.org/document/648...
)). Zhu et al. (2009ZHU, J. et al. Quantifying nitrogen status of rice using low altitude UAV-mounted system and object-oriented segmentation methodology. ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, p.603-609. ) used a low-altitude UAV and object-oriented segmentation to estimate nitrogen rates in rice crops (ZHU et al. (2009ZHU, J. et al. Quantifying nitrogen status of rice using low altitude UAV-mounted system and object-oriented segmentation methodology. ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, p.603-609. )). While GPR has been used previously for the monitoring of various rice plant parameters, such as LAI (CAMPOS-TABERNER et al. (2016CAMPOS-TABERNER, M. et al. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sensing of Environment, v.187, p.102-118, 2016. Available from: http://agri.ckcest.cn/ass/NK005-20170130005.pdf>. Accessed: Feb. 11, 2017. doi:10.1016/j.rse.2016.10.009.
http://agri.ckcest.cn/ass/NK005-20170130...
)), this study represents the first application of GPR specifically to measuring rice nitrogen content. The GPR was selected for this study, as opposed to more conventional techniques, because of its efficiency and accuracy.
Verrelst et al. (2012VERRELST, J. et al. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Transactions on Geoscience and Remote Sensing, v.50, p.1832-1843, 2012. Available from: https://www.mendeley.com/research-papers/retrieval-vegetation-biophysical-parameters-using-gaussian-process-techniques/>. Accessed: Nov. 18, 2016. doi:10.1109/TGRS.2011.2168962.
https://www.mendeley.com/research-papers...
) recently evaluated several parametric and non-parametric techniques for estimating vegetation parameters, using data from the hyperspectral Compact High-Resolution Imaging Spectrometer (CHRIS) (VERRELST et al. (2012VERRELST, J. et al. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Transactions on Geoscience and Remote Sensing, v.50, p.1832-1843, 2012. Available from: https://www.mendeley.com/research-papers/retrieval-vegetation-biophysical-parameters-using-gaussian-process-techniques/>. Accessed: Nov. 18, 2016. doi:10.1109/TGRS.2011.2168962.
https://www.mendeley.com/research-papers...
)). This comparison included conventional parametric techniques such as generic narrowband vegetation indices (VIs) and the normalized area over reflectance curve method. The GPR outperformed these other methods while including only 4 of the available 62 bands. This represents a significant decrease in data processing requirements, leading to increases in operational efficiency and reduced runtimes. The GPR has also been shown to provide higher estimation accuracy when compared with support vector regression (SVR), general regression neural networks, and band ratio polynomial regression (PASOLLI et al. (2010PASOLLI, L. et al. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geoscience and Remote Sensing Letters, v.7, p.464-468, 2010. Available from: https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005411816>. Accessed: Jul. 18, 2016. doi:10.1109%2FLGRS.2009.2039191.
https://www.infona.pl/resource/bwmeta1.e...
)). As discussed by Verrelst et al. (2013)VERRELST, J. et al. Gaussian process retrieval of chlorophyll content from imaging spectroscopy data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, v.6, p.867-874, 2013. Available from: https://www.mendeley.com/research-papers/gaussian-process-retrieval-chlorophyll-content-imaging-spectroscopy-data/>. Accessed: Jun. 28, 2017. doi: 10.1109/JSTARS.2012.2222356.
https://www.mendeley.com/research-papers...
, GPR algorithms are easier to train than neural networks and allow for more flexibility than support vector machines (SVMs) in the choice of kernel type (VERRELST et al. (2012)); ARENAS-GARCIA et al. (2013ARENAS-GARCIA, J. et al. Kernel Multivariate Analysis Framework for Supervised Subspace Learning: A Tutorial on Linear and Kernel Multivariate Methods. IEEE Signal Processing Magazine, v.30, p.16-29, 2013. Available from: http://sci-hub.tw/10.1109/msp.2013.2250591>. Accessed: Jun. 15, 2017. doi:10.1109/MSP.2013.2250591.
http://sci-hub.tw/10.1109/msp.2013.22505...
)). The utilization of dimensionality reduction further increased the efficiency of the proposed technique (MAATEN et al. (2007MAATEN, L.J.P.V.D. et al. Dimensionality Reduction: A Comparative Review. Journal of Machine Learning Research, v.10, 2007. Available from: https://core.ac.uk/display/23318387>. Accessed: May. 19, 2017. doi:10.1.1.364.6824.
https://core.ac.uk/display/23318387...
)), which has been demonstrated as a viable new tool for crop monitoring.
Results demonstrated the proposed SAM technique accurately extracted high-detail information from the acquired rice images. This is primarily because the spectral characteristics of plants differed significantly from those of adjacent water or soil. As is evident in Figure 5, the error between the measured and predicted values was larger at the boundary of the nitrogen range and smaller in the middle. Spectral bands in this study were located within a range of 400-1000nm. It is possible that the sensitive bands in this range may have been weak, resulting in relatively low inversion accuracy. In future research, the scope of this study will be broadened to include other wavelengths, as well as various sampling sights, terrain distributions, and crop types.
CONCLUSION:
In this study, a hyperspectral remote sensing platform was used to extract nitrogen content from a rice canopy. Machine learning based on Gaussian process regression was utilized to identify the most relevant spectral bands, thereby reducing noise and increasing inversion accuracy. Ground truth rice leaf nitrogen levels were obtained by invasive ground sampling and compared with information from the proposed inversion technique. Principal component analysis was used for dimensionality reduction to eliminate redundant spectral data, thereby increasing system efficiency. Results demonstrated the proposed spectral angle mapper could acquire accurate pure rice information from the original image. These processed data were used to establish a nitrogen inversion model, the accuracy of which was assessed using two metrics with resulting values of R2=0.8525 and RMSE=0.9507. This suggested that the proposed method could be a valuable new imaging tool for the non-invasive measurement of nitrogen nutrition levels in rice fields.
ACKNOWLEDGMENTS
This work was funded by National Key R&D Program of China and by Ministry of Science and Technology of the People’s Republic of China (2016YFD0200600 and 2016YFD0200603).We would like to thank the Liaoning Engineering Research Center for Information Technology in Agriculture for the use of their equipment.
REFERENCES:
- ADAM, E. et al. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: a review. Wetlands Ecology and Management, v.18, p.281-296, 2010. Available from: https://link.springer.com/article/10.100 7%2Fs11273-009-9169-z>. Accessed: Jun. 27, 2017. doi:10.1007/s11273-009-9169-z.
» https://doi.org/10.1007/s11273-009-9169-z» https://link.springer.com/article/10.100 7%2Fs11273-009-9169-z - AN, G. A. et al. Studies on the detemination of ammonia-nitrogen in water samples by BUCHI Kjeldahl line instrument. Modern Scientific Instruments, v.1, p.28-29, 2004. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xdkxyq200401010>. Accessed: May. 27, 2017. doi:10.3969/j.issn.1003-8892.2004.01.010.
» https://doi.org/10.3969/j.issn.1003-8892.2004.01.010» http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xdkxyq200401010 - ARENAS-GARCIA, J. et al. Kernel Multivariate Analysis Framework for Supervised Subspace Learning: A Tutorial on Linear and Kernel Multivariate Methods. IEEE Signal Processing Magazine, v.30, p.16-29, 2013. Available from: http://sci-hub.tw/10.1109/msp.2013.2250591>. Accessed: Jun. 15, 2017. doi:10.1109/MSP.2013.2250591.
» https://doi.org/0.1109/MSP.2013.2250591.» http://sci-hub.tw/10.1109/msp.2013.2250591 - CAMPOS-TABERNER, M. et al. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sensing of Environment, v.187, p.102-118, 2016. Available from: http://agri.ckcest.cn/ass/NK005-20170130005.pdf>. Accessed: Feb. 11, 2017. doi:10.1016/j.rse.2016.10.009.
» https://doi.org/10.1016/j.rse.2016.10.009» http://agri.ckcest.cn/ass/NK005-20170130005.pdf - CHEN, G.Y., QIAN, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Transactions on Geoscience and Remote Sensing, v.49, p.973-980, 2011. Available from: https://ieeexplore.ieee.org/document/5607305/>. Accessed: Jun. 10, 2017. doi:10.1109/TGRS.2010.2075937.
» https://doi.org/10.1109/TGRS.2010.2075937» https://ieeexplore.ieee.org/document/5607305/ - COLOMINA, I., MOLINA, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS Journal of Photogrammetry and Remote Sensing, v.92, p.79-97, 2014. Available from: https://zenodo.org/record/57983#.WyO_o0xuJPY>. Accessed: Sep. 17, 2016. doi:10.1016/j.isprsjprs.2014.02.013.
» https://doi.org/10.1016/j.isprsjprs.2014.02.013» https://zenodo.org/record/57983#.WyO_o0xuJPY - CÓRCOLES, J.I. et al. Estimation of leaf area index in onion (Allium cepa L.) using an unmanned aerial vehicle. Biosystems Engineering, v.115, p.31-42, 2013. Available from: https://www.sciencedirect.com/science/article/pii/S1537511013000214?via%3Dihub>. Accessed: Mar. 7, 2017. doi:10.1016/j.biosystemseng.2013.02.002.
» https://doi.org/10.1016/j.biosystemseng.2013.02.002» https://www.sciencedirect.com/science/article/pii/S1537511013000214?via%3Dihub - DU, W., XU, T.Y. Effect and assessment of UAV spraying parameters at japonica rice canopies. Journal of Agricultural Mechanization Research, v.4, p.182-186, 2017. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=njhyj201704036>. Accessed: May. 03, 2016. doi: 10.3969/j.issn.1003-188X.2017.04.036.
» https://doi.org/10.3969/j.issn.1003-188X.2017.04.036.» http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=njhyj201704036 - GARRIGUES, S. et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. Journal of Geophysical Research: Biogeosciences, v.113, 2008. Available from: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2007JG000635> . Accessed: Jul. 13, 2017. doi:10.1029/2007JG000635.
» https://doi.org/10.1029/2007JG000635» https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2007JG000635 - GOVENDER, M. et al. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa, v.33, p.145-151, 2007. Available from: http://www.oalib.com/paper/1350213#.WyPCUUxuJPY>. Accessed: Jan. 12, 2016. doi:10.4314/wsa.v33i2.49049.
» https://doi.org/10.4314/wsa.v33i2.49049» http://www.oalib.com/paper/1350213#.WyPCUUxuJPY - HOMOLOVÁ, L. et al. Review of optical-based remote sensing for plant trait mapping. Ecological Complexity, v.15, p.1-16, 2013. Available from: http://library.wur.nl/WebQuery/wurpubs/442967>. Accessed: May. 15, 2017. doi:10.1016/j.ecocom.2013.06.003.
» https://doi.org/10.1016/j.ecocom.2013.06.003» http://library.wur.nl/WebQuery/wurpubs/442967 - JOLLIFFE, I.T. Principal Component Analysis. Second Edition, New York: Springer, p.1-6, 2002.
- LAN, Y.B. Agricultural aviation applications in USA. Transactions of the Chinese Society for Agricultural Machinery, v.5, p.194-201, 2013. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=nyjxxb201305034>. Accessed: Apr. 14, 2017. doi:10.6041/j.issn.1000-1298.2013.05.034.
» https://doi.org/10.6041/j.issn.1000-1298.2013.05.034» http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=nyjxxb201305034 - LEE, Y.J. et al. A simple spectral index using reflectance of 735nm to assess nitrogen status of rice canopy. Agronomy Journal, v.100, p.205-212, 2008. Available from: https://dl.sciencesocieties.org/publications/aj/abstracts/100/1/205>. Accessed: Jan. 13, 2017. doi:10.2134/agronj2007.0018.
» https://doi.org/10.2134/agronj2007.0018» https://dl.sciencesocieties.org/publications/aj/abstracts/100/1/205 - LI, M. et al. A systematic comparison of different object-based classification techniques using high spatial resolution imagery in agricultural environments. International Journal of Applied Earth Observation and Geoinformation, v.49, p.87-98, 2016. Available from: http://agri.ckcest.cn/ass/NK005-20160328004.pdf>. Accessed: Mar. 24, 2016. doi: 10.1016/j.jag.2016.01.011.
» https://doi.org/10.1016/j.jag.2016.01.011.» http://agri.ckcest.cn/ass/NK005-20160328004.pdf - LIU, F. Study on monitoring fractional vegetation cover of garden plots by unmanned aerial vehicles. Transactions of the Chinese Society for Agriculural Machinery, v.45, p.250-257, 2014. Available from: http://www.wanfangdata.com.cn/details/detail.d o?_type=perio&id=nyjxxb201411039>. Accessed: Dec. 11, 2017. doi:10.6041/j.issn.1000-1298.2014.11.039.
» https://doi.org/0.6041/j.issn.1000-1298.2014.11.039.» http://www.wanfangdata.com.cn/details/detail.d o?_type=perio&id=nyjxxb201411039 - MAATEN, L.J.P.V.D. et al. Dimensionality Reduction: A Comparative Review. Journal of Machine Learning Research, v.10, 2007. Available from: https://core.ac.uk/display/23318387>. Accessed: May. 19, 2017. doi:10.1.1.364.6824.
» https://doi.org/10.1.1.364.6824» https://core.ac.uk/display/23318387 - MULLA, D.J. Twenty-five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosystems engineering, v.114, p.358-371, 2013. Available from: http://ccc.inaoep.mx/~mdprl/documentos/17062015.pdf>. Accessed: May. 20, 2016. Doi:10.1016/j.jag.2016.01.011.
» https://doi.org/0.1016/j.jag.2016.01.011.» http://ccc.inaoep.mx/~mdprl/documentos/17062015.pdf - PASOLLI, L. et al. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geoscience and Remote Sensing Letters, v.7, p.464-468, 2010. Available from: https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005411816>. Accessed: Jul. 18, 2016. doi:10.1109%2FLGRS.2009.2039191.
» https://doi.org/10.1109%2FLGRS.2009.2039191» https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005411816 - RASMUSSEN, C., WILLIAMS, C. Gaussian processes for machine learning. MIT Press, 2006.
- SANKARAN, S. et al. Field-based crop phenotyping: Multispectral aerial imaging for evaluation of winter wheat emergence and spring stand. Computers and Electronics in Agriculture, v.118, p.372-379, 2015. Available from: https://www.sciencedirect. com/science/article/pii/S0168169915002768>. Accessed: May. 15, 2017, doi:10.1016/j.compag.2 015.09.001.
» https://doi.org/10.1016/j.compag.2 015.09.001» https://www.sciencedirect. com/science/article/pii/S0168169915002768 - SCHAEPMAN, M. E. et al. Earth system science related imaging spectroscopy-an assessment. Remote Sens. Environ, v.113, p.123-137, 2009. Available from: https://www.sciencedirect.com/science/article/pii/S0034425709000819>. Accessed: Mar. 02, 2017, doi:10.1016/j.rse.2009.03.001.
» https://doi.org/10.1016/j.rse.2009.03.001» https://www.sciencedirect.com/science/article/pii/S0034425709000819 - SEVERTSON, D. et al. Unmanned aerial vehicle canopy reflectance data detects potassium deficiency and green peach aphid susceptibility in canola. Precision Agriculture, p.1-19 2016. Available from: https://link.springer.com/article/10.1007%2Fs11119-016-9442-0>. Accessed: Jul. 20, 2016 doi:10.1007/s11119-016-9442-0.
» https://doi.org/10.1007/s11119-016-9442-0» https://link.springer.com/article/10.1007%2Fs11119-016-9442-0 - SHLENS, J. A tutorial on principal component analysis. New York: Cornell University, 2002.
- SUGIURA, R. et al. Remote-sensing technology for vegetation monitoring using an unmanned helicopter. Biosystems Engineering , v.90, p.369-379, 2005. Available from: http://elibrary.asabe.org/abstract.asp?aid=17837>. Accessed: Sep. 15, 2017. doi: 10.13031/2013.1 7837.
» https://doi.org/10.13031/2013.1 7837.» http://elibrary.asabe.org/abstract.asp?aid=17837 - SWAIN, K.C. et al. Adoption of an unmanned helicopter for low-altitude remote sensing to estimate yield and total biomass of a rice crop. Transactions of the ASABE, v.53, p.21-27, 2010. Available from: https://naldc.nal.usda.gov/download/41029/PDF>. Accessed: May. 26, 2016,
» https://naldc.nal.usda.gov/download/41029/PDF - TAERYON, C. Alternative posterior consistency results in nonparametric binaryregression using Gaussian process priors. Journal of Statistical Planning and Inference, v.137, p.2975-2983, 2007. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0378375807000407>. Accessed: Sep. 26, 2017. doi:10.1016/j.jspi.2006.11.001.
» https://doi.org/10.1016/j.jspi.2006.11.001» https://linkinghub.elsevier.com/retrieve/pii/S0378375807000407 - USTIN, S., GAMON, J. Remote sensing of plant functional types. New Phytologist, v.186, p.795-816, 2010. Available from: https://www.ncbi.nlm.nih.gov/pubmed/20569415>. Accessed: Apr. 22, 2016. doi:10.1111/j.1469-8137.2010.03284.x.
» https://doi.org/10.1111/j.1469-8137.2010.03284.x.» https://www.ncbi.nlm.nih.gov/pubmed/20569415 - UTO, K. et al. Characterization of rice paddies by a UAV-mounted miniature hyperspectral sensor system. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6, 851-860, 2013. Available from: https://ieeexplore.ieee.org/document/6482672/>. Accessed: Mar. 16, 2017. doi: 10.1109/JSTARS.2013.2250921.
» https://doi.org/10.1109/JSTARS.2013.2250921.» https://ieeexplore.ieee.org/document/6482672/ - VERRELST, J. et al. Gaussian process retrieval of chlorophyll content from imaging spectroscopy data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, v.6, p.867-874, 2013. Available from: https://www.mendeley.com/research-papers/gaussian-process-retrieval-chlorophyll-content-imaging-spectroscopy-data/>. Accessed: Jun. 28, 2017. doi: 10.1109/JSTARS.2012.2222356.
» https://doi.org/10.1109/JSTARS.2012.2222356.» https://www.mendeley.com/research-papers/gaussian-process-retrieval-chlorophyll-content-imaging-spectroscopy-data/ - VERRELST, J. et al. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Transactions on Geoscience and Remote Sensing, v.50, p.1832-1843, 2012. Available from: https://www.mendeley.com/research-papers/retrieval-vegetation-biophysical-parameters-using-gaussian-process-techniques/>. Accessed: Nov. 18, 2016. doi:10.1109/TGRS.2011.2168962.
» https://doi.org/10.1109/TGRS.2011.2168962» https://www.mendeley.com/research-papers/retrieval-vegetation-biophysical-parameters-using-gaussian-process-techniques/ - VERRELST, J. et al. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. International Journal of Applied Earth Observation and Geoinformation, v.52, p.554-567, 2016. Available from: http://ipl.uv.es/artmo/files/Verrelst_etal2016_GPR-BAT.pdf>. Accessed: Jul. 21, 2016. doi:10.1016/j.jag.2016.07.016.
» https://doi.org/10.1016/j.jag.2016.07.016» http://ipl.uv.es/artmo/files/Verrelst_etal2016_GPR-BAT.pdf - WANG, J.N. et al. Effects of N, P, K Fertilizer application on grain yield, quality, nutrient uptake and utilization of rice. Chinese Journal of Rice Science, v.6, p.645-653, 2011. Available from: http://en.cnki.com.cn/Article_en/CJFDTotal-ZGSK201106013.htm>. Accessed: Nov. 25, 2017. doi:10.3969/j.issn.1001-7216.2011.06.012.
» https://doi.org/10.3969/j.issn.1001-7216.2011.06.012» http://en.cnki.com.cn/Article_en/CJFDTotal-ZGSK201106013.htm - WANG, P., LUO, X.W. Key technology for remote sensing information acquisition based on micro UAV. Transactions of the Chinese Society of Agricultural Engineering, v.18, p.1-12, 2014. Available from: http://www.ingentaconnect.com/content/tcsae/tcsae/2014/00000030/000000.18/art00001#>. Accessed: Jun. 12, 2016. doi: 10.3969/j.issn.1002-6819.2014.18.001.
» https://doi.org/10.3969/j.issn.1002-6819.2014.18.001.» http://www.ingentaconnect.com/content/tcsae/tcsae/2014/00000030/000000.18/art00001# - WATTS, A.C. et al. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sensing, v.4, p.1671-1692, 2012. Available from: http://www.mdpi.com/2072-4292/4/6/1671>. Accessed: Jul. 14, 2017. doi:10.3390/rs4061671.
» https://doi.org/1671-1692» https://doi.org/10.3390/rs4061671» http://www.mdpi.com/2072-4292/4/6/1671 - YU, F.H., XU, T.Y. Models for estimating the leaf NDVI of japonica rice on a canopy scale by combining canopy NDVI and multisource environmental data in Northeast China. International Journal of Agricultural and Biology, v.9, p.132-142, 2016. Available from: https://ijabe.org/index.php/ijabe/article/view/2266>. Accessed: Feb. 09, 2017. doi:10.3965/j.ijabe.20160905.2266.
» https://doi.org/10.3965/j.ijabe.20160905.2266» https://ijabe.org/index.php/ijabe/article/view/2266 - ZAMAN-ALLAH, M. et al. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant methods, v.11, p.35, 2015. Available from: https://plantmethods.biomedcentral.com/articles/10.1186/s13007-015-0078-2>. Accessed: Feb. 18, 2016. doi:10.1186/s13007-015-0078-2.
» https://doi.org/10.1186/s13007-015-0078-2» https://plantmethods.biomedcentral.com/articles/10.1186/s13007-015-0078-2 - ZENG, L. et al. Compressed sensing based speech spare representation with KL expansion. Journal of Data Acquisition and Processing, v.3, p.267-273, 2013. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjcjycl201303002>. Accessed: Nov. 19, 2017. doi:10.3969/j.issn.1004-9037.2013.03.002.
» https://doi.org/10.3969/j.issn.1004-9037.2013.03.002» http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjcjycl201303002 - ZHAO, F. et al. An image algorithm based on singular value decomposition. Journal of Computer Research and Development, v.47, p.23-32, 2015. Available from: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyjyfz201001004>. Accessed: Dec. 23, 2016.
» http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyjyfz201001004 - ZHU, J. et al. Quantifying nitrogen status of rice using low altitude UAV-mounted system and object-oriented segmentation methodology. ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, p.603-609.
-
0
CR-2018-0008.R2
Publication Dates
-
Publication in this collection
2018
History
-
Received
08 Jan 2018 -
Accepted
30 May 2018 -
Reviewed
27 June 2018